
Euler brick
Encyclopedia
In mathematics
, an Euler brick, named after Leonhard Euler
, is a cuboid
whose edges
and face diagonal
s all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime.
s: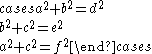
Euler found at least two parametric solutions to the problem, but neither give all solutions.
Given an Euler brick with edges (a, b, c), the triple (bc, ac, ab) constitutes an Euler brick as well.
 and face diagonals 267, 244, and 125.
and face diagonals 267, 244, and 125.
Other solutions are: Given as: length (a, b, c)
is also an integer.
In other words the following equation is added to the above Diophantine equation
s:
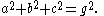
Some interesting facts about a primitive perfect cuboid:
As of January 2011, no example of a perfect cuboid had been found and no one had proven that it cannot exist. Exhaustive computer searches show that, if a perfect cuboid exists, one of its sides must be greater than 1 trillion (1012).
Solutions have been found where the space diagonal and two of the three face diagonals are integers, such as: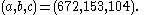
Solutions are also known where all four diagonals but only two of the three edges are integers, such as:
and
with all right angles. In 2009, a perfect parallelepiped was shown to exist, answering an open question of Richard Guy
. Solutions with only a single oblique angle have been found.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Euler brick, named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, is a cuboid
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
whose edges
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
and face diagonal
Face diagonal
In geometry, a face diagonal of a polyhedron is a diagonal on one of the faces, in contrast to a space diagonal passing through the interior of the polyhedron....
s all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime.
Properties
Alternatively stated, an Euler brick is a solution to the following system of Diophantine equationDiophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s:
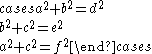
Euler found at least two parametric solutions to the problem, but neither give all solutions.
Given an Euler brick with edges (a, b, c), the triple (bc, ac, ab) constitutes an Euler brick as well.
Examples
The smallest Euler brick, discovered by Paul Halcke in 1719, has edges and face diagonals 267, 244, and 125.
and face diagonals 267, 244, and 125.Other solutions are: Given as: length (a, b, c)
- (275, 252, 240),
- (693, 480, 140),
- (720, 132, 85), and
- (792, 231, 160).
Perfect cuboid
A perfect cuboid (also called a perfect box) is an Euler brick whose space diagonalSpace diagonal
In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner...
is also an integer.
In other words the following equation is added to the above Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s:
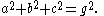
Some interesting facts about a primitive perfect cuboid:
- 2 of the edges {a,b,c} must be even and 1 edge must be odd
- 1 edge must be divisible by 4 and 1 edge must be divisible by 16
- 1 edge must be divisible by 3 and 1 edge must be divisible by 9
- 1 edge must be divisible by 5
- 1 edge must be divisible by 7
- 1 edge must be divisible by 11
- 1 edge must be divisible by 19.
As of January 2011, no example of a perfect cuboid had been found and no one had proven that it cannot exist. Exhaustive computer searches show that, if a perfect cuboid exists, one of its sides must be greater than 1 trillion (1012).
Solutions have been found where the space diagonal and two of the three face diagonals are integers, such as:
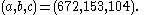
Solutions are also known where all four diagonals but only two of the three edges are integers, such as:

and

Perfect parallelepiped
A perfect cuboid is the special case of a perfect parallelepipedParallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
with all right angles. In 2009, a perfect parallelepiped was shown to exist, answering an open question of Richard Guy
Richard K. Guy
Richard Kenneth Guy is a British mathematician, Professor Emeritus in the Department of Mathematics at the University of Calgary....
. Solutions with only a single oblique angle have been found.

