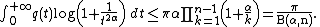Khabibullin’s conjecture on integral inequalities
Encyclopedia
In mathematics, Khabibullin's conjecture, named after B. N. Khabibullin, is related to Paley
's problem for plurisubharmonic functions and to various extremal problems in the theory of entire function
s of several variables.
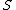 be a non-negative increasing function on the half-line
be a non-negative increasing function on the half-line 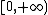 such that
such that  . Assume that
. Assume that 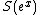 is a convex function of
is a convex function of 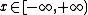 . Let
. Let 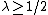 ,
, 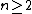 , and
, and 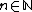 . If
. If
then
This statement of the Khabibullin's conjecture completes his survey.
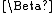 :
: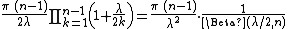
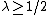 the function
the function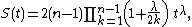
turns the inequalities and to
equalities.
The Khabibullin's conjecture is valid for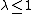 without the assumption of convexity of
without the assumption of convexity of 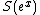 . Meanwhile, one can show that this conjecture is not valid without some convexity conditions for
. Meanwhile, one can show that this conjecture is not valid without some convexity conditions for 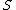 . Nowadays it is even unknown if the conjecture is true for
. Nowadays it is even unknown if the conjecture is true for  and for at least one
and for at least one
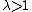 .
.
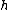 be a non-negative increasing function on the half-line
be a non-negative increasing function on the half-line  and
and 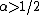 . If
. If
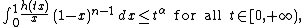
then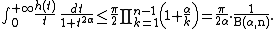
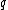 be a non-negative continuous function on the half-line
be a non-negative continuous function on the half-line  and
and 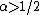 . If
. If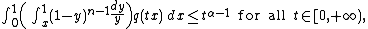
then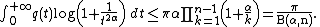
Raymond Paley
Raymond Edward Alan Christopher Paley was an English mathematician. Paley was born in Bournemouth, England. He was educated at Eton. From there he entered Trinity College, Cambridge where he showed himself the most brilliant student among a remarkable collection of fellow undergraduates...
's problem for plurisubharmonic functions and to various extremal problems in the theory of entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s of several variables.
The first statement in terms of logarithmically convex functions
Khabibullin's conjecture (version 1, 1992). Let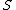 be a non-negative increasing function on the half-line
be a non-negative increasing function on the half-line 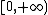 such that
such that  . Assume that
. Assume that 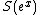 is a convex function of
is a convex function of 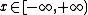 . Let
. Let 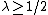 ,
, 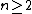 , and
, and 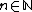 . If
. Ifthen
This statement of the Khabibullin's conjecture completes his survey.
Relation to Euler's Beta function
Note that the product in the right hand side of the inequality is related to the Euler's Beta function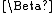 :
: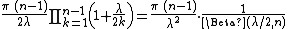
Discussion
For each fixed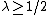 the function
the function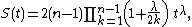
turns the inequalities and to
equalities.
The Khabibullin's conjecture is valid for
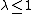 without the assumption of convexity of
without the assumption of convexity of 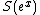 . Meanwhile, one can show that this conjecture is not valid without some convexity conditions for
. Meanwhile, one can show that this conjecture is not valid without some convexity conditions for 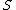 . Nowadays it is even unknown if the conjecture is true for
. Nowadays it is even unknown if the conjecture is true for  and for at least one
and for at least one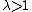 .
.The second statement in terms of increasing functions
Khabibullin's conjecture (version 2). Let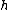 be a non-negative increasing function on the half-line
be a non-negative increasing function on the half-line  and
and 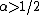 . If
. If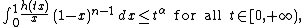
then
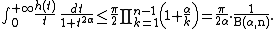
The third statement in terms of non-negative functions
Khabibullin's conjecture (version 3). Let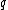 be a non-negative continuous function on the half-line
be a non-negative continuous function on the half-line  and
and 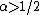 . If
. If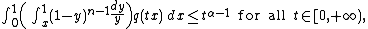
then