Circular law
Encyclopedia
In probability theory
, more specifically the study of random matrices, the circular law describes the distribution of eigenvalues of an
random matrix
with independent and identically distributed entries
in the limit
.
It asserts that for any sequence of random
matrices whose entries are independent and identically distributed random variables
, all with mean
zero and variance
equal to 1/n, the limiting spectral distribution is the uniform distribution
over the unit disc.
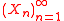be a sequence of 
matrix ensembles whose entries are i.i.d.
copies of a complex random variable
with mean
0 and variance
1. Let
denote the eigenvalues of 
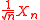. Define the empirical spectral measure of 
as
.
With these definitions in mind, the circular law asserts the sequence
converges weakly in distribution to the uniform measure on the unit disk.
. In the 1980s, Vyacheslav Girko introduced an approach which allowed to establish the circular law for more general distributions. Further progress was made by Zhidong Bai, who established the circular law under certain smoothness assumptions on the distribution.
The assumptions were further relaxed in the works of Terence Tao
and Van H. Vu
, Friedrich Götze and Alexander Tikhomirov. Finally, in 2010 Tao and Vu proved the circular law under the minimal assumptions stated above.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, more specifically the study of random matrices, the circular law describes the distribution of eigenvalues of an
random matrixRandom matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
with independent and identically distributed entries
Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
in the limit
.It asserts that for any sequence of random
matrices whose entries are independent and identically distributed random variablesIndependent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
, all with mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
zero and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
equal to 1/n, the limiting spectral distribution is the uniform distribution
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
over the unit disc.
Precise statement
Let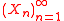 be a sequence of matrix ensembles whose entries are i.i.d.Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
copies of a complex random variable
with meanExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
0 and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
1. Let
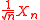denote the eigenvalues of . Define the empirical spectral measure of as.With these definitions in mind, the circular law asserts the sequence
converges weakly in distribution to the uniform measure on the unit disk.History
For random matrices with Gaussian distribution of entries (the Ginibre ensembles), the circular law was established in the 1960-s by Jean GinibreJean Ginibre
Jean Ginibre is a French mathematical physicist, known in particular for his contributions to random matrix theory , statistical mechanics , and partial differential equations. He received the Paul Langevin Prize in 1969.Jean Ginibre is Emeritus Professor at Paris-Sud 11 University....
. In the 1980s, Vyacheslav Girko introduced an approach which allowed to establish the circular law for more general distributions. Further progress was made by Zhidong Bai, who established the circular law under certain smoothness assumptions on the distribution.
The assumptions were further relaxed in the works of Terence Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
and Van H. Vu
Van H. Vu
Van H. Vu is a Vietnamese mathematician, a professor of mathematics at Yale University and the 2008 winner of the Pólya Prize of the Society for Industrial and Applied Mathematics for his work on concentration of measure. He is a collaborator of Terence Tao....
, Friedrich Götze and Alexander Tikhomirov. Finally, in 2010 Tao and Vu proved the circular law under the minimal assumptions stated above.