
Supercompact cardinal
Encyclopedia
In set theory
, a supercompact cardinal is a type of large cardinal. They display a variety of reflection properties.
, κ is λ-supercompact means that there exists an elementary embedding j from the universe V into a transitive inner model
M with critical point
κ, j(κ)>λ and
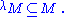
That is, M contains all of its λ-sequences. Then κ is supercompact means that it is λ-supercompact for all ordinals λ.
Alternatively, an uncountable cardinal κ is supercompact if for every A such that |A| ≥ κ there exists a normal measure
over [A]< κ.
[A]< κ is defined as follows:

Finding a canonical inner model for supercompact cardinals is one of the major problems of inner model theory
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a supercompact cardinal is a type of large cardinal. They display a variety of reflection properties.
Formal definition
If λ is any ordinalOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, κ is λ-supercompact means that there exists an elementary embedding j from the universe V into a transitive inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
M with critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
κ, j(κ)>λ and
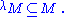
That is, M contains all of its λ-sequences. Then κ is supercompact means that it is λ-supercompact for all ordinals λ.
Alternatively, an uncountable cardinal κ is supercompact if for every A such that |A| ≥ κ there exists a normal measure
Normal measure
In set theory, a normal measure is a measure on a measurable cardinal κ such that the equivalence class of the identity function on κ maps to κ itself in the ultrapower construction...
over [A]< κ.
[A]< κ is defined as follows:

Properties
Supercompact cardinals have reflection properties. If a cardinal with some property (say a 3-huge cardinal) that is witnessed by a structure of limited rank exists above a supercompact cardinal κ, then a cardinal with that property exists below κ. For example, if κ is supercompact and the Generalized Continuum Hypothesis holds below κ then it holds everywhere because a bijection between the powerset of ν and a cardinal at least ν++ would be a witness of limited rank for the failure of GCH at ν so it would also have to exist below κ.Finding a canonical inner model for supercompact cardinals is one of the major problems of inner model theory
Inner model theory
In set theory, inner model theory is the study of certain models of ZFC or some fragment or strengthening thereof. Ordinarily these models are transitive subsets or subclasses of the von Neumann universe V, or sometimes of a generic extension of V. Inner model theory studies the relationships of...
.

