
Jacobian conjecture
Encyclopedia
In mathematics
, the Jacobian conjecture is a celebrated problem on polynomial
s in several variables
. It was first posed in 1939 by Ott-Heinrich Keller
. It was later named and widely publicised by Shreeram Abhyankar, as an example of a question in the area of algebraic geometry
that requires little beyond a knowledge of calculus
to state.
The Jacobian conjecture is notorious for the large number of attempted proofs that turned out to contain subtle errors. As of 2011, there are no plausible claims to have proved it.
and with coefficient
s in an algebraically closed field
k (in fact, it suffices to assume k=C, the field of complex number
s). We consider these as a single vector-valued function
whose components are the Fi.
The Jacobian determinant J of F is by definition the determinant
of the N × N matrix
consisting of the partial derivative
s of Fi with respect to Xj:
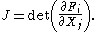
J is itself a function of the N variables X1, …, XN; indeed it is a polynomial function.
The condition
enters into the inverse function theorem
in multivariable calculus
. In fact that condition for smooth functions (and so in particular for polynomials) ensures the existence of a local inverse function to F, at any point where it holds.
Since k is algebraically closed and J is a polynomial, J will be zero for some complex values of X1, …, XN, unless we have the condition
Therefore it is a relatively elementary fact that
The Jacobian conjecture is a strengthening of the converse: it states that
2, and showed that the general case follows from the special case where the polynomials are of degree 3. checked the conjecture for polynomials of degree at most 100 in 2 variables.
The Jacobian conjecture is equivalent to the Dixmier conjecture
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Jacobian conjecture is a celebrated problem on polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in several variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. It was first posed in 1939 by Ott-Heinrich Keller
Ott-Heinrich Keller
Eduard Ott-Heinrich Keller was a German mathematician who worked in the fields of geometry, topology and algebraic geometry. He formulated the celebrated problem which is now called the Jacobian conjecture in 1939.He was born in Frankfurt–am-Main, and studied at the universities of Frankfurt,...
. It was later named and widely publicised by Shreeram Abhyankar, as an example of a question in the area of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
that requires little beyond a knowledge of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
to state.
The Jacobian conjecture is notorious for the large number of attempted proofs that turned out to contain subtle errors. As of 2011, there are no plausible claims to have proved it.
Formulation
For fixed N > 1 consider N polynomials Fi for 1 ≤ i ≤ N in the variables- X1, …, XN,
and with coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s in an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
k (in fact, it suffices to assume k=C, the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s). We consider these as a single vector-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
- F: kN → kN
whose components are the Fi.
The Jacobian determinant J of F is by definition the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the N × N matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
consisting of the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of Fi with respect to Xj:
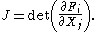
J is itself a function of the N variables X1, …, XN; indeed it is a polynomial function.
The condition
- J ≠ 0
enters into the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
in multivariable calculus
Multivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
. In fact that condition for smooth functions (and so in particular for polynomials) ensures the existence of a local inverse function to F, at any point where it holds.
Since k is algebraically closed and J is a polynomial, J will be zero for some complex values of X1, …, XN, unless we have the condition
- J is a constantConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
.
Therefore it is a relatively elementary fact that
- if F has an inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
G:kN → kN, then J is a non-zero constant.
The Jacobian conjecture is a strengthening of the converse: it states that
- if J is a non-zero constant, then F has an inverse function G:kN → kN, and G is regularRegular map (algebraic geometry)In algebraic geometry, a regular map between affine varieties is a mapping which is given by polynomials. For example, if X and Y are subvarieties of An resp...
(in the sense that its components are given by polynomial expressions).
Results
proved the Jacobian conjecture for polynomials of degreeDegree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
2, and showed that the general case follows from the special case where the polynomials are of degree 3. checked the conjecture for polynomials of degree at most 100 in 2 variables.
The Jacobian conjecture is equivalent to the Dixmier conjecture
Dixmier conjecture
In algebra the Dixmier conjecture, asked by , is the conjecture that any endomorphism of a Weyl algebra is an automorphism. showed that the Dixmier conjecture is equivalent to the Jacobian conjecture....
.

