In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, the unproven Erdős–Gyárfás conjecture, made in 1995 by the prolific mathematician Paul Erdős

Paul Erdos

Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...

 and his collaborator András Gyárfás

András Gyárfás

András Gyárfás is a Hungarian mathematician who specializes in combinatorics and graph theory. His Erdős number is 1.-External links:* at the Computer and Automation Research Institute, Hungarian Academy of Sciences*...

, states that any graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 with minimum degree 3 contains a simple cycle

Cycle (graph theory)

In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...

 whose length is a power of two

Power of two

In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....

. Erdős offered a prize of $100 for proving the conjecture, or $50 for a counterexample; it is one of many conjectures of Erdős

Erdos conjecture

The prolific mathematician Paul Erdős and his various collaborators made many famous mathematical conjectures, over a wide field of subjects.Some of these are the following:* The Cameron–Erdős conjecture on sum-free sets of integers, proved by Ben Green....

.

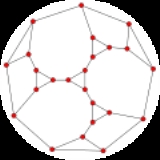
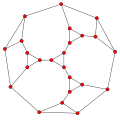
If the conjecture is false, a counterexample would take the form of a graph with minimum degree three having no power-of-two cycles. It is known through computer searches of Gordon Royle

Gordon Royle

Gordon F. Royle is a Professor at the School of Mathematics and Statistics at The University of Western Australia. He is well known for his research into the mathematics of Sudoku and his search for the Sudoku puzzle with the smallest number of entries that has a unique solution.-See...

 and Klas Markström that any counterexample must have at least 17 vertices, and any cubic

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

 counterexample must have at least 30 vertices. Markström's searches found four graphs on 24 vertices in which the only power-of-two cycles have 16 vertices; one of these four graphs is planar

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

.

Weaker results relating the degree of a graph to unavoidable sets of cycle lengths are known: there is a set S of lengths, with |S| = O(n^0.99), such that every graph with average degree ten or more contains a cycle with its length in S , and every graph whose average degree is exponential in the iterated logarithm

Iterated logarithm

In computer science, the iterated logarithm of n, written  n , is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1...

 of n necessarily contains a cycle whose length is a power of two . The conjecture is also known to be true for planar claw-free graphs and for graphs that avoid large induced star

Star (graph theory)

In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...

s and satisfy additional constraints on their degrees .