
K-set (geometry)
Encyclopedia

Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, a k-set of a finite point set S in the Euclidean plane is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of k elements of S that can be strictly separated from the remaining points by a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
. More generally, in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of higher dimensions, a k-set of a finite point set is a subset of k elements that can be separated from the remaining points by a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
. In particular, when k = n/2 (where n is the size of S), the line or hyperplane that separates a k-set from the rest of S is a halving line or halving plane.
K-sets are related by projective duality to k-levels in line arrangements
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
; the k-level in an arrangement of n lines in the plane is the curve consisting of the points that lie on one of the lines and have exactly k lines below them. Discrete and computational geometers have also studied levels in arrangements of more general kinds of curves and surfaces.
Combinatorial bounds
It is of importance in the analysis of geometric algorithms to bound the number of k-sets of a planar point set, or equivalently the number of k-levels of a planar line arrangement, a problem first studied by LovászLászló Lovász
László Lovász is a Hungarian mathematician, best known for his work in combinatorics, for which he was awarded the Wolf Prize and the Knuth Prize in 1999, and the Kyoto Prize in 2010....
(1971) and Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
et al. (1973). The best known upper bound for this problem is O(nk1/3), as was shown by Tamal Dey (1998) using the crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
inequality of Ajtai, Chvátal
Václav Chvátal
Václav Chvátal is a professor in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Canada, where he holds theCanada Research Chair in Combinatorial Optimization....
, Newborn, and Szemerédi
Endre Szemerédi
Endre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
. However, the best known lower bound is far from Dey's upper bound: it is Ω(n exp(c (logk)1/2)) for some constant c, as shown by Toth (2001).
In three dimensions, the best upper bound known is O(nk3/2), and the best lower bound known is Ω(nk exp(c (logk)1/2)).
For points in three dimensions that are in convex position, that is, are the vertices of some convex polytope, the number of k-sets is
Θ((n-k)k), which follows from arguments used for bounding the complexity of k-th order Voronoi diagrams.
For the case when k = n/2 (halving lines), the maximum number of combinatorially distinct lines through two points of S that bisect the remaining points when k = 1, 2, ... is
- 1,3,6,9,13,18,22... .
Bounds have also been proven on the number of ≤k-sets, where a ≤k-set is a j-set for some j ≤ k. In two dimensions, the maximum number of ≤k-sets is exactly nk, while in d dimensions the bound is
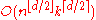 .
.Construction algorithms
Edelsbrunner and Welzl (1986) first studied the problem of constructing all k-sets of an input point set, or dually of constructing the k-level of an arrangement. The k-level version of their algorithm can be viewed as a plane sweep algorithm that constructs the level in left-to-right order. Viewed in terms of k-sets of point sets, their algorithm maintains a dynamic convex hullDynamic convex hull
The dynamic convex hull problem is a class of dynamic problems in computational geometry. The problem consists in the maintenance, i.e., keeping track, of the convex hull for the dynamically changing input data, i.e., when input data elements may be inserted, deleted, or modified...
for the points on each side of a separating line, repeatedly finds a bitangent
Bitangent
In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
of these two hulls, and moves each of the two points of tangency to the opposite hull. Chan (1999) surveys subsequent results on this problem, and shows that it can be solved in time proportional to Dey's O(nk1/3) bound on the complexity of the k-level.
Agarwal and Matoušek
Jirí Matoušek (mathematician)
Jiří Matoušek is a Czech mathematician working in computational geometry. He is a professor at Charles University in Prague and is the author of several textbooks and research monographs....
describe algorithms for efficiently constructing an approximate level; that is, a curve that passes between the (k - d)-level and the (k + d)-level for some small approximation parameter d. They show that such an approximation can be found, consisting of a number of line segments that depends only on n/d and not on n or k.
Matroid generalizations
The planar k-level problem can be generalized to one of parametric optimization in a matroidMatroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
: one is given a matroid in which each element is weighted by a linear function of a parameter λ, and must find the minimum weight basis of the matroid for each possible value of λ. If one graphs the weight functions as lines in a plane, the k-level of the arrangement of these lines graphs as a function of λ the weight of the largest element in an optimal basis in a uniform matroid, and Dey showed that his O(nk1/3) bound on the complexity of the k-level could be generalized to count the number of distinct optimal bases of any matroid with n elements and rank k.
For instance, the same O(nk1/3) upper bound holds for counting the number of different minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
s formed in a graph with n edges and k vertices, when the edges have weights that vary linearly with a parameter λ. This parametric minimum spanning tree problem has been studied by various authors and can be used to solve other bicriterion spanning tree optimization problems.
However, the best known lower bound for the parametric minimum spanning tree problem is Ω(n α(k)), where α is the inverse Ackermann function, an even weaker bound than that for the k-set problem. For more general matroids, Dey's O(nk1/3) upper bound has a matching lower bound.

