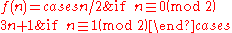Collatz conjecture - AbsoluteAstronomy.com

The Collatz conjecture is a conjecture

Conjecture

A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...

in mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

named after Lothar Collatz

Lothar Collatz

Lothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....

, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani

Shizuo Kakutani

was a Japanese-born American mathematician, best known for his eponymous fixed-point theorem.Kakutani attended Tohoku University in Sendai, where his advisor was Tatsujirō Shimizu. Early in his career he spent two years at the Institute for Advanced Study in Princeton at the invitation of the...

), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse

Helmut Hasse

Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...

), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers, or as wondrous numbers.

Take any natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

n. If n is even, divide it by 2 to get n / 2, if n is odd multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called "Half Or Triple Plus One", or HOTPO) indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1. The property has also been called oneness.

Paul Erdős

Paul Erdos

Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...

said, allegedly, about the Collatz conjecture: "Mathematics is not yet ripe for such problems" and also offered $500 for its solution.

In 2007, researchers Kurtz and Simon, building on earlier work by J.H. Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

in the 1970s,

The Collatz conjecture is a conjecture

Conjecture

in mathematics

Mathematics

named after Lothar Collatz

Lothar Collatz

Lothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....

, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani

Shizuo Kakutani

), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse

Helmut Hasse

), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers, or as wondrous numbers.

Take any natural number

Natural number

Paul Erdos

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

in the 1970s,

The Collatz conjecture is a conjecture

Conjecture

in mathematics

Mathematics

named after Lothar Collatz

Lothar Collatz

Lothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....

, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani

Shizuo Kakutani

), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse

Helmut Hasse

), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers, or as wondrous numbers.

Take any natural number

Natural number

Paul Erdos

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

in the 1970s, proved that a natural generalization of the Collatz problem is algorithmically undecidable

Undecidable problem

In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....

.
However, as this proof depends upon the generalization, it cannot be applied to the original Collatz problem.

Statement of the problem

Consider the following operation on an arbitrary positive integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

If the number is even, divide it by two.
If the number is odd, triple it and add one.

In modular arithmetic

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

notation, define the function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

f as follows:

Now, form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next.

In notation:

(that is:

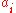is the value of

applied to

recursively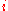

times;

)

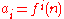or

(which yields

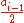for even

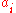and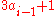

for odd

).

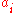The Collatz conjecture is: This process will eventually reach the number 1, regardless of which positive integer is chosen initially.

That smallest i such that a_i = 1 is called the total stopping time of n. The conjecture asserts that every n has a well-defined total stopping time. If, for some n, such an i doesn't exist, we say that n has infinite total stopping time and the conjecture is false.

If the conjecture is false, it can only be because there is some starting number which gives rise to a sequence which does not contain 1. Such a sequence might enter a repeating cycle that excludes 1, or increase without bound. No such sequence has been found.

Examples

For instance, starting with n = 6, one gets the sequence 6, 3, 10, 5, 16, 8, 4, 2, 1.

n = 11, for example, takes longer to reach 1: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

The sequence for n = 27, listed and graphed below, takes 111 steps, peaking at 9232 before descending to 1.

{ 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 }

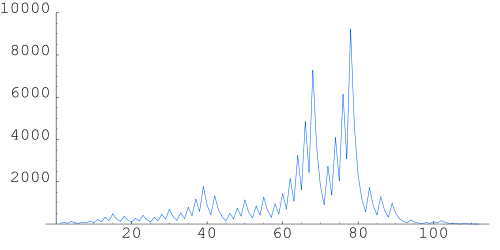
Numbers with a total stopping time longer than any smaller starting value form a sequence beginning with:

1, 2, 3, 6, 7, 9, 18, 25, 27, 54, 73, 97, … .

The record holder for total stopping time for numbers less than 100 million is 63,728,127, with 949 steps, for numbers less than 1 billion it is 670,617,279, with 986 steps, and for numbers less than 10 billion it is 9,780,657,630, with 1132 steps.,

The powers of two converge to one quickly because

is halved

times to reach one, and is never increased.

Program to calculate Hailstone sequences

A specific Hailstone sequence can be easily computed, as is shown by this pseudocode

Pseudocode

In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...

example:

function hailstone(n)

while n > 1

show n

if n is odd then

set n = 3n + 1

else

set n = n / 2

endif

endwhile

show n

This program halts when the sequence reaches 1, in order to avoid printing an endless cycle of 4, 2, 1. If the Collatz conjecture is true, the program will always halt (stop) no matter what positive starting integer is given to it.

m-cycles cannot occur

The proof of the conjecture can indirectly be done by proving the following:

no infinite divergent trajectory occurs
no cycle occurs

thus all numbers have a trajectory down to 1.

In 1977, R. Steiner, and in 2000 and 2002, J. Simons and B. de Weger (based on Steiner's work), proved the nonexistence of certain types of cycles.

Notation

To explain this we refer to the definition as given in the section Syracuse function below:

Define the transformation for odd positive integer numbers a and b, positive integer numbers A:

b = T(a;A) meaning b = (3a + 1)/2^A

where A has the maximum value which leaves b an integer.

Example:

a = 7. Then b = T(7, A) and 3a + 1 = 22,

so A = 1

b = (3×7 + 1)/2¹ = 11

11 = T(7;1)

Define the concatenation (extensible up to arbitrary length):

b = T(T(a;A);B) = T(a;A,B)

Example:

b = T(7; A, B) = T(7;1,1) = ((3×7 + 1)/2¹×3 + 1)/2^B = (3×11 + 1)/2^B = 34/2¹ = 17

17 = T(7;1,1)

Define a "one-peak-transformation" of L ascending and 1 descending exponents/steps:

b = T(a;1,1,1,1,1,....,1,A) = T(a;(1)_L,A)

with L (arbitrary) many exponents 1 and exactly one exponent A > 1

Example:

b = T(7;1,1,A) = T(7;(1)₂, A) = (17×3 + 1)/2^A = 52/2² = 13

13 = T(7;(1)₂,2)

then call the construction

a = T(a; (1)_L,A) // arbitrary positive value for number of increasing steps L

a "1-cycle" of length N = L + 1 (steps).

Theorems

Steiner proved in 1977 there is no 1-cycle. However many L steps may be chosen, a number x satisfying the loop-condition is never an integer.
Simons proved in 2000 (based on Steiner's method) there is no 2-cycle a = T(a;(1)_L,A,(1)_M,B) however many L and M steps may be chosen.
Simons/deWeger in 2003 extended their own proof up to "68-cycles": there is no m-cycle up to m = 68 a = T(a;(1)_L1,A₁,(1)_L2,A₂,...,(1)_L68,A₆₈). Whatever number of steps in L₁ to L₆₈ and whatever exponents A₁ to A₆₈ one may choose, there is no positive odd integer number a satisfying the cycle condition. Steiner claimed in a usenet discussion he could extend this up to m = 71.

Comment: These theorems were derived by results of the theory of rational approximation of transcendental numbers. Simons/deWeger concluded their article with the comment, that this method of approximation is exhausted with that results, and a completely different approach is needed to be able to proceed qualitatively.

Supporting arguments

Although the conjecture has not been proven, most mathematicians who have looked into the problem think the conjecture is true because experimental evidence and heuristic arguments support it.

Experimental evidence

The conjecture has been checked by computer for all starting values up to 20 × 2⁵⁸ ≈ 5.764. All initial values tested so far eventually end in the repeating cycle {4,2,1}, which has only three terms. It is also known that {4,2,1} is the only repeating cycle possible with fewer than 35400 terms.

Such computer evidence is not a proof that the conjecture is true. As shown in the cases of the Pólya conjecture

Pólya conjecture

In number theory, the Pólya conjecture stated that 'most' of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919, and proved false in 1958...

, the Mertens conjecture

Mertens conjecture

In mathematics, the Mertens conjecture is the incorrect statement that the Mertens function M is bounded by √n, which implies the Riemann hypothesis...

and the Skewes' number, sometimes a conjecture's only counterexamples are found when using very large numbers. Since sequentially examining all natural numbers is a process which can never be completed, such an approach can never demonstrate that the conjecture is true, merely that no counterexamples have yet been discovered.

A probabilistic heuristic

If one considers only the odd numbers in the sequence generated by the Collatz process, then each odd number is on average 3/4 of the previous one. (More precisely, the geometric mean of the ratios of outcomes is 3/4.) This yields a heuristic argument that every Hailstone sequence should decrease in the long run, although this is not evidence against other cycles, only against divergence. The argument is not a proof because it assumes that Hailstone sequences are assembled from uncorrelated probabilistic events. (It does rigorously establish that the 2-adic extension of the Collatz process has two division steps for every multiplication step for almost all 2-adic starting values.)

Rigorous bounds

Although it is not known rigorously whether all positive numbers eventually reach one according to the Collatz iteration, it is known that many numbers do so. In particular, Krasikov and Lagarias showed that the number of integers in the interval [1,x] that eventually reach one is at least proportional to x^0.84.

In reverse

There is another approach to prove the conjecture, which considers the bottom-up
method of growing the so called Collatz graph. The Collatz graph is a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

defined by the inverse relation

Relation (mathematics)

In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...

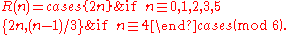
So, instead of proving that all natural numbers eventually lead to 1, we can prove that 1 leads to all natural numbers. For any integer n, n ≡ 1 (mod 2) iff

IFF

IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...

3n + 1 ≡ 4 (mod 6). Equivalently, (n − 1)/3 ≡ 1 (mod 2) iff n ≡ 4 (mod 6). Conjecturally, this inverse relation forms a tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

except for the 1–2–4 loop (the inverse of the 1–4–2 loop of the unaltered function f defined in the statement of the problem above). When the relation 3n + 1 of the function f is replaced by the common substitute "shortcut" relation (3n + 1)/2, the Collatz graph is defined by the inverse relation,

Conjecturally, this inverse relation forms a tree except for a 1–2 loop (the inverse of the 1–2 loop of the function f(n) revised as indicated above).

As an abstract machine that computes in base two

Repeated applications of the Collatz function can be represented as an abstract machine

Abstract machine

An abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...

that handles strings

String (computer science)

In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....

of bit

Bit

A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...

s. The machine will perform the following three steps on any odd number until only one "1" remains:

Append 1 to the (right) end of the number in binary (giving 2n + 1);
Add this to the original number by binary addition (giving 2n + 1 + n = 3n + 1);
Remove all trailing "0"s (i.e. repeatedly divide by two until the result is odd).

This prescription is plainly equivalent to computing a Hailstone sequence in base two.

Example

The starting number 7 is written in base two as 111. The resulting Hailstone sequence is:

As a parity sequence

For this section, consider the Collatz function in the slightly modified form

This can be done because when n is odd, 3n + 1 is always even.

If P(…) is the parity of a number, that is P(2n) = 0 and P(2n + 1) = 1, then we can define the Hailstone parity sequence for a number n as p_i = P(a_i), where a₀ = n, and a_i+1 = f(a_i).

Using this form for f(n), it can be shown that the parity sequences for two numbers m and n will agree in the first k terms if and only if m and n are equivalent modulo 2^k. This implies that every number is uniquely identified by its parity sequence, and moreover that if there are multiple Hailstone cycles, then their corresponding parity cycles must be different.

The proof is simple: it is easy to verify by hand that applying the f function k times to the number a·2^k + b will give the result a·3^c + d, where d is the result of applying the f function k times to b, and c is how many odd numbers were encountered during that sequence. So the parity of the first k numbers is determined purely by b, and the parity of the (k + 1)th number will change if the least significant bit of a is changed.

The Collatz Conjecture can be rephrased as stating that the Hailstone parity sequence for every number eventually enters the cycle 0 → 1 → 0.

As a tag system

For the Collatz function in the form

Hailstone sequences can be computed by the extremely simple

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.