Nowhere-zero flows
Encyclopedia
In graph theory
, nowhere-zero flows are a special type of network flow
which is related (by duality) to coloring
planar graphs. Let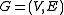
be a directed graph
and let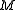
be an abelian group
. We say that a map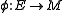
is a flow or an M-flow
if the following condition (sometimes called the Kirchoff Rule) is satisfied at every vertex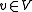
(here we let 
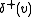denote the set of edges pointing away from 
and 
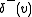the set of edges pointing toward 
).
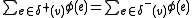
If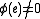
for every 
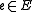, we call 
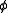a nowhere-zero flow. If 
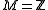and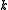 
is a positive integer with the property that 
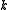for every edge 
, we say that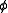 
is a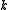 
-flow.
Consider a flow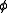
on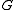 
and modify it by choosing an edge 
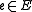, reversing it, and then replacing 
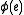with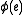 
. After this adjustment,
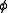is still a flow, and further this adjustment preserves the properties 
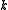-flow and nowhere-zero flow. Thus, the existence of a nowhere-zero 
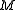-flow and the existence of a nowhere-zero 
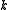-flow is independent of the orientation of the graph, and we will say that an (undirected) graph has a nowhere-zero 
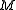-flow or k-flow if some (and thus every) orientation of it has such a flow.
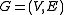be a directed bridgeless
graph drawn in the plane, and assume that the regions of this drawing are properly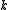
-colored with the colors {0, 1, 2, .., k − 1}. Now, construct a map 
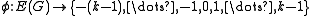by the following rule: if the edge 
has a region of color 
to the left and a region of color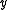 
to the right, then let 
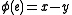. It is an easy exercise to show that 
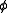is a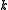 
-flow. Furthermore, since the regions were properly colored, 
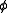is a nowhere-zero 
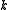-flow. It follows from this construction, that if 
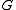and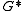 
are planar dual graphs and 
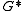is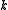 
-colorable, then 
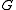has a nowhere-zero 
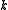-flow. Tutte proved that the converse of this statement is also true. Thus, for planar graphs, nowhere-zero flows are dual to colorings. Since nowhere-zero flows make sense for general graphs (not just graphs drawn in the plane), this study can be viewed as an extension of coloring theory for non-planar graphs.
edge has a proper coloring, no graph with a bridge
can have a nowhere-zero flow (in any group). It is easy to show that every graph without a bridge has a nowhere-zero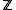
-flow (a form of Robbins theorem
), but interesting questions arise when we try to find nowhere-zero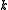
-flows for small values of 
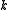. Two nice theorems in this direction are Jaeger's 4-flow theorem (every
4-edge-connected
graph has a nowhere-zero 4-flow) and Seymour's 6-flow theorem (every bridgeless graph has a nowhere-zero 6-flow).
W. T. Tutte
conjectured that every bridgeless graph has a nowhere-zero 5-flow and that every bridgeless graph that does not have the Petersen graph
as a minor
has a nowhere-zero 4-flow. For cubic graph
s with no Petersen minor, a 4-flow is known to exist as a consequence of the snark theorem
but for arbitrary graphs these conjectures remain open.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, nowhere-zero flows are a special type of network flow
Flow network
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
which is related (by duality) to coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
planar graphs. Let
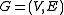be a directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
and let
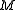be an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. We say that a map
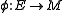is a flow or an M-flowCycle space
In graph theory, an area of mathematics, a cycle space is a vector space defined from an undirected graph; elements of the cycle space represent formal combinations of cycles in the graph....
if the following condition (sometimes called the Kirchoff Rule) is satisfied at every vertex
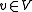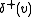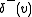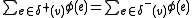
(here we let denote the set of edges pointing away from and the set of edges pointing toward ).If
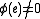for every 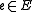, we call 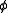a nowhere-zero flow. If 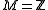and 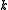is a positive integer with the property that 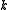for every edge , we say that 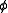is a 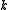-flow.Consider a flow
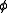on 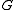and modify it by choosing an edge 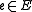, reversing it, and then replacing 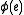with 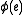. After this adjustment, 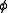is still a flow, and further this adjustment preserves the properties 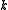-flow and nowhere-zero flow. Thus, the existence of a nowhere-zero 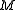-flow and the existence of a nowhere-zero 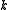-flow is independent of the orientation of the graph, and we will say that an (undirected) graph has a nowhere-zero 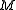-flow or k-flow if some (and thus every) orientation of it has such a flow.Flow/coloring duality
Let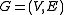 be a directed bridgelessBridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
graph drawn in the plane, and assume that the regions of this drawing are properly
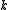-colored with the colors {0, 1, 2, .., k − 1}. Now, construct a map 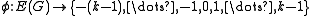by the following rule: if the edge has a region of color to the left and a region of color 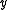to the right, then let 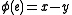. It is an easy exercise to show that 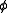is a 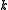-flow. Furthermore, since the regions were properly colored, 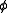is a nowhere-zero 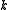-flow. It follows from this construction, that if 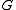and 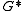are planar dual graphs and 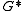is 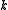-colorable, then 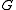has a nowhere-zero 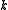-flow. Tutte proved that the converse of this statement is also true. Thus, for planar graphs, nowhere-zero flows are dual to colorings. Since nowhere-zero flows make sense for general graphs (not just graphs drawn in the plane), this study can be viewed as an extension of coloring theory for non-planar graphs.Theory
Just as no graph with a loopGlossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
edge has a proper coloring, no graph with a bridge
Glossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
can have a nowhere-zero flow (in any group). It is easy to show that every graph without a bridge has a nowhere-zero
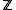-flow (a form of Robbins theoremRobbins theorem
In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs...
), but interesting questions arise when we try to find nowhere-zero
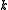-flows for small values of 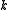. Two nice theorems in this direction are Jaeger's 4-flow theorem (every4-edge-connected
Glossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
graph has a nowhere-zero 4-flow) and Seymour's 6-flow theorem (every bridgeless graph has a nowhere-zero 6-flow).
W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
conjectured that every bridgeless graph has a nowhere-zero 5-flow and that every bridgeless graph that does not have the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
as a minor
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
has a nowhere-zero 4-flow. For cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s with no Petersen minor, a 4-flow is known to exist as a consequence of the snark theorem
Snark (graph theory)
In the mathematical field of graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a...
but for arbitrary graphs these conjectures remain open.