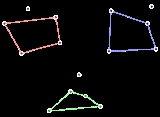
Happy Ending problem
Encyclopedia

Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
because it led to the marriage of George Szekeres
George Szekeres
George Szekeres AM was a Hungarian-Australian mathematician.-Early years:Szekeres was born in Budapest, Hungary as Szekeres György and received his degree in chemistry at the Technical University of Budapest. He worked six years in Budapest as an analytical chemist. He married Esther Klein in 1936...
and Esther Klein
Esther Szekeres
Esther Szekeres was a Hungarian-Australian mathematician. Esther Szekeres's Erdős number is 1.- Biography :...
) is the following statement:
- Theorem. Any set of five points in the plane in general positionGeneral positionIn algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
has a subset of four points that form the vertices of a convexConvex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
quadrilateralQuadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
.
This was one of the original results that led to the development of Ramsey theory
Ramsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
.
The Happy Ending theorem can be proven by a simple case analysis: If four or more points are vertices of the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
, any four such points can be chosen. If on the other hand the point set has the form of a triangle with two points inside it, the two inner points and one of the triangle sides can be chosen. See for an illustrated explanation of this proof, and for a more detailed survey of the problem than we provide here.
The Erdős–Szekeres conjecture states precisely a more general relationship between the number of points in a general-position point set and its largest convex polygon. It remains unproven, but less precise bounds are known.
Larger polygons

- Theorem. For any positive integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
N, any sufficiently large finite set of points in the plane in general position has a subset of N points that form the vertices of a convex polygon.
The proof appeared in the same paper that proves the Erdős–Szekeres theorem
Erdos–Szekeres theorem
In mathematics, the Erdős–Szekeres theorem is a finitary result that makes precise one of the corollaries of Ramsey's theorem. While Ramsey's theorem makes it easy to prove that every sequence of distinct real numbers contains either a monotonically increasing infinite subsequence, or a...
on monotonic subsequences in sequences of numbers.
Denoting by f(N) the minimal possible M for a set of M points in general position must contain a convex N-gon, it is known that
- f(3) = 3, trivially.
- f(4) = 5.
- f(5) = 9. A set of eight points with no convex pentagon is shown in the illustration, demonstrating that f(5) > 8; the more difficult part of the proof is to show that every set of nine points in general position contains the vertices of a convex pentagon.
- f(6) = 17.
- The value of f(N) is unknown for all N > 6; by the result of it is known to be finite.
On the basis of the known values of f(N) for N = 3, 4 and 5, Erdős and Szekeres conjectured in their original paper that
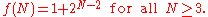
They proved later, by constructing explicit examples, that

but the best known upper bound when N ≥ 7 is

Empty polygons
One may also consider the question of whether any sufficiently large set of points in general position has an empty quadrilateral, pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
, etc.,
that is, one that contains no other input point. The original solution to the Happy Ending problem can be adapted to show that any five points in general position have an empty convex quadrilateral, as shown in the illustration, and any ten points in general position have an empty convex pentagon. However, there exist arbitrarily large sets of points in general position that contain no empty heptagon.
For a long time the question of the existence of empty hexagons remained open, but and proved that every sufficiently large point set in general position contains a convex empty hexagon. More specifically, Gerken showed that the number of points needed is no more than f(9) for the same function f defined above, while Nicolás showed that the number of points needed is no more than f(25). Valtr (2006) supplies a simplification of Gerken's proof that however requires more points, f(15) instead of f(9). At least 30 points are needed: there exists a set of 29 points in general position with no empty convex hexagon.
Related problems
The problem of finding sets of n points minimizing the number of convex quadrilaterals is equivalent to minimizing the crossing numberCrossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
in a straight-line drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
of a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. The number of quadrilaterals must be proportional to the fourth power of n, but the precise constant is not known.
It is straightforward to show that, in higher dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s, sufficiently large sets of points will have a subset of k points that forms the vertices of a convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
, for any k greater than the dimension: this follows immediately from existence of convex k-gons in sufficiently large planar point sets, by projecting the higher dimensional point set into an arbitrary two-dimensional subspace. However, the number of points necessary to find k points in convex position may be smaller in higher dimensions than it is in the plane, and it is possible to find subsets that are more highly constrained. In particular, in d dimensions, every d + 3 points in general position have a subset of d + 2 points that form the vertices of a cyclic polytope
Cyclic polytope
In mathematics, a cyclic polytope, denoted C, is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others...
. More generally, for every d and k > d there exists a number m(d,k) such that every set of m(d,k) points in general position has a subset of k points that form the vertices of a neighborly polytope
Neighborly polytope
In geometry and polyhedral combinatorics, a k-neighborly polytope is a convex polytope in which every set of k or fewer vertices forms a face. For instance, a 2-neighborly polytope is a polytope in which every pair of vertices is connected by an edge, forming a complete graph...
.
External links
- Happy ending problem and Ramsey-theoretic proof of the Erdős-Szekeres theorem on PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...

