
Cameron–Erdos conjecture
Encyclopedia
In combinatorics
, the Cameron–Erdős conjecture is the statement that the number of sum-free set
s contained in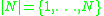 is
is 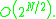
The sum of two odd numbers is even, so a set of odd numbers is always sum-free. There are odd numbers in |N|, and so
odd numbers in |N|, and so  subsets of odd numbers in |N|. The Cameron–Erdős conjecture says that this counts a constant proportion of the sum-free sets.
subsets of odd numbers in |N|. The Cameron–Erdős conjecture says that this counts a constant proportion of the sum-free sets.
The conjecture was stated by Peter Cameron
and Paul Erdős
in 1988. It was proved by Ben Green and independently by Alexander Sapozhenko in 2003.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the Cameron–Erdős conjecture is the statement that the number of sum-free set
Sum-free set
In additive combinatorics and number theory, a subset A of an abelian group G is said to be sum-free if the sumset A⊕A is disjoint from A...
s contained in
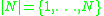 is
is 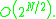
The sum of two odd numbers is even, so a set of odd numbers is always sum-free. There are
 odd numbers in |N|, and so
odd numbers in |N|, and so  subsets of odd numbers in |N|. The Cameron–Erdős conjecture says that this counts a constant proportion of the sum-free sets.
subsets of odd numbers in |N|. The Cameron–Erdős conjecture says that this counts a constant proportion of the sum-free sets.The conjecture was stated by Peter Cameron
Peter Cameron (mathematician)
Peter Jephson Cameron is an Australian mathematician who works ingroup theory, combinatorics, coding theory, and model theory. He is currently Professor of Mathematics at Queen Mary, University of London....
and Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
in 1988. It was proved by Ben Green and independently by Alexander Sapozhenko in 2003.

