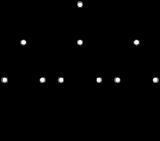
Moore graph
Encyclopedia
In graph theory
, a Moore graph is a regular graph
of degree
d and diameter k whose number of vertices equals the upper bound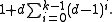
An equivalent definition of a Moore graph is that it is a graph of diameter k with girth 2k + 1. Moore graphs were named by after Edward F. Moore
, who posed the question of describing and classifying these graphs.
As well as having the maximum possible number of vertices for a given combination of degree and diameter,
Moore graphs have the minimum possible number of vertices for a regular graph with given degree and girth. That is, any Moore graph is a cage
. The formula for the number of vertices in a Moore graph can be generalized to allow a definition of Moore graphs with even girth as well as odd girth, and again these graphs are cages.
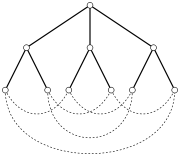 Let G be any graph with maximum degree d and diameter k, and consider the tree formed by breadth first search starting from any vertex v. This tree has 1 vertex at level 0 (v itself), and at most d vertices at level 1 (the neighbors of v). In the next level, there are at most d(d-1) vertices: each neighbor of v uses one of its adjacencies to connect to v and so can have at most d-1 neighbors at level 2. In general, a similar argument shows that at any level 1 ≤ i ≤ k, there can be at most d(d-1)i vertices. Thus, the total number of vertices can be at most
Let G be any graph with maximum degree d and diameter k, and consider the tree formed by breadth first search starting from any vertex v. This tree has 1 vertex at level 0 (v itself), and at most d vertices at level 1 (the neighbors of v). In the next level, there are at most d(d-1) vertices: each neighbor of v uses one of its adjacencies to connect to v and so can have at most d-1 neighbors at level 2. In general, a similar argument shows that at any level 1 ≤ i ≤ k, there can be at most d(d-1)i vertices. Thus, the total number of vertices can be at most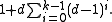
originally defined a Moore graph as a graph for which this bound on the number of vertices is met exactly. Therefore, any Moore graph has the maximum number of vertices possible among all graphs with maximum degree d and diameter k.
Later, showed that Moore graphs can equivalently be defined as having diameter k and girth 2k+1; these two requirements combine to force the graph to be d-regular for some d and to satisfy the vertex-counting formula.
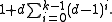
In a Moore graph, this bound on the number of vertices is met exactly. Each Moore graph has girth exactly 2k+1: it does not have enough vertices to have higher girth, and a shorter cycle would cause there to be too few vertices in the first k levels of some breadth first search tree.
Therefore, any Moore graph has the minimum number of vertices possible among all graphs with minimum degree d and diameter k: it is a cage
.
For even girth 2k, one can similarly form a breadth-first search tree starting from the midpoint of a single edge. The resulting bound on the minimum number of vertices in a graph of this girth with minimum degree d is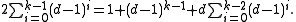
(The right hand side of the formula instead counts the number of vertices in a breadth first search tree starting from a single vertex, accounting for the possibility that a vertex in the last level of the tree may be adjacent to d vertices in the previous level.)
Thus, the Moore graphs are sometimes defined as including the graphs that exactly meet this bound. Again, any such graph must be a cage.
forms a Moore graph with degree 2, and any clique
forms a Moore graph with diameter 1. The other known Moore graphs are:
The Hoffman–Singleton theorem states that any Moore graph with girth 5 must have degree 2, 3, 7, or 57. The graphs with degree 2, 3, and 7 are the pentagon
, Petersen graph
, and Hoffman–Singleton graph, respectively. It is not known whether a Moore graph with girth 5 and degree 57 exists, but Higman
proved that it cannot be vertex-transitive
, unlike the known ones.
If the generalized definition of Moore graphs that allows even girth graphs is used, the Moore graphs also include the complete bipartite graph
Kn,n with girth four, the Heawood graph
with degree 3 and girth 6, and the Tutte–Coxeter graph with degree 3 and girth 8. More generally, it is known that, other than the graphs listed above, all Moore graphs must have girth 5, 6, 8, or 12.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a Moore graph is a regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
of degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
d and diameter k whose number of vertices equals the upper bound
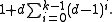
An equivalent definition of a Moore graph is that it is a graph of diameter k with girth 2k + 1. Moore graphs were named by after Edward F. Moore
Edward F. Moore
Edward Forrest Moore was an American professor of mathematics and computer science, the inventor of the Moore finite state machine, and an early pioneer of artificial life....
, who posed the question of describing and classifying these graphs.
As well as having the maximum possible number of vertices for a given combination of degree and diameter,
Moore graphs have the minimum possible number of vertices for a regular graph with given degree and girth. That is, any Moore graph is a cage
Cage (graph theory)
In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.Formally, an -graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. It is known that an -graph exists...
. The formula for the number of vertices in a Moore graph can be generalized to allow a definition of Moore graphs with even girth as well as odd girth, and again these graphs are cages.
Bounding vertices by degree and diameter

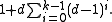
originally defined a Moore graph as a graph for which this bound on the number of vertices is met exactly. Therefore, any Moore graph has the maximum number of vertices possible among all graphs with maximum degree d and diameter k.
Later, showed that Moore graphs can equivalently be defined as having diameter k and girth 2k+1; these two requirements combine to force the graph to be d-regular for some d and to satisfy the vertex-counting formula.
Moore graphs as cages
Instead of upper bounding the number of vertices in a graph in terms of its maximum degree and its diameter, we can calculate via similar methods a lower bound on the number of vertices in terms of its minimum degree and its girth . Suppose G has minimum degree d and girth 2k+1. Choose arbitrarily a starting vertex v, and as before consider the breadth-first search tree rooted at v. This tree must have one vertex at level 0 (v itself), and at least d vertices at level 1. At level 2 (for k > 1), there must be at least d(d-1) vertices, because each vertex at level 1 has at least d-1 remaining adjacencies to fill, and no two vertices at level 1 can be adjacent to each other or to a shared vertex at level 2 because that would create a cycle shorter than the assumed girth. In general, a similar argument shows that at any level 1 ≤ i ≤ k, there must be at least d(d-1)i vertices. Thus, the total number of vertices must be at least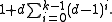
In a Moore graph, this bound on the number of vertices is met exactly. Each Moore graph has girth exactly 2k+1: it does not have enough vertices to have higher girth, and a shorter cycle would cause there to be too few vertices in the first k levels of some breadth first search tree.
Therefore, any Moore graph has the minimum number of vertices possible among all graphs with minimum degree d and diameter k: it is a cage
Cage (graph theory)
In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.Formally, an -graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. It is known that an -graph exists...
.
For even girth 2k, one can similarly form a breadth-first search tree starting from the midpoint of a single edge. The resulting bound on the minimum number of vertices in a graph of this girth with minimum degree d is
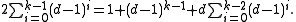
(The right hand side of the formula instead counts the number of vertices in a breadth first search tree starting from a single vertex, accounting for the possibility that a vertex in the last level of the tree may be adjacent to d vertices in the previous level.)
Thus, the Moore graphs are sometimes defined as including the graphs that exactly meet this bound. Again, any such graph must be a cage.
Examples
Any odd cycleCycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
forms a Moore graph with degree 2, and any clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
forms a Moore graph with diameter 1. The other known Moore graphs are:
- The Petersen graphPetersen graphIn the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
with degree 3, diameter 2, and girth 5.
- The Hoffman–Singleton graph with degree 7, diameter 2, and girth 5.
The Hoffman–Singleton theorem states that any Moore graph with girth 5 must have degree 2, 3, 7, or 57. The graphs with degree 2, 3, and 7 are the pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
, Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, and Hoffman–Singleton graph, respectively. It is not known whether a Moore graph with girth 5 and degree 57 exists, but Higman
Graham Higman
Graham Higman FRS was a leading British mathematician. He is known for his contributions to group theory....
proved that it cannot be vertex-transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
, unlike the known ones.
If the generalized definition of Moore graphs that allows even girth graphs is used, the Moore graphs also include the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Kn,n with girth four, the Heawood graph
Heawood graph
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
with degree 3 and girth 6, and the Tutte–Coxeter graph with degree 3 and girth 8. More generally, it is known that, other than the graphs listed above, all Moore graphs must have girth 5, 6, 8, or 12.
See also
- The Degree diameter problemDegree diameter problemIn graph theory, the degree diameter problem is the problem of finding the largest possible graph G of diameter k such that the largest degree of any of the vertices in G is at most d...
for graphs and digraphs - Table of degree diameter graphsTable of graphsIn graph theory, the degree diameter problem is the problem of finding the largest possible graph for a given maximum degree and diameter. The Moore bound sets limits on this, but for many years mathematicians in the field have been interested in a more precise answer...
External links
- BrouwerAndries BrouwerAndries Evert Brouwer is a Dutch mathematician and computer programmer, a professor at Eindhoven University of Technology . His varied research interests include several branches of discrete mathematics, particularly graph theory and coding theory...
and Haemers: Spectra of graphs

