Problems in Latin squares
Encyclopedia
In mathematics
, the theory of Latin squares is an active research area with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings. Problems posed here appeared in, for instance, the Loops (Prague) conferences and the Milehigh (Denver) conferences.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the theory of Latin squares is an active research area with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings. Problems posed here appeared in, for instance, the Loops (Prague) conferences and the Milehigh (Denver) conferences.
Bounds on maximal number of transversals in a Latin square
A transversal in a Latin squareLatin squareIn combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...
of order n is a set S of n cells such that every row and every column contains exactly one cell of S, and such that the symbols in S form {1,...,n}. Let T(n) be the maximum number of transversals in a Latin square of order n. Estimate T(n).
- Proposed: by Ian Wanless at Loops '03, Prague 2003
- Comments: Wanless, McKay and McLeod have bounds of the form cn < T(n) < dn n!, where c > 1 and d is about 0.6. A conjecture by Rivin, Vardi and Zimmermann (Rivin et al., 1994) says that you can place at least exp(c n log n) queensQueen (chess)The queen is the most powerful piece in the game of chess, able to move any number of squares vertically, horizontally, or diagonally. Each player starts the game with one queen, placed in the middle of the first rank next to the king. With the chessboard oriented correctly, the white queen starts...
in non-attacking positions on a toroidToroidToroid may refer to*Toroid , a doughnut-like solid whose surface is a torus.*Toroidal inductors and transformers which have wire windings on circular ring shaped magnetic cores.*Vortex ring, a toroidal flow in fluid mechanics....
al chessboardChessboardA chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...
(for some constant c). If true this would imply that T(n) > exp(c n log n). A related question is to estimate the number of transversals in the Cayley tableCayley tableA Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
s of cyclic groups of odd order. In other words, how many orthomorphisms do these groups have?
Characterization of Latin subsquares in multiplication tables of Moufang loops
Describe how all Latin subsquares in multiplication tables of Moufang loops arise.
- Proposed: by Aleš Drápal at Loops '03, Prague 2003
- Comments: It is well known that every Latin subsquare in a multiplication tableMultiplication tableIn mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
of a group G is of the form aH x Hb, where H is a subgroup of G and a, b are elements of G.
Densest partial Latin squares with Blackburn property
A partial Latin square has Blackburn property if whenever the cells (i,j) and (k,l) are occupied by the same symbol, the opposite corners (i,l) and (k,j) are empty. What is the highest achievable density of filled cells in a partial Latin square with the Blackburn property? In particular, is there some constant c > 0 such that we can always fill at least c n2 cells?
- Proposed: by Ian Wanless at Loops '03, Prague 2003
- Comments: In a paper to appear, Wanless has shown that if c exists then c < 0.463. He also constructed a family of partial Latin squares with the Blackburn property and asymptotic density of at least exp(-d(log n)1/2)) for constant d>0.
Largest power of 2 dividing the number of Latin squares
Letbe the number of Latin squares of order n. What is the largest integer
such that
divides
? Does
grow quadratically in n?
- Proposed: by Ian Wanless at Loops '03, Prague 2003
- Comments: Of course,
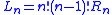where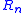 
is the number of reduced Latin squares of order n. This immediately gives a linear number of factors of 2. However, here are the prime factorizations of 
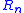for n=2, ... ,11:
2 3 4 5 6 7 8 9 10 11 1 1 22 237 26*3*72 210*3*5*1103 217*3*1361291 221*32*5231*3824477 228*32*5*31*37*547135293937 235*34*5*2801*2206499*62368028479
This table suggests that the power of 2 is growing superlinearly. The best current result is that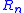
is always divisible by f!, where f is about n/2. See (McKay and Wanless, 2003). Two authors noticed the suspiciously high power of 2 (without being able to shed much light on it): (Alter, 1975), (Mullen, 1978).