Problems in loop theory and quasigroup theory

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, especially abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

, loop theory and quasigroup

Quasigroup

In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...

theory are active research areas with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings. Many of the problems posed here first appeared in the Loops (Prague) conferences and the Mile High (Denver) conferences.

Abelian by cyclic groups resulting in Moufang loops

Let L be a Moufang loop
Moufang loop
In mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...

with normal abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

(associative subloop) M of odd order such that L/M is a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

of order bigger than 3. (i) Is L a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

? (ii) If the orders of M and L/M are relatively prime, is L a group?

Proposed: by Michael Kinyon, based on (Chein and Rajah, 2000)

Comments: The assumption that L/M has order bigger than 3 is important, as there is a (commutative) Moufang loop L of order 81 with normal commutative subgroup of order 27.

(Doro's Conjecture) Does a Moufang loop with trivial nucleus necessarily have normal commutant?

Doro conjectured that a Moufang loop
Moufang loop
In mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...

with trivial nucleus has normal commutant. Is it true?

Proposed: at Milehigh conference on quasigroups, loops, and nonassocitaive systems, Denver 2005

Embedding CMLs of period 3 into alternative algebras

Conjecture: Any finite commutative Moufang loop
Moufang loop
In mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...

of period 3 can be embedded into a commutative alternative algebra
Alternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...

.

Proposed: by Alexander Grishkov at Loops '03, Prague 2003

Minimal presentations for loops M(G,2)

For a group , define on x by
, , , . Find a minimal presentation for the Moufang loop with respect to a presentation for .

Proposed: by Petr Vojtěchovský at Loops '03, Prague 2003

Comments: Chein showed in (Chein, 1974) that 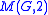is a Moufang loop that is nonassociative if and only if is nonabelian. Vojtěchovský (Vojtěchovský, 2003) found a minimal presentation for 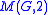when is a 2-generated group.

Moufang loops of order p²q³ and pq⁴

Let p and q be distinct odd primes. If q is not congruent to 1 modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

p, are all Moufang loops of order p²q³ groups? What about pq⁴?

Proposed: by Andrew Rajah at Loops '99, Prague 1999

Comments: The former has been solved by Rajah and Chee (2011) where they showed that for distinct odd primes p₁ < ··· < p_m < q < r₁ < ··· < r_n, all Moufang loops of order p₁²···p_m²q³r₁²···r_n² are groups if and only if q is not congruent to 1 modulo p_i for each i.

Moufang loops with non-normal commutant

Is there a Moufang loop whose commutant is not normal?

Proposed: by Andrew Rajah at Loops '03, Prague 2003

(Phillips' problem) Odd order Moufang loop with trivial nucleus

Is there a Moufang loop of odd order with trivial nucleus?

Proposed: by Andrew Rajah at Loops '03, Prague 2003

Presentations for finite simple Moufang loops

Find presentations for all nonassociative finite simple Moufang loops in the variety of Moufang loops.

Proposed: by Petr Vojtěchovský at Loops '03, Prague 2003

Comments: It is shown in (Vojtěchovský, 2003) that every nonassociative finite simple Moufang loop is generated by 3 elements, with explicit formulas for the generators.

Torsion in free Moufang loops

Let MF_n be the free
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....

Moufang loop with n generators.
Conjecture: MF₃ is torsion free but MF_n with n>4 is not.

Proposed: by Alexander Grishkov at Loops '03, Prague 2003

Nilpotency degree of the left multiplication group of a left Bol loop

For a left Bol loop Q, find some relation between the nilpotency
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...

degree of the left multiplication group of Q and the structure of Q.

Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005

Are two Bol loops with similar multiplication tables isomorphic?

Let , be two quasigroups defined on the same underlying set . The distance is the number of pairs in x such that ≠ . Call a class of finite quasigroups quadratic if there is a positive real number such that any two quasigroups , of order from the class satisfying < are isomorphic. Are Moufang loops quadratic? Are Bol loop
Bol loop
In mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....

s quadratic?

Proposed: by Aleš Drápal at Loops '99, Prague 1999

Comments: Drápal proved in (Drápal, 1992) that groups are quadratic with 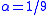, and in (Drápal, 2000) that 2-groups are quadratic with .

Campbell-Hausdorff series for analytic Bol loops

Determine the Campbell-Hausdorff series for analytic Bol loops.

Proposed: by M. A. Akivis and V. V. Goldberg at Loops '99, Prague 1999

Comments: The problem has been partially solved for local analytic Bruck loops in (Nagy, 2002).

Universally flexible loop that is not middle Bol

A loop is universally flexible if every one of its loop isotopes is flexible
Alternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...

, that is, satisfies (xy)x=x(yx). A loop is middle Bol if every one of its loop isotopes has the antiautomorphic inverse property, that is, satisfies (xy)^-1=y^-1x^-1. Is there a finite, universally flexible loop that is not middle Bol?

Proposed: by Michael Kinyon at Loops '03, Prague 2003

Finite simple Bol loop with nontrivial conjugacy classes

Is there a finite simple nonassociative Bol loop with nontrivial conjugacy classes?

Proposed: by Kenneth W. Johnson and Jonathan D. H. Smith at the 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009

Niemenmaa's conjecture and related problems

Let Q be a loop whose inner mapping group is nilpotent. Is Q nilpotent? Is Q solvable? If Q is also finite, is the multiplication group of Q solvable?

Proposed: at Loops '03 and '07, Prague 2003 and 2007

Comments: Niemenmaa conjectures that every loop with nilpotent inner mapping group is nilpotent.

Loops with abelian inner mapping group

Let Q be a loop with abelian inner mapping group. Is Q nilpotent? If so, is there a bound on the nilpotency class of Q? In particular, can the nilpotency class of Q be higher than 3?

Proposed: at Loops '07, Prague 2007

Comments: When the inner mapping group Inn(Q) is finite and abelian, then Q is nilpotent (Niemenaa and Kepka). The first question is therefore open only in the infinite case. Call loop Q of Csörgõ type if it is nilpotent of class at least 3, and Inn(Q) is abelian. No loop of Csörgõ type of nilpotency class higher than 3 is known. Loops of Csörgõ type exist (Csörgõ, 2004), Buchsteiner loops of Csörgõ type exist (Csörgõ, Drápal and Kinyon, 2007), and Moufang loops of Csörgõ type exist (Nagy and Vojtěchovský, 2007). On the other hand, there are no groups of Csörgõ type (folklore), there are no commutative Moufang loops of Csörgõ type (Bruck), and there are no Moufang p-loops of Csörgõ type for p>3 (Nagy and Vojtěchovský, 2007).

Number of nilpotent loops up to isomorphism

Determine the number of nilpotent loops of order 24 up to isomorphism.

Proposed: by Petr Vojtěchovský at the 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009

Comment: The counts are known for n<24, see (Daly and Vojtěchovský, 2010).

Classification of finite simple paramedial quasigroups

Classify the finite simple paramedial quasigroups.

Proposed: by Jaroslav Ježek and Tomáš Kepka at Loops '03, Prague 2003

Existence of infinite simple paramedial quasigroups

Are there infinite simple paramedial quasigroups?

Proposed: by Jaroslav Ježek and Tomáš Kepka at Loops '03, Prague 2003

Minimal isotopically universal varieties of quasigroups

A variety V of quasigroups is isotopically universal if every quasigroup is isotopic to a member of V. Is the variety of loops a minimal isotopically universal variety? Does every isotopically universal variety contain the variety of loops or its parastrophes?

Proposed: by Tomáš Kepka and Petr Němec at Loops '03, Prague 2003

Comments: Every quasigroup is isotopic to a loop, hence the variety of loops is isotopically universal.

Small quasigroups with quasigroup core

Does there exist a quasigroup Q of order q=14, 18, 26 or 42 such that the operation * defined on Q by x * y = y - xy is a quasigroup operation?

Proposed: by Parascovia Syrbu at Loops '03, Prague 2003

Comments: see (Conselo et al., 1998)

Parity of the number of quasigroups up to isomorphism

Let Q(n) be the number of isomorphism classes of quasigroups of order n. Is Q(n) odd for every n?

Proposed: by Douglas Stones at 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009

Comments: The numbers Q(n) are known for 0 < n < 11, and all these are odd.

Uniform construction of latin squares?

Construct a latin square L of order n as follows: Let G = K_n,n be the complete bipartite graph with distinct weights on its n² edges. Let M₁ be the cheapest matching in G, M₂ the cheapest matching in G with M₁ removed, and so on. Each matching M_i determines a permutation p_i of 1, ..., n. Let L be obtained from G by placing the permutation p_i into row i of L. Does this procedure result
in a uniform distribution on the space of latin squares of order n?

Proposed: by Gábor Nagy at the 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009

Bound on the size of multiplication groups

For a loop Q, let Mlt(Q) denote the multiplication group of Q, that is, the group generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

by all left and right translations. Is | Mlt( Q ) | < f( | Q | ) for some variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...

of loops and for some polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

f?

Proposed: at the Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005

Does every alternative loop have 2-sided inverses?

Does every alternative
Alternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...

loop, that is, every loop satisfying x(xy)=(xx)y and x(yy)=(xy)y, have 2-sided inverses?

Proposed: by Warren D. Smith

Comments: There are infinite alternative loops without 2-sided inverses, cf. (Ormes and Vojtěchovský, 2007)

Finite simple A-loop

Find a nonassociative finite simple A-loop, if such a loop exists.

Proposed: by Michael Kinyon at Loops '03, Prague 2003

Comments: It is known that if the order of such a loop is odd, the loop must have exponent p for some prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

p.

Universality of Osborn loops

A loop is Osborn if it satisfies the identity x((yz)x) = (x^λ\y)(zx). Is every Osborn loop universal, that is, is every isotope of an Osborn loop Osborn? If not, is there a nice identity characterizing universal Osborn loops?

Proposed: by Michael Kinyon at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005

Comments: Moufang and conjugacy closed loops are Osborn. See (Kinyon, 2005) for more.

Solved problems

The following problems were posed as open at various conferences and have since been solved.

Buchsteiner loop that is not conjugacy closed

Is there a Buchsteiner loop that is not conjugacy closed? Is there a finite simple Buchsteiner loop that is not conjugacy closed?

Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005

Solved by: Piroska Csörgõ, Aleš Drápal, and Michael Kinyon

Solution: The quotient of a Buchsteiner loop by its nucleus is an abelian group of exponent 4. In particular, no nonassociative Buchsteiner loop can be simple. There exists a Buchsteiner loop of order 128 which is not conjugacy closed.

Classification of Moufang loops of order 64

Classify nonassociative Moufang loops of order 64.

Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005

Solved by: Gábor P. Nagy and Petr Vojtěchovský

Solution: There are 4262 nonassociative Moufang loops of order 64. They were found by the method of group modifications in (Vojtěchovský, 2006), and it was shown in (Nagy and Vojtěchovský, 2007) that the list is complete. The latter paper uses a linear-algebraic
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

approach to Moufang loop extensions.

Conjugacy closed loop with nonisomorphic one-sided multiplication groups

Construct a conjugacy closed loop whose left multiplication group is not isomorphic to its right multiplication group.

Proposed: by Aleš Drápal at Loops '03, Prague 2003

Solved by: Aleš Drápal

Solution: There is such a loop of order 9. In can be obtained in the
LOOPS package by the command CCLoop(9,1).

Existence of a finite simple Bol loop

Is there a finite simple Bol loop
Bol loop
In mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....

that is not Moufang?

Proposed at: Loops '99, Prague 1999

Solved by: Gábor P. Nagy, 2007.

Solution: A simple Bol loop that is not Moufang will be called proper.
There are several families of proper simple Bol loops. A smallest proper simple Bol loop is of order 24.
There is also a proper simple Bol loop of exponent 2, and a proper simple Bol loop of odd order.
For details, see (Nagy 2007).
Comments: The above constructions solved additional two open problems:
- Is there a finite simple Bruck loop that is not Moufang? Yes, since any proper simple Bol loop of exponent 2 is Bruck.
- Is every Bol loop of odd order solvable? No, as witnessed by any proper simple Bol loop of odd order.

Left Bol loop with trivial right nucleus

Is there a finite non-Moufang left Bol loop
Bol loop
In mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....

with trivial right nucleus?

Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005

Solved by: Gábor P. Nagy, 2007

Solution: There is a finite simple left Bol loop of exponent 2 of order 96 with trivial right nucleus. Also, using an exact factorization of the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...

M₂₄, it is possible to construct a non-Moufang simple Bol loop which is a G-loop
Isotopy of loops
- Isotopy of quasigroups :Let and be quasigroups. A quasigroup homotopy from Q to P is a triple of maps from Q to P such that\alpha\circ\beta = \gamma\,for all x, y in Q...

.

Lagrange property for Moufang loops

Does every finite Moufang loop have the strong Lagrange property?

Proposed: by Orin Chein at Loops '99, Prague 1999

Solved by: Alexander Grishkov and Andrei Zavarnitsine, 2003

Solution: Every finite Moufang loop has the strong Lagrange property (SLP). Here is an outline of the proof:
- According to (Chein et al. 2003), it suffices to show SLP for nonassociative finite simple Moufang loops (NFSML).
- It thus suffices to show that the order of a maximal subloop of an NFSML L divides the order of L.
- A countable class of NFSMLs 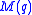was discovered in (Paige 1956), and no other NSFMLs exist by (Liebeck 1987).
- Grishkov and Zavarnitsine matched maximal subloops of loops 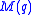with certain subgroups of groups with triality in (Grishkov and Zavarnitsine, 2003).

Quasivariety of cores of Bol loops

Is the class of cores of Bol loops a quasivariety?

Proposed: by Jonathan D. H. Smith and Alena Vanžurová at Loops '03, Prague 2003

Solved by: Alena Vanžurová, 2004.

Solution: No, the class of cores of Bol loops is not closed under subalgebras. Furthermore, the class of cores of groups is not closed under subalgebras. Here is an outline of the proof:
- Cores of abelian groups are medial
  Medial
  - Medial magmas :In abstract algebra, a medial magma is a set with a binary operation which satisfies the identity \cdot = \cdot , or more simply, xy\cdot uv = xu\cdot yv...
  
  , by (Romanowska and Smith, 1985), (Rozskowska-Lech, 1999).
- The smallest nonabelian group 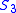has core containing a submagma
  Magma (algebra)
  In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
  
  of order 4 that is not medial.
- If is a core of a Bol loop, it is a core of a Bol loop of order 4, hence a core of an abelian group, a contradiction.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.