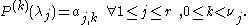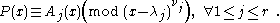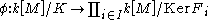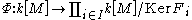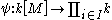Chinese remainder theorem
Encyclopedia
The Chinese remainder theorem is a result about congruences
in number theory
and its generalizations in abstract algebra
.
In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers. For example what is the single lowest number if repeatedly divided by 3 gives a remainder of 2; when divided by 5 gives a remainder of 3; and when divided by 7 gives a remainder of 2?
mathematician Sun Tzu
and later republished in a 1247 book by Qin Jiushao, the Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine Sections
) is a statement about simultaneous congruences (see modular arithmetic
).
Suppose n1, n2, …, nk are positive integer
s which are pairwise coprime
. Then, for any given sequence of integers a1,a2, …, ak, there exists an integer x solving the following system of simultaneous congruences.

Furthermore, all solutions x of this system are congruent modulo to the product N = n1n2…nk.
Hence for all
for all 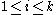 , if and only if
, if and only if 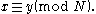
Sometimes, the simultaneous congruences can be solved even if the nis are not pairwise coprime. A solution x exists if and only if:
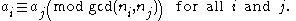
All solutions x are then congruent modulo the least common multiple
of the ni.
Sun Zi's work contains neither a proof nor a full algorithm. What amounts to an algorithm for solving this problem was described by Aryabhata
(6th century; see ). Special cases of the Chinese remainder theorem were also known to Brahmagupta
(7th century), and appear in Fibonacci
's Liber Abaci
(1202).
A modern restatement of the theorem in the algebraic language is that for a positive integer with prime factorization
with prime factorization 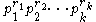 we have the isomorphism between a ring and the direct product of its prime power parts:
we have the isomorphism between a ring and the direct product of its prime power parts:
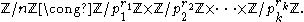
 . We will use the notation
. We will use the notation 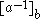 to denote the inverse of
to denote the inverse of 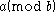 , it is defined exactly when
, it is defined exactly when  and
and 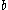 are coprime - the following construction explains why the coprimality condition is needed.
are coprime - the following construction explains why the coprimality condition is needed.
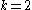 )
)
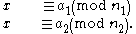
We define the value
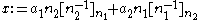
and it is seen to satisfy both congruences by reducing. For example
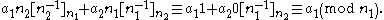
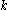 congruence equations. Let
congruence equations. Let 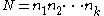 be the product of every modulus then define
be the product of every modulus then define
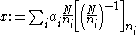
and this is seen to satisfy the system of congruences by a similar calculation as before.
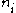 's are pairwise coprime
's are pairwise coprime
. (For simultaneous congruences when the moduli are not pairwise coprime, the method of successive substitution
can often yield solutions.)
Suppose, as above, that a solution is required for the system of congruences:
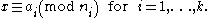
Again, to begin, the product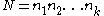 is defined. Then a solution x can be found as follows.
is defined. Then a solution x can be found as follows.
For each i the integers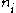 and
and 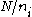 are coprime. Using the extended Euclidean algorithm
are coprime. Using the extended Euclidean algorithm
we can find integers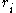 and
and 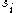 such that
such that 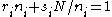 . Then, choosing the label
. Then, choosing the label 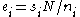 , the above expression becomes:
, the above expression becomes:
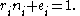
Consider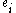 . The above equation guarantees that its remainder, when divided by
. The above equation guarantees that its remainder, when divided by 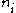 , must be 1. On the other hand, since it is formed as
, must be 1. On the other hand, since it is formed as 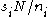 , the presence of N guarantees that it's evenly divisible by any
, the presence of N guarantees that it's evenly divisible by any 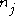 so long as
so long as 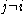 .
.
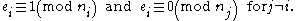
Because of this, combined with the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:
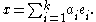
For example, consider the problem of finding an integer x such that

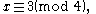

Using the extended Euclidean algorithm for x modulo 3 and 20 [4×5], we find (−13) × 3 + 2 × 20 = 1, i.e. e1 = 40. For x modulo 4 and 15 [3×5], we get (−11) × 4 + 3 × 15 = 1, i.e. e2 = 45. Finally, for x modulo 5 and 12 [3×4], we get 5 × 5 + (−2) × 12 = 1, i.e. e3 = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, [3 × 4 × 5 = 60] which means that they are all congruent to 11 modulo 60.
NOTE: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of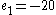 ,
, 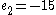 , and
, and 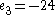 . These sets however will produce the same solution i.e. (-20)2+(-15)3+(-24)1=-109=11 modulo 60.
. These sets however will produce the same solution i.e. (-20)2+(-15)3+(-24)1=-109=11 modulo 60.
R the Chinese remainder theorem takes the following form: If u1, ..., uk are elements of R which are pairwise coprime
, and u denotes the product u1...uk, then the quotient ring
R/uR and the product ring
R/u1R× ... × R/ukR are isomorphic via the isomorphism
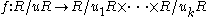
such that
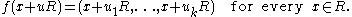
This map is well-defined and an isomorphism of rings; the inverse isomorphism can be constructed as follows. For each i, the elements ui and u/ui are coprime, and therefore there exist elements r and s in R with
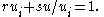
Set ei = s u/ui. Then the inverse of f is the map
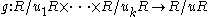
such that
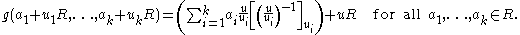
Note that this statement is a straightforward generalization of the above theorem about integer congruences: the ring Z of integer
s is a principal ideal domain, the surjectivity of the map f shows that every system of congruences of the form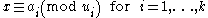
can be solved for x, and the injectivity of the map f shows that all the solutions x are congruent modulo u.
(meaning that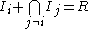 for all
for all 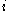 ),
),
then the product I of these ideals is equal to their intersection, and the quotient ring
R/I is isomorphic to the product ring
R/I1 x R/I2 x ... x R/Ik via the isomorphism
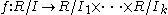
such that
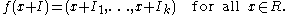
Here is a version of the theorem where R is not required to be commutative:
Let R be any ring with 1 (not necessarily commutative) and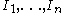 be pairwise coprime 2-sided ideals. Then the canonical R-module homomorphism
be pairwise coprime 2-sided ideals. Then the canonical R-module homomorphism 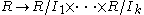 is onto, with kernel
is onto, with kernel 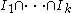 . Hence,
. Hence, 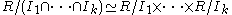 (as R-modules).
(as R-modules).
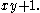 Then
Then 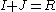 but
but 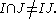
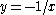 . Consider the polynomial
. Consider the polynomial 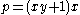 . Clearly
. Clearly 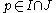 . Define a term in R as an element of the multiplicative monoid of R generated by x and y. Define the degree of a term as the usual degree of the term after the substitution
. Define a term in R as an element of the multiplicative monoid of R generated by x and y. Define the degree of a term as the usual degree of the term after the substitution 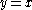 . On the other hand, suppose
. On the other hand, suppose 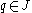 . Observe that a term in q of maximum degree depends on y otherwise q under the substitution
. Observe that a term in q of maximum degree depends on y otherwise q under the substitution 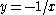 can not vanish. The same happens then for an element
can not vanish. The same happens then for an element 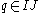 . Observe that the last y, from left to right, in a term of maximum degree in an element of
. Observe that the last y, from left to right, in a term of maximum degree in an element of 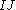 is preceded by more than one x. (We are counting here all the
is preceded by more than one x. (We are counting here all the
preceding xs. e.g. in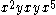 the last y is preceded by
the last y is preceded by 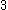 xs.) This proves that
xs.) This proves that 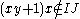 since that last y in a term of maximum degree (
since that last y in a term of maximum degree (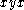 ) is preceded by only one x. Hence
) is preceded by only one x. Hence 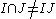 .
.
On the other hand, it is true in general that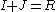 implies
implies 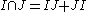 . To see this, note that
. To see this, note that 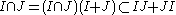 , while the opposite inclusion is obvious. Also, we have in general that, provided
, while the opposite inclusion is obvious. Also, we have in general that, provided 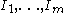 are
are
pairwise coprime two-sided ideals in R, the natural map
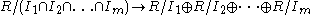
is an isomorphism. Note that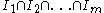 can be replaced by a sum over all orderings of
can be replaced by a sum over all orderings of
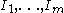 of their product (or just a sum over enough orderings, using inductively that
of their product (or just a sum over enough orderings, using inductively that 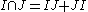
for coprime ideals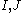 ).
).
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and its generalizations in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers. For example what is the single lowest number if repeatedly divided by 3 gives a remainder of 2; when divided by 5 gives a remainder of 3; and when divided by 7 gives a remainder of 2?
Theorem statement
The original form of the theorem, contained in a third-century AD book Sun Zi suanjing (孫子算經 The Mathematical Classic by Sun Zi) by ChineseChina
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
mathematician Sun Tzu
Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
and later republished in a 1247 book by Qin Jiushao, the Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine Sections
Mathematical Treatise in Nine Sections
The Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
) is a statement about simultaneous congruences (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
).
Suppose n1, n2, …, nk are positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s which are pairwise coprime
Pairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
. Then, for any given sequence of integers a1,a2, …, ak, there exists an integer x solving the following system of simultaneous congruences.

Furthermore, all solutions x of this system are congruent modulo to the product N = n1n2…nk.
Hence
 for all
for all 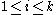 , if and only if
, if and only if 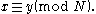
Sometimes, the simultaneous congruences can be solved even if the nis are not pairwise coprime. A solution x exists if and only if:
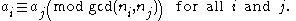
All solutions x are then congruent modulo the least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of the ni.
Sun Zi's work contains neither a proof nor a full algorithm. What amounts to an algorithm for solving this problem was described by Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
(6th century; see ). Special cases of the Chinese remainder theorem were also known to Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
(7th century), and appear in Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
's Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
(1202).
A modern restatement of the theorem in the algebraic language is that for a positive integer
 with prime factorization
with prime factorization 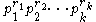 we have the isomorphism between a ring and the direct product of its prime power parts:
we have the isomorphism between a ring and the direct product of its prime power parts: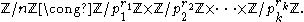
Existence
Existence can be seen by an explicit construction of . We will use the notation
. We will use the notation 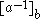 to denote the inverse of
to denote the inverse of 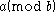 , it is defined exactly when
, it is defined exactly when  and
and 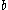 are coprime - the following construction explains why the coprimality condition is needed.
are coprime - the following construction explains why the coprimality condition is needed.Case of two equations
Given the system (corresponding to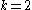 )
)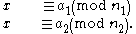
We define the value
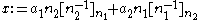
and it is seen to satisfy both congruences by reducing. For example
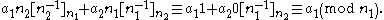
General case
The same type of construction works in the general case of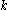 congruence equations. Let
congruence equations. Let 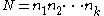 be the product of every modulus then define
be the product of every modulus then define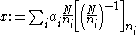
and this is seen to satisfy the system of congruences by a similar calculation as before.
A constructive algorithm to find the solution
The following algorithm only applies if the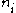 's are pairwise coprime
's are pairwise coprimePairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
. (For simultaneous congruences when the moduli are not pairwise coprime, the method of successive substitution
Method of successive substitution
In modular arithmetic, the method of successive substitution is a method of solving problems of simultaneous congruences by using the definition of the congruence equation...
can often yield solutions.)
Suppose, as above, that a solution is required for the system of congruences:
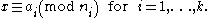
Again, to begin, the product
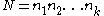 is defined. Then a solution x can be found as follows.
is defined. Then a solution x can be found as follows.For each i the integers
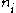 and
and 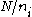 are coprime. Using the extended Euclidean algorithm
are coprime. Using the extended Euclidean algorithmExtended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
we can find integers
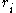 and
and 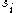 such that
such that 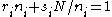 . Then, choosing the label
. Then, choosing the label 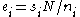 , the above expression becomes:
, the above expression becomes: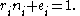
Consider
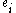 . The above equation guarantees that its remainder, when divided by
. The above equation guarantees that its remainder, when divided by 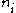 , must be 1. On the other hand, since it is formed as
, must be 1. On the other hand, since it is formed as 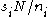 , the presence of N guarantees that it's evenly divisible by any
, the presence of N guarantees that it's evenly divisible by any 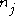 so long as
so long as 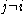 .
.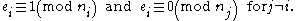
Because of this, combined with the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:
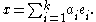
For example, consider the problem of finding an integer x such that

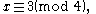

Using the extended Euclidean algorithm for x modulo 3 and 20 [4×5], we find (−13) × 3 + 2 × 20 = 1, i.e. e1 = 40. For x modulo 4 and 15 [3×5], we get (−11) × 4 + 3 × 15 = 1, i.e. e2 = 45. Finally, for x modulo 5 and 12 [3×4], we get 5 × 5 + (−2) × 12 = 1, i.e. e3 = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, [3 × 4 × 5 = 60] which means that they are all congruent to 11 modulo 60.
NOTE: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of
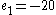 ,
, 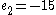 , and
, and 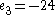 . These sets however will produce the same solution i.e. (-20)2+(-15)3+(-24)1=-109=11 modulo 60.
. These sets however will produce the same solution i.e. (-20)2+(-15)3+(-24)1=-109=11 modulo 60.Statement for principal ideal domains
For a principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
R the Chinese remainder theorem takes the following form: If u1, ..., uk are elements of R which are pairwise coprime
Pairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
, and u denotes the product u1...uk, then the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R/uR and the product ring
Product of rings
In mathematics, it is possible to combine several rings into one large product ring. This is done as follows: if I is some index set and Ri is a ring for every i in I, then the cartesian product Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e...
R/u1R× ... × R/ukR are isomorphic via the isomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
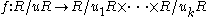
such that
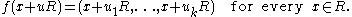
This map is well-defined and an isomorphism of rings; the inverse isomorphism can be constructed as follows. For each i, the elements ui and u/ui are coprime, and therefore there exist elements r and s in R with
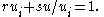
Set ei = s u/ui. Then the inverse of f is the map
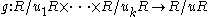
such that
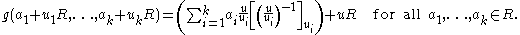
Note that this statement is a straightforward generalization of the above theorem about integer congruences: the ring Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is a principal ideal domain, the surjectivity of the map f shows that every system of congruences of the form
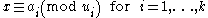
can be solved for x, and the injectivity of the map f shows that all the solutions x are congruent modulo u.
Statement for general rings
The general form of the Chinese remainder theorem, which implies all the statements given above, can be formulated for commutative rings and ideals. If R is a commutative ring and I1, ..., Ik are ideals of R which are pairwise coprime(meaning that
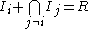 for all
for all 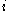 ),
),then the product I of these ideals is equal to their intersection, and the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R/I is isomorphic to the product ring
Product of rings
In mathematics, it is possible to combine several rings into one large product ring. This is done as follows: if I is some index set and Ri is a ring for every i in I, then the cartesian product Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e...
R/I1 x R/I2 x ... x R/Ik via the isomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
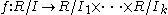
such that
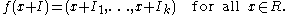
Here is a version of the theorem where R is not required to be commutative:
Let R be any ring with 1 (not necessarily commutative) and
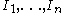 be pairwise coprime 2-sided ideals. Then the canonical R-module homomorphism
be pairwise coprime 2-sided ideals. Then the canonical R-module homomorphism 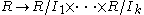 is onto, with kernel
is onto, with kernel 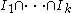 . Hence,
. Hence, 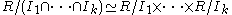 (as R-modules).
(as R-modules).Applications
- In the RSA algorithm calculations are made modulo n, where n is a product of two large prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p and q. 1024-, 2048- or 4096-bitBitA bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
integers n are commonly used, making calculations in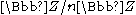 very time-consuming. By the Chinese remainder theorem, however, these calculations can be done in the isomorphic ring
very time-consuming. By the Chinese remainder theorem, however, these calculations can be done in the isomorphic ring 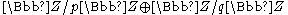 instead. Since p and q are normally of about the same size, that is about
instead. Since p and q are normally of about the same size, that is about 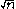 , calculations in the latter representation are much faster. Note that RSA algorithm implementations using this isomorphism are more susceptible to fault injectionFault injectionIn software testing, fault injection is a technique for improving the coverage of a test by introducing faults to test code paths, in particular error handling code paths, that might otherwise rarely be followed. It is often used with stress testing and is widely considered to be an important part...
, calculations in the latter representation are much faster. Note that RSA algorithm implementations using this isomorphism are more susceptible to fault injectionFault injectionIn software testing, fault injection is a technique for improving the coverage of a test by introducing faults to test code paths, in particular error handling code paths, that might otherwise rarely be followed. It is often used with stress testing and is widely considered to be an important part...
attacks.
- The Chinese remainder theorem may also be used to construct an elegant Gödel numbering for sequencesGödel numbering for sequencesA Gödel numbering for sequences provides us an effective way to represent each finite sequence of natural numbers as a single natural number. Of course, the embedding is surely possible set theoretically, but the emphasis is on the effectiveness of the functions manipulating such representations of...
, which is needed to prove Gödel's incompleteness theoremsGödel's incompleteness theoremsGödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
.
- The following example shows a connection with the classic polynomial interpolation theory. Let r complex points ("interpolation nodes")
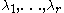 be given, together with the complex data
be given, together with the complex data 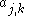 , for all
, for all 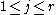 and
and 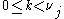 . The general Hermite interpolationHermite interpolationIn numerical analysis, Hermite interpolation, named after Charles Hermite, is a method of interpolating data points as a polynomial function. The generated Hermite polynomial is closely related to the Newton polynomial, in that both are derived from the calculation of divided differences.Unlike...
. The general Hermite interpolationHermite interpolationIn numerical analysis, Hermite interpolation, named after Charles Hermite, is a method of interpolating data points as a polynomial function. The generated Hermite polynomial is closely related to the Newton polynomial, in that both are derived from the calculation of divided differences.Unlike...
problem asks for a polynomial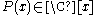 taking the prescribed derivatives in each node
taking the prescribed derivatives in each node 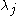 :
:
-
- Introducing the polynomials
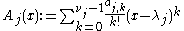 ,
,
- the problem may be equivalently reformulated as a system of
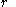 simultaneous congruences:
simultaneous congruences:
- By the Chinese remainder theorem in the principal ideal domain
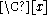 , there is a unique such polynomial
, there is a unique such polynomial 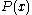 with degree
with degree 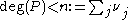 . A direct construction, in analogy with the above proof for the integer number case, can be performed as follows. Define the polynomials
. A direct construction, in analogy with the above proof for the integer number case, can be performed as follows. Define the polynomials 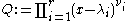 and
and 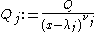 . The partial fraction decomposition of
. The partial fraction decomposition of 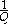 gives r polynomials
gives r polynomials 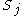 with degrees
with degrees 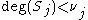 such that
such that
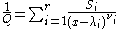 ,
,
- so that
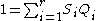 . Then a solution of the simultaneous congruence system is given by the polynomial
. Then a solution of the simultaneous congruence system is given by the polynomial
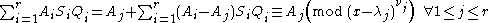 ;
;
- and the minimal degree solution is this one reduced modulo
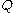 , that is the unique with degree less than n.
, that is the unique with degree less than n.
- The Chinese remainder theorem can also be used in Secret sharingSecret sharingSecret sharing refers to method for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together; individual shares are of no use on their own.More formally, in a...
, which consists of distributing a set of shares among a group of people who, all together (but no one alone), can recover a certain secret from the given set of shares. Each of the shares is represented in a congruence, and the solution of the system of congruences using the Chinese remainder theorem is the secret to be recovered. Secret Sharing using the Chinese Remainder Theorem uses, along with the Chinese remainder theorem, special sequences of integers that guarantee the impossibility of recovering the secret from a set of shares with less than a certain cardinality.
- The Good-Thomas fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithm exploits a re-indexing of the data based on the Chinese remainder theorem. See the Prime-factor FFT algorithmPrime-factor FFT algorithmThe prime-factor algorithm , also called the Good–Thomas algorithm , is a fast Fourier transform algorithm that re-expresses the discrete Fourier transform of a size N = N1N2 as a two-dimensional N1×N2 DFT, but only for the case where N1 and N2 are relatively prime...
article for details.
- Dedekind's theorem on the linear independence of characters states (in one of its most general forms) that if M is a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
and k is an integral domain, then any finite family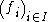 of distinct monoid homomorphisms
of distinct monoid homomorphisms 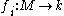 (where the monoid structure on k is given by multiplication) is linearly independent, i. e. every family
(where the monoid structure on k is given by multiplication) is linearly independent, i. e. every family 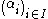 of elements
of elements 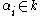 satisfying
satisfying 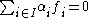 must be equal to the family
must be equal to the family 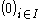 .
.
- Proof using the Chinese Remainder Theorem: First, assume that k is a field (otherwise, replace the integral domain k by its quotient field, and nothing will change). We can linearly extend the monoid homomorphisms
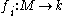 to k-algebra homomorphisms
to k-algebra homomorphisms 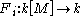 , where
, where 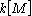 is the monoid ring of M over k. Then, the condition
is the monoid ring of M over k. Then, the condition 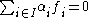 yields
yields 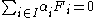 by linearity. Now, we notice that if
by linearity. Now, we notice that if 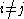 are two elements of the index set I, then the two k-linear maps
are two elements of the index set I, then the two k-linear maps 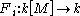 and
and 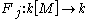 are not proportional to each other (because if they were, then
are not proportional to each other (because if they were, then 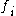 and
and 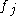 would also be proportional to each other, and thus equal to each other since
would also be proportional to each other, and thus equal to each other since 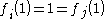 (since
(since 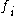 and
and 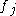 are monoid homomorphisms), contradicting the assumption that they be distinct). Hence, their kernels
are monoid homomorphisms), contradicting the assumption that they be distinct). Hence, their kernels 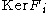 and
and 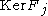 are distinct. Now,
are distinct. Now, 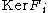 is a maximal ideal of
is a maximal ideal of 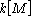 for every
for every 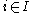 (since
(since 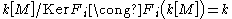 is a field), and the ideals
is a field), and the ideals 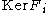 and
and 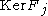 are coprime whenever
are coprime whenever 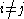 (since they are distinct and maximal). The Chinese Remainder Theorem (for general rings) thus yields that the map
(since they are distinct and maximal). The Chinese Remainder Theorem (for general rings) thus yields that the map
- given by
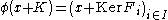 for all
for all 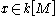
- is an isomorphism, where
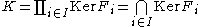 . Consequently, the map
. Consequently, the map
- given by
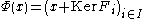 for all
for all 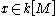
- is surjective. Under the isomorphisms
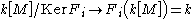 , this map
, this map 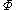 corresponds to the map
corresponds to the map
- given by
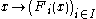 for every
for every 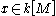 .
.
- Now,
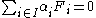 yields
yields 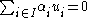 for every vector
for every vector 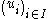 in the image of the map
in the image of the map 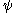 . Since
. Since 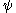 is surjective, this means that
is surjective, this means that 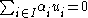 for every vector
for every vector 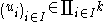 . Consequently,
. Consequently, 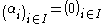 , qed.
, qed.
Non-commutative case: a counter-example
The Chinese remainder theorem does not hold in the non-commutative case. Consider the ring R of non-commutative real polynomials in x and y. Let I be the principal two-sided ideal generated by x and J the principal two-sided ideal generated by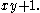 Then
Then 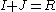 but
but 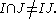
Proof
Observe that I is formed by all polynomials with an x in every term and that every polynomial in J vanishes under the substitution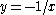 . Consider the polynomial
. Consider the polynomial 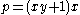 . Clearly
. Clearly 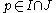 . Define a term in R as an element of the multiplicative monoid of R generated by x and y. Define the degree of a term as the usual degree of the term after the substitution
. Define a term in R as an element of the multiplicative monoid of R generated by x and y. Define the degree of a term as the usual degree of the term after the substitution 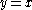 . On the other hand, suppose
. On the other hand, suppose 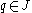 . Observe that a term in q of maximum degree depends on y otherwise q under the substitution
. Observe that a term in q of maximum degree depends on y otherwise q under the substitution 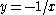 can not vanish. The same happens then for an element
can not vanish. The same happens then for an element 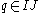 . Observe that the last y, from left to right, in a term of maximum degree in an element of
. Observe that the last y, from left to right, in a term of maximum degree in an element of 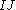 is preceded by more than one x. (We are counting here all the
is preceded by more than one x. (We are counting here all thepreceding xs. e.g. in
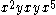 the last y is preceded by
the last y is preceded by 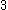 xs.) This proves that
xs.) This proves that 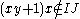 since that last y in a term of maximum degree (
since that last y in a term of maximum degree (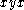 ) is preceded by only one x. Hence
) is preceded by only one x. Hence 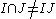 .
.On the other hand, it is true in general that
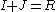 implies
implies 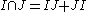 . To see this, note that
. To see this, note that 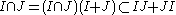 , while the opposite inclusion is obvious. Also, we have in general that, provided
, while the opposite inclusion is obvious. Also, we have in general that, provided 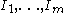 are
arepairwise coprime two-sided ideals in R, the natural map
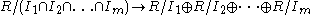
is an isomorphism. Note that
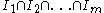 can be replaced by a sum over all orderings of
can be replaced by a sum over all orderings of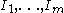 of their product (or just a sum over enough orderings, using inductively that
of their product (or just a sum over enough orderings, using inductively that 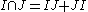
for coprime ideals
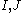 ).
).See also
- Covering system
- Hasse principleHasse principleIn mathematics, Helmut Hasse's local-global principle, also known as the Hasse principle, is the idea that one can find an integer solution to an equation by using the Chinese remainder theorem to piece together solutions modulo powers of each different prime number...
- Residue number systemResidue number systemA residue number system represents a large integer using a set of smaller integers, so that computation may be performed more efficiently...
- Secret sharing using the Chinese remainder theorem
External links
- "Chinese Remainder Theorem" by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
, 2007. - C# program and discussion at codeproject
- University of Hawaii System CRT by Lee Lady
- Full text of the Sunzi Suanjing (Chinese) - Chinese Text ProjectChinese Text ProjectThe Chinese Text Project is a digital library project that assembles collections of early Chinese texts. The name of the project in Chinese literally means "The Digitization Project of Chinese Philosophy Books", showing its focus on books related to Chinese philosophy...