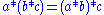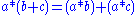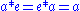Ring theory
Encyclopedia
In abstract algebra
, ring theory is the study of rings
—algebraic structure
s in which addition and multiplication are defined and have similar properties to those familiar from the integer
s. Ring theory studies the structure of rings, their representations
, or, in different language, modules, special classes of rings (group ring
s, division ring
s, universal enveloping algebra
s), as well as an array of properties that proved to be of interest both within the theory itself and for its applications, such as homological properties
and polynomial identities.
Commutative ring
s are much better understood than noncommutative ones. Algebraic geometry
and algebraic number theory
, which provide many natural examples of commutative rings, have driven much of the development of commutative ring theory. Because these two fields are so intimately connected with commutative rings, their theories are usually considered to be part of commutative algebra
and field theory
rather than of general ring theory.
Noncommutative ring
s are quite different in flavour, since more unusual behavior can arise. While the theory has developed in its own right, a fairly recent trend has sought to parallel the commutative development by building the theory of certain classes of noncommutative rings in a geometric fashion as if they were rings of function
s on (non-existent) 'noncommutative spaces'. This trend started in the 1980s with the development of noncommutative geometry
and with the discovery of quantum group
s. It has led to a better understanding of noncommutative rings, especially noncommutative Noetherian ring
s.
Please refer to the glossary of ring theory
for the definitions of terms used throughout ring theory.
algebraic geometry, and invariant theory. Central to the development of these subjects
were the rings of integers in algebraic number fields and algebraic function fields,
and the rings of polynomials in two or more variables.
Noncommutative ring theory began with attempts to extend the complex numbers
to various hypercomplex number
systems. The genesis of the theories of commutative
and noncommutative rings dates back to the early 19th century, while their
maturity was achieved only in the third decade of the 20th century.
More precisely, William Rowan Hamilton
put forth the quaternion
s and biquaternions; James Cockle presented tessarine
s and coquaternion
s; and William Kingdon Clifford
was an enthusiast of split-biquaternions, which he called algebraic motors. These non-commutative algebras, and the non-associative Lie algebra
s, were studied within universal algebra
before the subject was divided into particular mathematical structure
types. One sign of re-organization was the use of direct sums to describe algebraic structure.
The various hypercomplex numbers were identified with matrix ring
s by Joseph Wedderburn
(1908) and Emil Artin
(1928). Wedderburn's structure theorems were formulated for finite-dimensional algebras over a field
while Artin generalized them to Artinian ring
s.
(R, +), together with a second binary operation
* such that for all a, b and c in R,
also, if there exists a multiplicative identity in the ring, that is, an element e such that for all a in R,
then it is said to be a ring with unity. The number 1 is a common example of a unity.
The ring in which e is equal to the additive identity must have only one element. This ring is called the trivial ring.
Rings that sit inside other rings are called subring
s. Maps between rings which respect the ring operations are called ring homomorphism
s. Rings, together with ring homomorphisms, form a category
(the category of rings
). Closely related is the notion of ideals
, certain subsets of rings which arise as kernels
of homomorphisms and can serve to define factor rings. Basic facts about ideals, homomorphisms and factor rings are recorded in the isomorphism theorem
s and in the Chinese remainder theorem
.
A ring is called commutative if its multiplication is commutative. Commutative rings resemble familiar number systems, and various definitions for commutative rings are designed to recover properties known from the integer
s. Commutative rings are also important in algebraic geometry
. In commutative ring theory, numbers are often replaced by ideals
, and the definition of prime ideal
tries to capture the essence of prime number
s. Integral domains, non-trivial commutative rings where no two non-zero elements multiply to give zero, generalize another property of the integers and serve as the proper realm to study divisibility. Principal ideal domain
s are integral domains in which every ideal can be generated by a single element, another property shared by the integers. Euclidean domain
s are integral domains in which the Euclidean algorithm
can be carried out. Important examples of commutative rings can be constructed as rings of polynomial
s and their factor rings. Summary: Euclidean domain
=> principal ideal domain
=> unique factorization domain
=> integral domain => Commutative ring
.
Non-commutative rings resemble rings of matrices
in many respects. Following the model of algebraic geometry
, attempts have been made recently at defining non-commutative geometry based on non-commutative rings.
Non-commutative rings and associative algebra
s (rings that are also vector space
s) are often studied via their categories
of modules. A module
over a ring is an Abelian group
that the ring acts on as a ring of endomorphism
s, very much akin to the way field
s (integral domains in which every non-zero element is invertible) act on vector spaces. Examples of non-commutative rings are given by rings of square matrices
or more generally by rings of endomorphisms of Abelian groups or modules, and by monoid rings.
Structure theorems:
with a single object. It is therefore natural to consider arbitrary preadditive categories to be generalizations of rings. And indeed, many definitions and theorems originally given for rings can be translated to this more general context. Additive functors between preadditive categories generalize the concept of ring homomorphism, and ideals in additive categories can be defined as sets of morphism
s closed under addition and under composition with arbitrary morphisms.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, ring theory is the study of rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
—algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s in which addition and multiplication are defined and have similar properties to those familiar from the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Ring theory studies the structure of rings, their representations
Representation of an algebra
In abstract algebra, a representation of an associative algebra is a module for that algebra. Here an associative algebra is a ring...
, or, in different language, modules, special classes of rings (group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
s, division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s, universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
s), as well as an array of properties that proved to be of interest both within the theory itself and for its applications, such as homological properties
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and polynomial identities.
Commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s are much better understood than noncommutative ones. Algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, which provide many natural examples of commutative rings, have driven much of the development of commutative ring theory. Because these two fields are so intimately connected with commutative rings, their theories are usually considered to be part of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
rather than of general ring theory.
Noncommutative ring
Noncommutative ring
In mathematics, more specifically modern algebra and ring theory, a noncommutative ring is a ring whose multiplication is not commutative; that is, if R is a noncommutative ring, there exists a and b in R with a·b ≠ b·a, and conversely.Noncommutative rings are ubiquitous in mathematics, and occur...
s are quite different in flavour, since more unusual behavior can arise. While the theory has developed in its own right, a fairly recent trend has sought to parallel the commutative development by building the theory of certain classes of noncommutative rings in a geometric fashion as if they were rings of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s on (non-existent) 'noncommutative spaces'. This trend started in the 1980s with the development of noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
and with the discovery of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s. It has led to a better understanding of noncommutative rings, especially noncommutative Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s.
Please refer to the glossary of ring theory
Glossary of ring theory
Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.-Definition of a ring:...
for the definitions of terms used throughout ring theory.
History
Commutative ring theory originated in algebraic number theory,algebraic geometry, and invariant theory. Central to the development of these subjects
were the rings of integers in algebraic number fields and algebraic function fields,
and the rings of polynomials in two or more variables.
Noncommutative ring theory began with attempts to extend the complex numbers
to various hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
systems. The genesis of the theories of commutative
and noncommutative rings dates back to the early 19th century, while their
maturity was achieved only in the third decade of the 20th century.
More precisely, William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
put forth the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and biquaternions; James Cockle presented tessarine
Tessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s and coquaternion
Coquaternion
In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s; and William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
was an enthusiast of split-biquaternions, which he called algebraic motors. These non-commutative algebras, and the non-associative Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, were studied within universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
before the subject was divided into particular mathematical structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
types. One sign of re-organization was the use of direct sums to describe algebraic structure.
The various hypercomplex numbers were identified with matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
s by Joseph Wedderburn
Joseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
(1908) and Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
(1928). Wedderburn's structure theorems were formulated for finite-dimensional algebras over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
while Artin generalized them to Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
s.
Definition
Formally, a ring is an Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(R, +), together with a second binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
* such that for all a, b and c in R,
also, if there exists a multiplicative identity in the ring, that is, an element e such that for all a in R,
then it is said to be a ring with unity. The number 1 is a common example of a unity.
The ring in which e is equal to the additive identity must have only one element. This ring is called the trivial ring.
Rings that sit inside other rings are called subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s. Maps between rings which respect the ring operations are called ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s. Rings, together with ring homomorphisms, form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
(the category of rings
Category of rings
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
). Closely related is the notion of ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, certain subsets of rings which arise as kernels
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of homomorphisms and can serve to define factor rings. Basic facts about ideals, homomorphisms and factor rings are recorded in the isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
s and in the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
.
A ring is called commutative if its multiplication is commutative. Commutative rings resemble familiar number systems, and various definitions for commutative rings are designed to recover properties known from the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Commutative rings are also important in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. In commutative ring theory, numbers are often replaced by ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, and the definition of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
tries to capture the essence of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. Integral domains, non-trivial commutative rings where no two non-zero elements multiply to give zero, generalize another property of the integers and serve as the proper realm to study divisibility. Principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s are integral domains in which every ideal can be generated by a single element, another property shared by the integers. Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s are integral domains in which the Euclidean algorithm
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
can be carried out. Important examples of commutative rings can be constructed as rings of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s and their factor rings. Summary: Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
=> principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
=> unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
=> integral domain => Commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.
Non-commutative rings resemble rings of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in many respects. Following the model of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, attempts have been made recently at defining non-commutative geometry based on non-commutative rings.
Non-commutative rings and associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s (rings that are also vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s) are often studied via their categories
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of modules. A module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring is an Abelian group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that the ring acts on as a ring of endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s, very much akin to the way field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s (integral domains in which every non-zero element is invertible) act on vector spaces. Examples of non-commutative rings are given by rings of square matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
or more generally by rings of endomorphisms of Abelian groups or modules, and by monoid rings.
Some useful theorems
General:- Isomorphism theorems for rings
- Nakayama's lemma
Structure theorems:
- The Artin–Wedderburn theoremArtin–Wedderburn theoremIn abstract algebra, the Artin–Wedderburn theorem is a classification theorem for semisimple rings. The theorem states that an Artinian semisimple ring R is isomorphic to a product of finitely many ni-by-ni matrix rings over division rings Di, for some integers ni, both of which are uniquely...
determines the structure of semisimple rings. - The Jacobson density theoremJacobson density theoremIn mathematics, more specifically non-commutative ring theory, modern algebra, and module theory, the Jacobson density theorem is a theorem concerning simple modules over a ring R....
determines the structure of primitive ringPrimitive ringIn the branch of abstract algebra known as ring theory, a left primitive ring is a ring which has a faithful simple left module. Well known examples include endomorphism rings of vector spaces and Weyl algebras over fields of characteristic zero.- Definition :...
s. - Goldie's theoremGoldie's theoremIn mathematics, Goldie's theorem is a basic structural result in ring theory, proved by Alfred Goldie during the 1950s. What is now termed a right Goldie ring is a ring R that has finite uniform dimension as a right module over itself, and satisfies the ascending chain condition on right...
determines the structure of semiprime Goldie rings. - The Zariski-Samuel theorem determines the structure of a commutative principal ideal ringPrincipal ideal ringIn mathematics, a principal right ideal ring is a ring R in which every right ideal is of the form xR for some element x of R...
s. - The Hopkins–Levitzki theoremHopkins–Levitzki theoremIn the branch of abstract algebra called ring theory, the Akizuki-Hopkins–Levitzki theorem connects the descending chain condition and ascending chain condition in modules over semiprimary rings. A ring R is called semiprimary if R/J is semisimple and J is a nilpotent ideal, where J denotes the...
gives necessary and sufficient conditions for a Noetherian ringNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
to be an Artinian ringArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
. - Morita theory consists of theorems determining when two rings have "equivalent" module categories.
- Wedderburn's little theoremWedderburn's little theoremIn mathematics, Wedderburn's little theorem states that every finite domain is a field. In other words, for finite rings, there is no distinction between domains, skew-fields and fields.The Artin–Zorn theorem generalizes the theorem to alternative rings....
states that finite domainsDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
are fieldsField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Generalizations
Any ring can be seen as a preadditive categoryPreadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
with a single object. It is therefore natural to consider arbitrary preadditive categories to be generalizations of rings. And indeed, many definitions and theorems originally given for rings can be translated to this more general context. Additive functors between preadditive categories generalize the concept of ring homomorphism, and ideals in additive categories can be defined as sets of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s closed under addition and under composition with arbitrary morphisms.