
Continued fraction factorization
Encyclopedia
In number theory
, the continued fraction factorization method (CFRAC) is an integer factorization
algorithm
. It is a general-purpose algorithm, meaning that it is suitable for factoring any integer n, not depending on special form or properties. It was described by D. H. Lehmer
and R. E. Powers
in 1931, and developed as a computer algorithm by Michael A. Morrison and John Brillhart
in 1975.
The continued fraction method is based on Dixon's factorization method
. It uses convergents
in the regular continued fraction expansion
of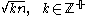 .
.
Since this is a quadratic irrational
, the continued fraction must be periodic (unless n is square, in which case the factorization is obvious).
It has a time complexity of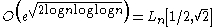 , in the O
, in the O
and L
notations.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the continued fraction factorization method (CFRAC) is an integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. It is a general-purpose algorithm, meaning that it is suitable for factoring any integer n, not depending on special form or properties. It was described by D. H. Lehmer
Derrick Henry Lehmer
Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...
and R. E. Powers
R. E. Powers
Details of the life of R.E. Powers are little-known; however, he was apparently the first mathematician to demonstrate that the Mersenne number M107 = 2107 − 1 was indeed prime. This was published in his article Certain composite Mersenne's numbers in 1916. Sometimes, mathematical textbooks...
in 1931, and developed as a computer algorithm by Michael A. Morrison and John Brillhart
John Brillhart
John David Brillhart is a mathematician, professor emeritus at the University of Arizona. He is known for his work in integer factorization, including the development of the continued fraction factorization method. He has been a principal participant in the Cunningham project.Brillhart received his...
in 1975.
The continued fraction method is based on Dixon's factorization method
Dixon's factorization method
In number theory, Dixon's factorization method is a general-purpose integer factorization algorithm; it is the prototypical factor base method, and the only factor base method for which a run-time bound not reliant on conjectures about the smoothness properties of values of a polynomial is...
. It uses convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
in the regular continued fraction expansion
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
of
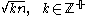 .
.Since this is a quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
, the continued fraction must be periodic (unless n is square, in which case the factorization is obvious).
It has a time complexity of
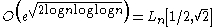 , in the O
, in the OBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
and L
L-notation
L-notation is an asymptotic notation analogous to big-O notation, denoted as L_n[\alpha,c] for a bound variable n tending to infinity. Like big-O notation, it is usually used to roughly convey the computational complexity of a particular algorithm....
notations.

