.gif)
Tangle (mathematics)
Encyclopedia
In mathematics
, a tangle can mean one of two related concepts:
The balance of this article discusses Conway's sense of tangles; for the link theory sense, see that article.
Two n-tangles are considered equivalent if there is an ambient isotopy of one tangle to the other keeping the boundary of the 3-ball fixed. Tangle theory can be considered analogous to knot theory
except instead of closed loops we use strings whose ends are nailed down. See also braid theory
.
with respect to the projection onto the flat disc bounded by the great circle. The projection then gives us a tangle diagram, where we make note of over and undercrossings as with knot diagrams.
Tangles often show up as tangle diagrams in knot or link diagrams and can be used as building blocks for link diagrams, e.g. pretzel link
s.
A rational tangle is a 2-tangle that is homeomorphic to the trivial 2-tangle as a map of pairs consisting of the 3-ball and two arcs. The four endpoints of the arcs on the boundary circle of a tangle diagram are usually referred as NE, NW, SW, SE, with the symbols referring to the compass directions.
An arbitrary tangle diagram of a rational tangle may look very complicated, but there is always a diagram of a particular simple form: start with a tangle diagram consisting of two horizontal (vertical) arcs; add a "twist", i.e. a single crossing by switching the NE and SE endpoints (SW and SE endpoints); continue by adding more twists using either the NE and SE endpoints or the SW and SE endpoints. One can suppose each twist does not change the diagram inside a disc containing previously created crossings.
We can describe such a diagram by considering the numbers given by consecutive twists around the same set of endpoints, e.g. (2, 1, -3) means start with two horizontal arcs, then 2 twists using NE/SE endpoints, then 1 twist using SW/SE endpoints, and then 3 twists using NE/SE endpoints but twisting in the opposite direction from before. The list begins with 0 if you start with two vertical arcs. The diagram with two horizontal arcs is then (0), but we assign (0, 0) to the diagram with vertical arcs. A convention is needed to describe a "positive" or "negative" twist. Often, "rational tangle" refers to a list of numbers representing a simple diagram as described.
The fraction of a rational tangle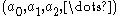
is then defined as the number given by the continued fraction 
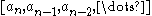. The fraction given by (0,0) is defined as 
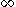. Conway proved that the fraction is well-defined and completely determines the rational tangle up to tangle equivalence (Conway 1970). An accessible proof of this fact is given in (Kauffman and Lambropoulou 2004). Conway also defined a fraction of an arbitrary tangle by using the Alexander polynomial
.
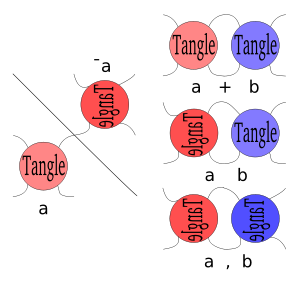
There is an "arithmetic" of tangles with addition, multiplication, and reciprocal operations. An algebraic tangle is obtained from the addition and multiplication of rational tangles.
The numerator closure of a rational tangle is defined as the link obtained by joining the "north" endpoints together and the "south" endpoints also together. The denominator closure is defined similarly by grouping the "east" and "west" endpoints. Rational links are defined to be such closures of rational tangles.
can be analysed with the help of tangle theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a tangle can mean one of two related concepts:
- In John Conway'sJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
definition, an n-tangle is a proper embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of the disjoint union of n arcs into a 3-ballBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
; the embedding must send the endpoints of the arcs to 2n marked points on the ball's boundary. - In link theoryLink (knot theory)In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
, a tangle is an embedding of n arcs and m circles into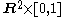
– the difference from the previous definition is that it includes circles as well as arches, and partitions the boundary into two (isomorphic) pieces, which is algebraically more convenient – it allows one to add tangles by stacking them, for instance.
The balance of this article discusses Conway's sense of tangles; for the link theory sense, see that article.
Two n-tangles are considered equivalent if there is an ambient isotopy of one tangle to the other keeping the boundary of the 3-ball fixed. Tangle theory can be considered analogous to knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
except instead of closed loops we use strings whose ends are nailed down. See also braid theory
Braid theory
In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...
.
Tangle diagrams
Without loss of generality, consider the marked points on the 3-ball boundary to lie on a great circle. The tangle can be arranged to be in general positionGeneral position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
with respect to the projection onto the flat disc bounded by the great circle. The projection then gives us a tangle diagram, where we make note of over and undercrossings as with knot diagrams.
Tangles often show up as tangle diagrams in knot or link diagrams and can be used as building blocks for link diagrams, e.g. pretzel link
Pretzel link
In knot theory, a branch of mathematics, a pretzel link is a special kind of link. A pretzel link which is also a knot is a pretzel knot....
s.
Rational and algebraic tangles
An arbitrary tangle diagram of a rational tangle may look very complicated, but there is always a diagram of a particular simple form: start with a tangle diagram consisting of two horizontal (vertical) arcs; add a "twist", i.e. a single crossing by switching the NE and SE endpoints (SW and SE endpoints); continue by adding more twists using either the NE and SE endpoints or the SW and SE endpoints. One can suppose each twist does not change the diagram inside a disc containing previously created crossings.
We can describe such a diagram by considering the numbers given by consecutive twists around the same set of endpoints, e.g. (2, 1, -3) means start with two horizontal arcs, then 2 twists using NE/SE endpoints, then 1 twist using SW/SE endpoints, and then 3 twists using NE/SE endpoints but twisting in the opposite direction from before. The list begins with 0 if you start with two vertical arcs. The diagram with two horizontal arcs is then (0), but we assign (0, 0) to the diagram with vertical arcs. A convention is needed to describe a "positive" or "negative" twist. Often, "rational tangle" refers to a list of numbers representing a simple diagram as described.
The fraction of a rational tangle
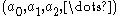is then defined as the number given by the continued fraction 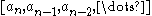. The fraction given by (0,0) is defined as 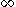. Conway proved that the fraction is well-defined and completely determines the rational tangle up to tangle equivalence (Conway 1970). An accessible proof of this fact is given in (Kauffman and Lambropoulou 2004). Conway also defined a fraction of an arbitrary tangle by using the Alexander polynomialAlexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
.
There is an "arithmetic" of tangles with addition, multiplication, and reciprocal operations. An algebraic tangle is obtained from the addition and multiplication of rational tangles.
The numerator closure of a rational tangle is defined as the link obtained by joining the "north" endpoints together and the "south" endpoints also together. The denominator closure is defined similarly by grouping the "east" and "west" endpoints. Rational links are defined to be such closures of rational tangles.
Conway notation
One motivation for Conway's study of tangles was to provide a notation for knots more systematic than the traditional enumeration found in tables.Applications
Tangles have been shown to be useful in studying DNA topology. The action of a given enzymeEnzyme
Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...
can be analysed with the help of tangle theory.
External links
- David MacKay: Metapost code for drawing tangles.
- Rational Tangles