
Convergent (continued fraction)
Encyclopedia
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction
The nth convergent is also known as the nth approximant of a continued fraction.
. Each convergent of that continued fraction is in a sense the best possible rational approximation to that real number, for a given number of digits. Such a convergent is usually about as accurate as a finite decimal expansion having as many digits as the total number of digits in the nth numerator and nth denominator. For example, the third convergent 333/106 for π (Pi) is roughly 3.1415094, which is not quite as accurate as the 6-digit 3.14159; the fourth convergent 355/113 = 3.14159292 is more accurate than the 6-digit decimal.
By the determinant formula it appears that the successive convergents Ak/Bk of a regular continued fraction are connected by the formula
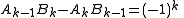
This implies, in particular, that the greatest common divisor
(Ak, Bk) = 1; in other words, each convergent of a regular continued fraction, as given by the fundamental recurrence formulas
, is automatically expressed in lowest terms.
More detailed properties of best rational approximations and convergents of π are discussed in the continued fraction
article.
a continued fraction is usually written as
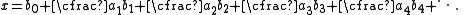
where the ai and the bi are integer
s. The ai are the partial numerators of the continued fraction x. The bi are the partial denominators, and the ratios ai / bi are the partial quotients. The convergents of this fraction can be computed by using the fundamental recurrence formulas
.
An infinite continued fraction converges
if the sequence
of convergents approaches a limit. If the sequence of convergents does not approach a limit, the continued fraction is divergent.
Because of the way the partial denominators and partial numerators interact with each other as the successive convergents are calculated, the convergence problem for continued fractions is inherently more difficult than it is for infinite series. The Śleszyński–Pringsheim theorem
provides one sufficient condition for convergence.
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
The nth convergent is also known as the nth approximant of a continued fraction.
Representation of real numbers
Every real number can be expressed as a regular continued fraction in canonical formContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
. Each convergent of that continued fraction is in a sense the best possible rational approximation to that real number, for a given number of digits. Such a convergent is usually about as accurate as a finite decimal expansion having as many digits as the total number of digits in the nth numerator and nth denominator. For example, the third convergent 333/106 for π (Pi) is roughly 3.1415094, which is not quite as accurate as the 6-digit 3.14159; the fourth convergent 355/113 = 3.14159292 is more accurate than the 6-digit decimal.
By the determinant formula it appears that the successive convergents Ak/Bk of a regular continued fraction are connected by the formula
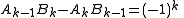
This implies, in particular, that the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(Ak, Bk) = 1; in other words, each convergent of a regular continued fraction, as given by the fundamental recurrence formulas
Fundamental recurrence formulas
In the theory of continued fractions, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents...
, is automatically expressed in lowest terms.
More detailed properties of best rational approximations and convergents of π are discussed in the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
article.
Convergents and convergence
In mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
a continued fraction is usually written as
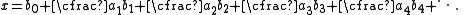
where the ai and the bi are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. The ai are the partial numerators of the continued fraction x. The bi are the partial denominators, and the ratios ai / bi are the partial quotients. The convergents of this fraction can be computed by using the fundamental recurrence formulas
Fundamental recurrence formulas
In the theory of continued fractions, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents...
.
An infinite continued fraction converges
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
if the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of convergents approaches a limit. If the sequence of convergents does not approach a limit, the continued fraction is divergent.
Because of the way the partial denominators and partial numerators interact with each other as the successive convergents are calculated, the convergence problem for continued fractions is inherently more difficult than it is for infinite series. The Śleszyński–Pringsheim theorem
Śleszyński–Pringsheim theorem
In mathematics, the Śleszyński–Pringsheim theorem is a statement about convergence of certain continued fractions. It was discovered by Ivan Śleszyński and Alfred Pringsheim in the late 19th century....
provides one sufficient condition for convergence.

