
Tychonoff space
Encyclopedia
In topology
and related branches of mathematics
, Tychonoff spaces and completely regular spaces are kinds of topological space
s.
These conditions are examples of separation axiom
s.
Tychonoff spaces are named after Andrey Nikolayevich Tychonoff
, whose Russian
name (Тихонов) is variously rendered as "Tychonov", "Tikhonov", "Tihonov", "Tichonov" etc.
X is a completely regular space if given any closed set
F and any point
x that does not belong to F, there is
a continuous function f from X to the real line
R such that f(x) is and f(y) is for every y in F.
In other terms, this condition says that x and F can be separated by a continuous function
.
X is a Tychonoff space, or T3½ space, or Tπ space, or completely T3 space if it is both completely regular and Hausdorff
.
Note that some mathematical literature uses different definitions for the term "completely regular" and the terms involving "T".
The definitions that we have given here are the ones usually used today; however, some authors switch the meanings of the two kinds of terms, or use all terms synonymously for only one condition.
In Wikipedia, we will use the terms "completely regular" and "Tychonoff" freely, but we'll avoid the less clear "T" terms.
In other literature, you should take care to find out which definitions the author is using.
(The phrase "completely regular Hausdorff", however, is unambiguous, and always means a Tychonoff space.)
For more on this issue, see History of the separation axioms
.
Completely regular spaces and Tychonoff spaces are related through the notion of Kolmogorov equivalence.
A topological space is Tychonoff if and only if it's both completely regular and T0
.
On the other hand, a space is completely regular if and only if its Kolmogorov quotient is Tychonoff.
is Tychonoff, or at least completely regular.
For example, the real line
is Tychonoff under the standard Euclidean topology
.
Other examples include:
. Specifically, complete regularity is preserved by taking arbitrary initial topologies and the Tychonoff property is preserved by taking point-separating initial topologies. It follows that:
Like all separation axioms, completely regularity is not preserved by taking final topologies
. In particular, quotients
of completely regular spaces need not be regular
. Quotients of Tychonoff spaces need not even be Hausdorff
. There are closed quotients of the Moore plane
which provide counterexamples.
real-valued continuous functions.
Completely regular spaces can be characterized by the fact that their topology is completely determined by C(X) or C*(X). In particular:
Given an arbitrary topological space (X, τ) there is a universal way of associating a completely regular space with (X, τ). Let ρ be the initial topology on X induced by Cτ(X) or, equivalently, the topology generated by the basis of cozero sets in (X, τ). Then ρ will be the finest completely regular topology on X which is coarser than τ. This construction is universal
in the sense that any continuous function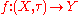
to a completely regular space Y will be continuous on (X, ρ). In the language of category theory
, the functor
which sends (X, τ) to (X, ρ) is left adjoint to the inclusion functor CReg → Top. Thus the category of completely regular spaces CReg is a reflective subcategory
of Top, the category of topological spaces
. By taking Kolmogorov quotients, one sees that the subcategory of Tychonoff spaces is also reflective.
One can show that Cτ(X) = Cρ(X) in the above construction so that the rings C(X) and C*(X) are typically only studied for completely regular spaces X.
The category of real compact
Tychonoff spaces is anti-equivalent to the category of the rings C(X) (where X is real compact) together with ring homomorphisms as maps. For example one can reconstruct $X$ from C(X) when X is (real) compact. The algebraic theory of these rings is therefore subject of intensive studies.
A vast generalisation of this class of rings which still resembles many properties of Tychonoff spaces but is also applicable in real algebraic geometry
, is the class of real closed ring
s.
embedded
in compact Hausdorff spaces. More precisely, for every Tychonoff space X, there exists a compact Hausdorff space K such that X is homeomorphic to a subspace of K.
In fact, one can always choose K to be a cube
(i.e. a possibly infinite product of unit interval
s). Every cube is compact Hausdorff as a consequence of Tychonoff's theorem
. Since every subspace of a compact Hausdorff space is Tychonoff one has:
s of X. Given any embedding of a Tychonoff space X in a compact Hausdorff space K the closure
of the image of X in K is a compactification of X.
Among those Hausdorff compactifications, there is a unique "most general" one, the Stone–Čech compactification
βX.
It is characterised by the universal property
that, given a continuous map f from X to any other compact Hausdorff space Y, there is a unique continuous map g from βX to Y that extends f in the sense that f is the composition of g and j.
has a completely regular topology and every completely regular space X is uniformizable. A topological space admits a separated uniform structure if and only if it is Tychonoff.
Given a completely regular space X there is usually more than one uniformity on X that is compatible with the topology of X. However, there will always be a finest compatible uniformity, called the fine uniformity on X. If X is Tychonoff, then the uniform structure can be chosen so that βX becomes the completion of the uniform space X.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Tychonoff spaces and completely regular spaces are kinds of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s.
These conditions are examples of separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s.
Tychonoff spaces are named after Andrey Nikolayevich Tychonoff
Andrey Nikolayevich Tychonoff
Andrey Nikolayevich Tikhonov was a Soviet and Russian mathematician known for important contributions to topology, functional analysis, mathematical physics, and ill-posed problems. He was also inventor of magnetotellurics method in geology. Tikhonov originally published in German, whence the...
, whose Russian
Russian language
Russian is a Slavic language used primarily in Russia, Belarus, Uzbekistan, Kazakhstan, Tajikistan and Kyrgyzstan. It is an unofficial but widely spoken language in Ukraine, Moldova, Latvia, Turkmenistan and Estonia and, to a lesser extent, the other countries that were once constituent republics...
name (Тихонов) is variously rendered as "Tychonov", "Tikhonov", "Tihonov", "Tichonov" etc.
Definitions
Suppose that X is a topological space.X is a completely regular space if given any closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
F and any point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
x that does not belong to F, there is
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a continuous function f from X to the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R such that f(x) is and f(y) is for every y in F.
In other terms, this condition says that x and F can be separated by a continuous function
Separated sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
.
X is a Tychonoff space, or T3½ space, or Tπ space, or completely T3 space if it is both completely regular and Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
Note that some mathematical literature uses different definitions for the term "completely regular" and the terms involving "T".
The definitions that we have given here are the ones usually used today; however, some authors switch the meanings of the two kinds of terms, or use all terms synonymously for only one condition.
In Wikipedia, we will use the terms "completely regular" and "Tychonoff" freely, but we'll avoid the less clear "T" terms.
In other literature, you should take care to find out which definitions the author is using.
(The phrase "completely regular Hausdorff", however, is unambiguous, and always means a Tychonoff space.)
For more on this issue, see History of the separation axioms
History of the separation axioms
In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...
.
Completely regular spaces and Tychonoff spaces are related through the notion of Kolmogorov equivalence.
A topological space is Tychonoff if and only if it's both completely regular and T0
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
.
On the other hand, a space is completely regular if and only if its Kolmogorov quotient is Tychonoff.
Examples and counterexamples
Almost every topological space studied in mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
is Tychonoff, or at least completely regular.
For example, the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is Tychonoff under the standard Euclidean topology
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Other examples include:
- Every metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is Tychonoff; every pseudometric spacePseudometric spaceIn mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
is completely regular. - Every locally compact regularRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
space is completely regular, and therefore every locally compact Hausdorff space is Tychonoff. - In particular, every topological manifoldTopological manifoldIn mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
is Tychonoff. - Every totally ordered set with the order topologyOrder topologyIn mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
is Tychonoff. - Every topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is completely regular. - Generalising both the metric spaces and the topological groups, every uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
is completely regular. The converse is also true: every completely regular space is uniformisable. - Every CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
is Tychonoff. - Every normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
regular space is completely regular, and every normal Hausdorff space is Tychonoff. - The Niemytzki plane is an example of a Tychonoff space which is not normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
.
Preservation
Completely regularity and the Tychonoff property are well-behaved with respect to initial topologiesInitial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
. Specifically, complete regularity is preserved by taking arbitrary initial topologies and the Tychonoff property is preserved by taking point-separating initial topologies. It follows that:
- Every subspace of a completely regular or Tychonoff space has the same property.
- A nonempty product space is completely regular (resp. Tychonoff) if and only if each factor space is completely regular (resp. Tychonoff).
Like all separation axioms, completely regularity is not preserved by taking final topologies
Final topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
. In particular, quotients
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of completely regular spaces need not be regular
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
. Quotients of Tychonoff spaces need not even be Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. There are closed quotients of the Moore plane
Moore plane
In mathematics, the Moore plane, also sometimes called Niemytzki plane is a topological space. It is a completely regular Hausdorff space which is not normal...
which provide counterexamples.
Real-valued continuous functions
For any topological space X, let C(X) denote the family of real-valued continuous functions on X and let C*(X) be the subset of boundedBounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
real-valued continuous functions.
Completely regular spaces can be characterized by the fact that their topology is completely determined by C(X) or C*(X). In particular:
- A space X is completely regular if and only if it has the initial topologyInitial topologyIn general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
induced by C(X) or C*(X). - A space X is completely regular if and only if every closed set can be written as the intersection of a family of zero sets in X (i.e. the zero sets form a basis for the closed sets of X).
- A space X is completely regular if and only if the cozero sets of X form a basis for the topology of X.
Given an arbitrary topological space (X, τ) there is a universal way of associating a completely regular space with (X, τ). Let ρ be the initial topology on X induced by Cτ(X) or, equivalently, the topology generated by the basis of cozero sets in (X, τ). Then ρ will be the finest completely regular topology on X which is coarser than τ. This construction is universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in the sense that any continuous function
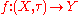
to a completely regular space Y will be continuous on (X, ρ). In the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
which sends (X, τ) to (X, ρ) is left adjoint to the inclusion functor CReg → Top. Thus the category of completely regular spaces CReg is a reflective subcategory
Reflective subcategory
In mathematics, a subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector...
of Top, the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. By taking Kolmogorov quotients, one sees that the subcategory of Tychonoff spaces is also reflective.
One can show that Cτ(X) = Cρ(X) in the above construction so that the rings C(X) and C*(X) are typically only studied for completely regular spaces X.
The category of real compact
Realcompact space
In mathematics, in the field of topology, a topological space is said to be realcompact if it is completely regular Hausdorff and every point of its Stone-Cech compactification is real...
Tychonoff spaces is anti-equivalent to the category of the rings C(X) (where X is real compact) together with ring homomorphisms as maps. For example one can reconstruct $X$ from C(X) when X is (real) compact. The algebraic theory of these rings is therefore subject of intensive studies.
A vast generalisation of this class of rings which still resembles many properties of Tychonoff spaces but is also applicable in real algebraic geometry
Real algebraic geometry
In mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....
, is the class of real closed ring
Real closed ring
In mathematics, a real closed ring is a commutative ring A thatis a subring of a product of real closed fields, which is closed undercontinuous semi-algebraic functions defined over the integers.- Examples of real closed rings :...
s.
Embeddings
Tychonoff spaces are precisely those spaces which can beembedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in compact Hausdorff spaces. More precisely, for every Tychonoff space X, there exists a compact Hausdorff space K such that X is homeomorphic to a subspace of K.
In fact, one can always choose K to be a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
(i.e. a possibly infinite product of unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
s). Every cube is compact Hausdorff as a consequence of Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
. Since every subspace of a compact Hausdorff space is Tychonoff one has:
- A topological space is Tychonoff if and only if it can be embedded in a cube.
Compactifications
Of particular interest are those embeddings where the image of X is dense in K; these are called Hausdorff compactificationCompactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
s of X. Given any embedding of a Tychonoff space X in a compact Hausdorff space K the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the image of X in K is a compactification of X.
Among those Hausdorff compactifications, there is a unique "most general" one, the Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
βX.
It is characterised by the universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
that, given a continuous map f from X to any other compact Hausdorff space Y, there is a unique continuous map g from βX to Y that extends f in the sense that f is the composition of g and j.
Uniform structures
Complete regularity is exactly the condition necessary for the existence of uniform structures on a topological space. In other words, every uniform spaceUniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
has a completely regular topology and every completely regular space X is uniformizable. A topological space admits a separated uniform structure if and only if it is Tychonoff.
Given a completely regular space X there is usually more than one uniformity on X that is compatible with the topology of X. However, there will always be a finest compatible uniformity, called the fine uniformity on X. If X is Tychonoff, then the uniform structure can be chosen so that βX becomes the completion of the uniform space X.

