
Induced topology
Encyclopedia
In topology
and related areas of mathematics
, an induced topology on a topological space
is a topology
which is "optimal" for some function
from/to this topological space.
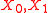 be sets,
be sets,  .
.
If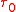 is a topology on
is a topology on 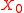 , then a topology induced on
, then a topology induced on  by
by 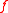 is
is 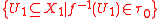 .
.
If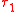 is a topology on
is a topology on 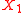 , then a topology induced on
, then a topology induced on 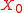 by
by 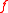 is
is 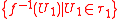 .
.
The easy way to remember the definitions above is to notice that finding an inverse image is used in both. This is because inverse image preserves union
and intersection
. Finding a direct image does not preserve intersection in general. Here is an example where this becomes a hurdle. Consider a set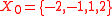 with a topology
with a topology 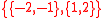 , a set
, a set 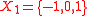 and a function
and a function  such that
such that  . A set of subsets
. A set of subsets  is not a topology, because
is not a topology, because 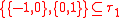 but
but 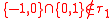 .
.
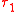 induced on
induced on 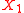 by
by 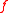 is the finest topology such that
is the finest topology such that  is continuous
is continuous  .
.
A topology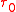 induced on
induced on 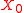 by
by  is the coarsest topology such that
is the coarsest topology such that 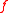 is continuous
is continuous  .
.
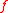 is an inclusion map
is an inclusion map
, then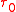 is a subspace topology
is a subspace topology
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an induced topology on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
which is "optimal" for some function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from/to this topological space.
Definition
Let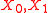 be sets,
be sets,  .
.If
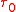 is a topology on
is a topology on 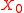 , then a topology induced on
, then a topology induced on  by
by 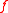 is
is 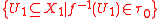 .
.If
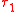 is a topology on
is a topology on 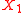 , then a topology induced on
, then a topology induced on 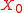 by
by 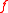 is
is 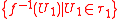 .
.The easy way to remember the definitions above is to notice that finding an inverse image is used in both. This is because inverse image preserves union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
and intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
. Finding a direct image does not preserve intersection in general. Here is an example where this becomes a hurdle. Consider a set
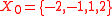 with a topology
with a topology 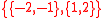 , a set
, a set 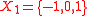 and a function
and a function  such that
such that  . A set of subsets
. A set of subsets  is not a topology, because
is not a topology, because 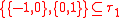 but
but 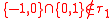 .
.Properties
A topology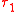 induced on
induced on 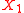 by
by 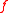 is the finest topology such that
is the finest topology such that  is continuous
is continuous  .
.A topology
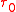 induced on
induced on 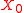 by
by  is the coarsest topology such that
is the coarsest topology such that 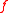 is continuous
is continuous  .
.Examples
In particular, if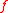 is an inclusion map
is an inclusion mapInclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
, then
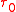 is a subspace topology
is a subspace topologySubspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
.

