
Rectangle
Encyclopedia
| Rectangle | |
|---|---|
| Family | Orthotope |
| Type | Quadrilateral Quadrilateral In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on... |
| Edges and vertices | 4 |
| Schläfli symbol | {}x{} |
| Symmetry group | D2, [2], (*22) |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| Dual polygon Dual polygon In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.-Properties:Regular polygons are self-dual.... |
Rhombus Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... |
| Properties | isogonal, convex Convex polygon In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set... , cyclic |
In Euclidean plane geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, a rectangle is any quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
with four right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s. The term "oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
ABCD would be denoted as .
The word rectangle comes from the Latin "rectangulus", which is a combination of "rectus" (right) and "angulus" (angle).
A so-called crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals. It is a special case of an antiparallelogram
Antiparallelogram
An antiparallelogram is a quadrilateral in which, like a parallelogram, the pairs of nonadjacent sides are congruent, but in which two opposite sides intersect and are therefore not parallel.-Properties:Every antiparallelogram has an axis of symmetry through its crossing point...
, and its angles are not right angles. Other geometries, such as spherical
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, elliptic
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, and hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, have so-called rectangles with opposite sides equal in length and equal angles that are not right angles.
Rectangles are involved in many tiling problems, such as tiling the plane by rectangles or tiling a rectangle by polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s.
Characterizations
A convex quadrilateralQuadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
is a rectangle if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is any one of the following:
- a parallelogram with at least one right angle
- an equiangular parallelogram
- a parallelogram with congruent diagonals
- a parallelogram ABCD where triangles ABD and DCA are congruent
- a quadrilateral which has four right angles
- an equiangular quadrilateral
Traditional hierarchy
A rectangle is a special case of a parallelogramParallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
in which each pair of adjacent sides is perpendicular.
A parallelogram, and hence also a rectangle, is a special case of a trapezium (known as a trapezoid
Trapezoid
In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
in North America) in which both pairs of opposite sides are parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
and equal in length.
A trapezium, and hence also a rectangle, is a convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
quadrilateral which has at least one pair of parallel opposite sides.
A convex quadrilateral, and hence also a rectangle, is
- Star-shapedStar-shaped polygonA star-shaped polygon is a polygonal region in the plane which is a star domain, i.e., a polygon P is star-shaped, if there exists a point z such that for each point p of P the segment zp lies entirely within P.The set of all points z with the described property is called the kernel of...
: The whole interior is visible from a single point, without crossing any edge. - SimpleSimple polygonIn geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
: The boundary does not cross itself.
Alternative hierarchy
De Villiers defines a rectangle more generally as any quadrilateral with axes of symmetryReflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
through each pair of opposite sides. This definition includes both right-angled rectangles and crossed rectangles. Each has an axis of symmetry parallel to and equidistant from a pair of opposite sides, and another which is the perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
bisector of those sides, but, in the case of the crossed rectangle, the first axis is not an axis of symmetry for either side that it bisects.
Quadrilaterals with two axes of symmetry, each through a pair of opposite sides, belong to the larger class of quadrilaterals with at least one axis of symmetry through a pair of opposite sides. These quadrilaterals comprise isosceles trapezia
Isosceles trapezoid
In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides, making it automatically a trapezoid...
and crossed isosceles trapezia (crossed quadrilaterals with the same vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
as isosceles trapezia).
Symmetry
A rectangle is cyclic: all corners lie on a single circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
It is equiangular
Equiangular polygon
In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon.The only equiangular triangle is the equilateral triangle...
: all its corner angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s are equal (each of 90 degrees
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
).
It is isogonal or vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
: all corners lie within the same symmetry orbit.
It has two lines of reflectional symmetry and rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
of order 2 (through 180°).
Rectangle-rhombus duality
The dual polygonDual polygon
In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.-Properties:Regular polygons are self-dual....
of a rectangle is a rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
, as shown in the table below.
| Rectangle | Rhombus |
|---|---|
| All angles are congruent. | All sides are congruent. |
| Its centre is equidistant from its vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... , hence it has a circumcircle. |
Its centre is equidistant from its sides, hence it has an incircle. |
| Its axes of symmetry bisect opposite sides. | Its axes of symmetry bisect opposite angles. |
Miscellaneous
The two diagonalDiagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
s are equal in length and bisect
Bisection
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...
each other. Every quadrilateral with both these properties is a rectangle.
A rectangle is rectilinear
Rectilinear polygon
A rectilinear polygon is a polygon all of whose edges meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons....
: its sides meet at right angles.
A non-square rectangle has 5 degrees of freedom
Degrees of freedom
Degrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
, comprising 2 for position, 1 for rotational orientation, 1 for overall size, and 1 for shape.
Two rectangles, neither of which will fit inside the other, are said to be incomparable
Comparability
In mathematics, any two elements x and y of a set P that is partially ordered by a binary relation ≤ are comparable when either x ≤ y or y ≤ x...
.
With vertices denoted A, B, C, and D, for any point P in the interior of a rectangle,
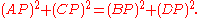
Formulas

 and width
and width 
- it has areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
 ,
, - it has perimeterPerimeterA perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
 ,
, - each diagonal has length
 ,
, - and when
 , the rectangle is a squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, the rectangle is a squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
.
Theorems
The isoperimetric theorem for rectangles states that among all rectangles of a given perimeter, the square has the largest area.The midpoints of the sides of any quadrilateral with perpendicular diagonals form a rectangle.
A parallelogram with equal diagonals is a rectangle.
The Japanese theorem for cyclic quadrilaterals states that the incentres of the four triangles determined by the vertices of a cyclic quadrilateral taken three at a time form a rectangle.
Crossed rectangles
A crossed (self-intersecting) quadrilateral consists of two opposite sides of a non-self-intersecting quadrilateral along with the two diagonals. Similarly, a crossed rectangle is a crossed quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals. It has the same vertex arrangementVertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
as the rectangle. It appears as two identical triangles with a common vertex, but the geometric intersection is not considered a vertex.
A crossed quadrilateral is sometimes likened to a bow tie
Bow tie
The bow tie is a type of men's necktie. It consists of a ribbon of fabric tied around the collar in a symmetrical manner such that the two opposite ends form loops. Ready-tied bow ties are available, in which the distinctive bow is sewn into shape and the band around the neck incorporates a clip....
or butterfly. A three-dimensional rectangular wire frame that is twisted can take the shape of a bow tie. A crossed rectangle is sometimes called an "angular eight".
The interior of a crossed rectangle can have a polygon density of +/-1 in each triangle, dependent upon the winding orientation as clockwise or counterclockwise.
A crossed rectangle is not equiangular. The sum of its interior angles (two acute and two reflex), as with any crossed quadrilateral, is 720°.
A rectangle and a crossed rectangle are quadrilaterals with the following properties in common:
- Opposite sides are equal in length.
- The two diagonals are equal in length.
- It has two lines of reflectional symmetry and rotational symmetry of order 2 (through 180°).
Other rectangles
In solid geometrySolid geometry
In mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...
, a figure is non-planar if it is not contained in a (flat) plane. A skew
Skew polygon
In geometry, a skew polygon is a polygon whose vertices do not lie in a plane. Skew polygons must have at least 4 vertices.A regular skew polygon is a skew polygon with equal edge lengths and which is vertex-transitive....
rectangle is a non-planar quadrilateral with opposite sides equal in length and four equal acute angles. A saddle rectangle is a skew rectangle with vertices that alternate an equal distance above and below a plane passing through its center, named for its minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
interior seen with saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
at its center. The convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of this skew rectangle is a special tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
called a rhombic disphenoid. (The term "skew rectangle" is also used in 2D graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
to refer to a distortion of a rectangle using a "skew" tool. The result can be a parallelogram or a trapezoid/trapezium
Trapezoid
In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
.)
In spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, a spherical rectangle is a figure whose four edges are great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
arcs which meet at equal angles greater than 90 degrees. Opposite arcs are equal in length. The surface of a sphere in Euclidean solid geometry is a non-Euclidean surface in the sense of elliptic geometry. Spherical geometry is the simplest form of elliptic geometry.
In elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, an elliptic rectangle is a figure in the elliptic plane whose four edges are elliptic arcs which meet at equal angles greater than 90 degrees. Opposite arcs are equal in length.
In hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, a hyperbolic rectangle is a figure in the hyperbolic plane whose four edges are hyperbolic arcs which meet at equal angles less than 90 degrees. Opposite arcs are equal in length.
Tessellations
The rectangle is used in many periodic tessellationTessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
patterns, in brickwork
Brickwork
Brickwork is masonry produced by a bricklayer, using bricks and mortar to build up brick structures such as walls. Brickwork is also used to finish corners, door, and window openings, etc...
, for example, these tilings:
Stacked bond |
 Running bond |
 Basket weave |
 Basket weave |
 Herringbone pattern Herringbone pattern The herringbone pattern is an arrangement of rectangles used for floor tilings and road pavement.The blocks can be rectangles or parallelograms... |
Squared, perfect, and other tiled rectangles
A rectangle tiled by squares, rectangles, or triangles is said to be a "squared", "rectangled", or "triangulated" (or "triangled") rectangle respectively. The tiled rectangle isperfect if the tiles are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
and finite in number and no two tiles are the same size. If two such tiles are the same size, the tiling is imperfect. In a perfect (or imperfect) triangled rectangle the triangles must be right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s.
A rectangle has commensurable
Commensurability (mathematics)
In mathematics, two non-zero real numbers a and b are said to be commensurable if a/b is a rational number.-History of the concept:...
sides if and only if it is tileable by a finite number of unequal squares. The same is true if the tiles are unequal isosceles right triangles.
The tilings of rectangles by other tiles which have attracted the most attention are those by congruent non-rectangular polyomino
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
es, allowing all rotations and reflections. There are also tilings by congruent polyabolo
Polyabolo
In recreational mathematics, a polyabolo is a polyform with an isosceles right triangle as the base form.The name is a back formation from 'diabolo' although the shape formed by joining two triangles at just one vertex is not a proper polyabolo...
es.
External links
- Definition and properties of a rectangle with interactive animation.
- Area of a rectangle with interactive animation.

