Bolzano–Weierstrass theorem
Encyclopedia
In real analysis
, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space
Rn. The theorem states that
each bounded sequence in Rn has a convergent
subsequence
. An equivalent formulation is that a subset of Rn is sequentially compact
if and only if it is closed
and bounded
.
Lemma: Every sequence { xn } in R has a monotone subsequence
.
Proof: Let us call a positive integer n a "peak of the sequence" if m > n implies i.e., if xn is greater than every subsequent term in the sequence. Suppose first that the sequence has infinitely many peaks, n1 < n2 < n3 < … < nj < …. Then the subsequence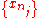
corresponding to peaks is monotonically decreasing, and we are done. So suppose now that there are only finitely many peaks, let N be the last peak and . Then n1 is not a peak, since , which implies the existence of an with 
Again, is not a peak, hence there is with 
Repeating this process leads to an infinite non-decreasing subsequence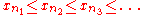 
, as desired.
Now suppose we have a bounded sequence in R; by the Lemma there exists a monotone subsequence, necessarily bounded. But it follows from the Monotone convergence theorem that this subsequence must converge, and the proof is complete.
Finally, the general case can be easily reduced to the case of n = 1 as follows: given a bounded sequence in Rn, the sequence of first coordinates is a bounded real sequence, hence has a convergent subsequence. We can then extract a subsubsequence on which the second coordinates converge, and so on, until in the end we have passed from the original sequence to a subsequence n times — which is still a subsequence of the original sequence — on which each coordinate sequence converges, hence the subsequence itself is convergent.
This form of the theorem makes especially clear the analogy to the Heine–Borel theorem
,
which asserts that a subset of Rn is compact if and only if it is closed and bounded. In fact, general topology tells us that a metrizable space is compact if and only if it is sequentially compact, so that the Bolzano–Weierstrass and Heine–Borel theorems are essentially the same.
and Karl Weierstrass
. It was actually first proved by Bolzano in 1817 as a lemma
in the proof of the intermediate value theorem
. Some fifty years later the result was identified as significant in its own right, and proved again by Weierstrass. It has since become an essential theorem of analysis
.
concepts in economics, the proofs of the existence of which often require variations of the Bolzano–Weierstrass theorem. One example is the existence of a Pareto efficient
allocation. An allocation is a matrix of consumption bundles for agents in an economy, and an allocation is Pareto efficient if no change can be made to it which makes no agent worse off and at least one agent better off (here rows of the allocation matrix must be rankable by a preference relation). The Bolzano–Weierstrass theorem allows one to prove that if the set of allocations is compact and non-empty, then the system has a Pareto-efficient allocation.
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. The theorem states that
each bounded sequence in Rn has a convergent
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
. An equivalent formulation is that a subset of Rn is sequentially compact
Sequentially compact space
In mathematics, a topological space is sequentially compact if every sequence has a convergent subsequence. For general topological spaces, the notions of compactness and sequential compactness are not equivalent; they are, however, equivalent for metric spaces....
if and only if it is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
.
Proof
First we prove the theorem when n = 1, in which case the ordering on R can be put to good use. Indeed we have the following result.Lemma: Every sequence { xn } in R has a monotone subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
.
Proof: Let us call a positive integer n a "peak of the sequence" if m > n implies i.e., if xn is greater than every subsequent term in the sequence. Suppose first that the sequence has infinitely many peaks, n1 < n2 < n3 < … < nj < …. Then the subsequence
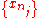corresponding to peaks is monotonically decreasing, and we are done. So suppose now that there are only finitely many peaks, let N be the last peak and . Then n1 is not a peak, since , which implies the existence of an with Again, is not a peak, hence there is with Repeating this process leads to an infinite non-decreasing subsequence 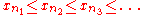, as desired.Now suppose we have a bounded sequence in R; by the Lemma there exists a monotone subsequence, necessarily bounded. But it follows from the Monotone convergence theorem that this subsequence must converge, and the proof is complete.
Finally, the general case can be easily reduced to the case of n = 1 as follows: given a bounded sequence in Rn, the sequence of first coordinates is a bounded real sequence, hence has a convergent subsequence. We can then extract a subsubsequence on which the second coordinates converge, and so on, until in the end we have passed from the original sequence to a subsequence n times — which is still a subsequence of the original sequence — on which each coordinate sequence converges, hence the subsequence itself is convergent.
Sequential compactness in Euclidean spaces
Suppose A is a subset of Rn with the property that every sequence in A has a subsequence converging to an element of A. Then A must be bounded, since otherwise there exists a sequence xm in A with || xm || ≥ m for all m, and then every subsequence is unbounded and therefore not convergent. Moreover A must be closed, since from a noninterior point x in the complement of A one can build an A-valued sequence converging to x. Thus the subsets A of Rn for which every sequence in A has a subsequence converging to an element of A – i.e., the subsets which are sequentially compact in the subspace topology – are precisely the closed and bounded sets.This form of the theorem makes especially clear the analogy to the Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
,
which asserts that a subset of Rn is compact if and only if it is closed and bounded. In fact, general topology tells us that a metrizable space is compact if and only if it is sequentially compact, so that the Bolzano–Weierstrass and Heine–Borel theorems are essentially the same.
History
The Bolzano–Weierstrass theorem is named after mathematicians Bernard BolzanoBernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
and Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
. It was actually first proved by Bolzano in 1817 as a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
in the proof of the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
. Some fifty years later the result was identified as significant in its own right, and proved again by Weierstrass. It has since become an essential theorem of analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
.
Application to economics
There are different important equilibriumEconomic equilibrium
In economics, economic equilibrium is a state of the world where economic forces are balanced and in the absence of external influences the values of economic variables will not change. It is the point at which quantity demanded and quantity supplied are equal...
concepts in economics, the proofs of the existence of which often require variations of the Bolzano–Weierstrass theorem. One example is the existence of a Pareto efficient
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
allocation. An allocation is a matrix of consumption bundles for agents in an economy, and an allocation is Pareto efficient if no change can be made to it which makes no agent worse off and at least one agent better off (here rows of the allocation matrix must be rankable by a preference relation). The Bolzano–Weierstrass theorem allows one to prove that if the set of allocations is compact and non-empty, then the system has a Pareto-efficient allocation.
See also
- Sequentially compact spaceSequentially compact spaceIn mathematics, a topological space is sequentially compact if every sequence has a convergent subsequence. For general topological spaces, the notions of compactness and sequential compactness are not equivalent; they are, however, equivalent for metric spaces....
- Heine–Borel theoremHeine–Borel theoremIn the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
- Fundamental axiom of analysis