
Continuous functions on a compact Hausdorff space
Encyclopedia
In mathematical analysis
, and especially functional analysis
, a fundamental role is played by the space of continuous functions on a compact
Hausdorff space
with values in the real or complex numbers. This space, denoted by C(X), is a vector space
with respect to the pointwise addition of functions and scalar multiplication by constants. It is, moreover, a normed space with norm defined by
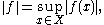
the uniform norm. The uniform norm defines the topology
of uniform convergence of functions on X. The space C(X) is a Banach space
with respect to this norm.
It is sometimes desirable, particularly in measure theory, to further refine this general definition by considering the special case when X is a locally compact Hausdorff space. In this case, it is possible to identify a pair of distinguished subsets of CB(X):
The closure of C00(X) is precisely C0(X). In particular, the latter is a Banach space.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, and especially functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a fundamental role is played by the space of continuous functions on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
with values in the real or complex numbers. This space, denoted by C(X), is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with respect to the pointwise addition of functions and scalar multiplication by constants. It is, moreover, a normed space with norm defined by
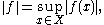
the uniform norm. The uniform norm defines the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of uniform convergence of functions on X. The space C(X) is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
with respect to this norm.
Properties
- By Urysohn's lemmaUrysohn's lemmaIn topology, Urysohn's lemma is a lemma that states that a topological space is normal if and only if any two disjoint closed subsets can be separated by a function....
, C(X) separates pointsSeparating setIn mathematics a set of functions S from a set D to a set C is called a separating set for D or said to separate the points of D if for any two distinct elements x and y of D, there exists a function f in S so that f ≠ f.- Examples :* The singleton set consisting of the identity function on R...
of X: If x, y ∈ X and x ≠ y, then there is an f ∈ C(X) such that f(x) ≠ f(y).
- The space C(X) is infinite-dimensional whenever X is an infinite space (since it separates points). Hence, in particular, it is generally not locally compact.
- C(X), with its uniform norm, is a commutative Banach algebra with identity.
- The Riesz representation theoremRiesz representation theoremThere are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
gives a characterization of the continuous dual space of C(X). Specifically, this dual space is the space of Radon measureRadon measureIn mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
s on X (regular Borel measures), denoted by rca(X). This space, with the norm given by the total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of a measure, is also a Banach space belonging to the class of ba spaceBa spaceIn mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|....
s.
- Positive linear functionalPositive linear functionalIn mathematics, especially in functional analysis, a positive linear functional on an ordered vector space is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds thatf\geq 0....
s on C(X) correspond to (positive) regularRegular measureIn mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".-Definition:...
Borel measures on X, by a different form of the Riesz representation theorem.
- If X is infinite, then C(X) is not reflexiveReflexive spaceIn functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
, nor is it weaklyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
.
- The Arzelà-Ascoli theoremArzelà-Ascoli theoremIn mathematics, the Arzelà–Ascoli theorem of functional analysis gives necessary and sufficient conditions to decide whether every subsequence of a given sequence of real-valued continuous functions defined on a closed and bounded interval has a uniformly convergent subsequence. The main condition...
holds: A subset K of C(X) is relatively compact if and only if it is boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
in the norm of C(X), and equicontinuous.
- The Stone-Weierstrass theoremStone-Weierstrass theoremIn mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
holds for C(X). In the case of real functions, if A is a subringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of C(X) that contains all constants and separates points, then the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of A is C(X). In the case of complex functions, the statement holds with the additional hypothesis that A is closed under complex conjugation.
- If X and Y are two compact Hausdorff spaces, and F : C(X) → C(Y) is a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of algebras which commutes with complex conjugation, then F is continuous. Furthermore, F has the form F(h)(y) = h(f(x)) for some continuous function ƒ : X → Y. In particular, if C(X) and C(Y) are isomorphic as algebras, then X and Y are homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
topological spaces.
- Let Δ be the space of maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s in C(X). Then there is a one-to-one correspondence between Δ and the points of X. Furthermore Δ can be identified with the collection of all complex homomorphisms C(X) → C. Equip Δ with the initial topologyInitial topologyIn general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
with respect to this pairing with C(X) (i.e., the Gelfand transform). Then X is homeomorphic to Δ equipped with this topology.
- A sequence in C(X) is weaklyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
CauchyCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
if and only if it is (uniformly) bounded in C(X) and pointwise convergent. In particular, C(X) is only weakly complete for X a finite set.
- The vague topologyVague topologyIn mathematics, particularly in the area of functional analysis and topological vector spaces, the vague topology is an example of the weak-* topology which arises in the study of measures on locally compact Hausdorff spaces....
is the weak* topology on the dual of C(X).
- The Banach–Alaoglu theorem implies that any normed space is isometrically isomorphic to a subspace of C(X) for some X.
Generalizations
The space C(X) of real or complex-valued continuous functions can be defined on any topological space X. In the non-compact case, however, C(X) is not in general a Banach space with respect to the uniform norm since it may contain unbounded functions. Hence it is more typical to consider the space, denoted here CB(X) of bounded continuous functions on X. This is a Banach space (in fact a commutative Banach algebra with identity) with respect to the uniform norm.It is sometimes desirable, particularly in measure theory, to further refine this general definition by considering the special case when X is a locally compact Hausdorff space. In this case, it is possible to identify a pair of distinguished subsets of CB(X):
- C00(X), the subset of C(X) consisting of functions with compact support. This is called the space of functions vanishing in a neighborhood of infinity.
- C0(X), the subset of C(X) consisting of functions such that for every ε > 0, there is a compact set K⊂X such that |f(x)| < ε for all x ∈ X\K. This is called the space of functions vanishing at infinity.
The closure of C00(X) is precisely C0(X). In particular, the latter is a Banach space.

