Peano existence theorem
Encyclopedia
In mathematics
, specifically in the study of ordinary differential equation
s, the Peano existence theorem, Peano theorem or Cauchy-Peano theorem, named after Giuseppe Peano
and Augustin Louis Cauchy
, is a fundamental theorem
which guarantees the existence
of solutions to certain initial value problem
s.
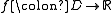
a continuous function and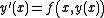
a continuous
, explicit first-order differential equation defined on D, then every initial value problem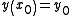
for f with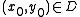
has a local solution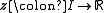
where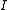
is a neighbourhood
of x0,
such that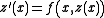
for all 
.
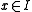Note that the solution need not be unique: one and the same initial value (x0,y0) may give rise to many different solutions z.
s.
. The Picard–Lindelöf theorem both assumes more and concludes more. It requires Lipschitz continuity, while the Peano theorem requires only continuity; but it proves both existence and uniqueness where the Peano theorem proves only the existence of solutions. To illustrate, consider the ordinary differential equation
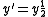on the domain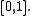 
According to the Peano theorem, this equation has solutions, but the Picard-Lindelöf theorem does not apply since the right hand side is not Lipschitz continuous in any neighbourhood containing 0. Thus we can conclude existence but not uniqueness. It turns out that this ordinary differential equation has two kinds of solutions when starting at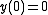
, either 
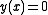or 
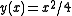. The transition between 
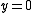and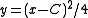 
can happen at any C.
The Carathéodory existence theorem
is a generalization of the Peano existence theorem with weaker conditions than continuity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in the study of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, the Peano existence theorem, Peano theorem or Cauchy-Peano theorem, named after Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
and Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
, is a fundamental theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
which guarantees the existence
Existence
In common usage, existence is the world we are aware of through our senses, and that persists independently without them. In academic philosophy the word has a more specialized meaning, being contrasted with essence, which specifies different forms of existence as well as different identity...
of solutions to certain initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
s.
History
Peano first published the theorem in 1886 with an incorrect proof. In 1890 he published a new correct proof using successive approximations.Theorem
Let D be an open subset of R × R with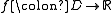a continuous function and
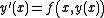
a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, explicit first-order differential equation defined on D, then every initial value problem
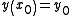
for f with
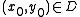
has a local solution
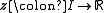
where
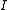is a neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of x0,
such that
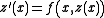for all 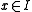.Note that the solution need not be unique: one and the same initial value (x0,y0) may give rise to many different solutions z.
Extensions
The theorem holds as stated for explicit first order systems also in higher dimensions, when D is an open subset of R × Rn. It is however in general wrong for differential equations in infinite-dimensional Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.
Related theorems
The Peano theorem can be compared with another existence result in the same context, the Picard–Lindelöf theoremPicard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
. The Picard–Lindelöf theorem both assumes more and concludes more. It requires Lipschitz continuity, while the Peano theorem requires only continuity; but it proves both existence and uniqueness where the Peano theorem proves only the existence of solutions. To illustrate, consider the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
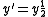on the domain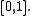 According to the Peano theorem, this equation has solutions, but the Picard-Lindelöf theorem does not apply since the right hand side is not Lipschitz continuous in any neighbourhood containing 0. Thus we can conclude existence but not uniqueness. It turns out that this ordinary differential equation has two kinds of solutions when starting at
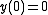, eithe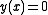r or 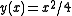. The transition between 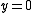and 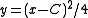can happen at any C.The Carathéodory existence theorem
Carathéodory's existence theorem
In mathematics, Carathéodory's existence theorem says that an ordinary differential equation has a solution under relatively mild conditions. It is a generalization of Peano's existence theorem...
is a generalization of the Peano existence theorem with weaker conditions than continuity.