In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 X is said to be limit point compact or weakly countably compact if every infinite subset of X has a limit point

Limit point

In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...

 in X. This property generalizes a property of compact spaces. In a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

, limit point compactness, compactness, and sequential compactness are all equivalent. For general topological spaces, however, these three notions of compactness are not equivalent.

Properties and Examples

• Limit point compactness is equivalent to countable compactness if X is a T₁-space and is equivalent to compactness
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
   if X is a metric space
  Metric space
  In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
  
  .

• An example of a space X that is not weakly countably compact is any countable (or larger) set with the discrete topology. A more interesting example is the countable complement topology.

• Even though a continuous function
  Continuous function
  In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
  
   from a compact space X, to an ordered set Y in the order topology, must be bounded, the same thing does not hold if X is limit point compact. An example is given by the space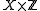 (where X = {1, 2} carries the indiscrete topology and is the set of all integers carrying the discrete topology) and the function given by projection onto the second coordinate. Clearly, ƒ is continuous and is limit point compact (in fact, every nonempty subset of 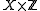has a limit point) but ƒ is not bounded
  Bounded function
  In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
  
  , and in fact is not even limit point compact.

• Every countably compact space (and hence every compact space) is weakly countably compact, but the converse is not true.

• For metrizable spaces, compactness, limit point compactness, and sequential compactness
  Sequentially compact space
  In mathematics, a topological space is sequentially compact if every sequence has a convergent subsequence. For general topological spaces, the notions of compactness and sequential compactness are not equivalent; they are, however, equivalent for metric spaces....
  
   are all equivalent.

• The set of all real numbers, R, is not limit point compact; the integers are an infinite set but do not have a limit point in R.

• If (X, T) and (X, T*) are topological spaces with T* finer than T and (X, T*) is limit point compact, then so is (X, T).

• A finite space is vacuously
  Vacuous truth
  A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
  
   limit point compact.

See also

• Compact space
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
  
• Sequential compactness
• Metric space
  Metric space
  In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
  
  
• Bolzano-Weierstrass theorem