
Pathological (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
.
Often, when the usefulness of a theorem is challenged by counterexamples, defenders of the theorem argue that the exceptions are pathological. A famous case is the Alexander horned sphere
Alexander horned sphere
The Alexander horned sphere is a wild embedding of a sphere into space, discovered by . It is the particular embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:...
, a counterexample showing that topologically embedding the sphere S2 in R3 may fail to "separate the space cleanly", unless an extra condition of tameness
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
is used to suppress possible wild behaviour. See Jordan-Schönflies theorem.
One can therefore say that (particularly in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
) those searching for the "pathological" are like experimentalist
Experimentalist
"Experimentalist" is a blanket term for all sorts of scientists engaged more in experimental activity than in the theoretical side of their sciences....
s, interested in knocking down potential theorems, in contrast to finding general statements widely applicable. Each activity has its role within mathematics.
Pathological functions
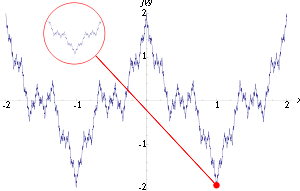
A classic example is the Weierstrass functionWeierstrass function
In mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere...
, which is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
everywhere but differentiable nowhere. The sum of a differentiable function and the Weierstrass function is again continuous but nowhere differentiable; so there are at least as many such functions as differentiable functions. In fact, by the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
one can show that continuous functions are typically or generically nowhere differentiable.
In layman's terms, this is because of the vast infinity of possible functions, relatively few will ever be studied by mathematicians, and those that do come to their attention as being interesting or useful will tend to be well-behaved. To quote Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
:
This highlights the fact that the term pathological is subjective or at least context-dependent, and its meaning in any particular case resides in the community of mathematicians, not necessarily within the subject matter of mathematics itself.
Prevalence
In cases of pathology, often "most" or "almost all" examples of a phenomenon are pathological, which is formalized by measures of size such as cardinality, measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
(almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
), probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
(almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
), or a generic property
Generic property
In mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
. For example, the set of rational numbers is countable (and has measure zero, and is a meagre set
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
), but the set of irrational numbers is uncountable (and has full measure, and is a comeagre set): "almost all" real numbers are irrational, in these senses.
In this case, pathologies are not the rare exceptions but the most common. This is why finding pathological examples are so important: far from being relegated to the fringe of our thought, they should serve to guide our mathematical intuition.
Pathological examples
Pathological examples often have some undesirable or unusual properties that make it difficult to contain or explain within a theory. Such pathological behaviour often prompts new investigation which leads to new theory and more general results. For example, five important historical examples of this are the following:- The discovery of irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s by the school of PythagorasPythagorasPythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
in ancient Greece; for example, the length of the diagonal of a unit squareUnit squareIn mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
, that is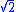
- The discovery of number fields whose rings of integersRing of integersIn mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
do not form a unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
, for example the field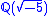 .
. - The discovery of fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s and other "rough" geometric objects (see Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
). - Weierstrass functionWeierstrass functionIn mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere...
, a realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function on the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, that is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
everywhere but differentiable nowhere. - Test functions in Fourier analysis, which are complex-valued functions on the real line, that are 0 everywhere outside of a given limited intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(hence all derivatives will also be 0 outside of the interval) and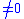 inside of the interval, but are still infinitely differentiable everywhere. An example of such a function is the test function
inside of the interval, but are still infinitely differentiable everywhere. An example of such a function is the test function
- The Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is a counterexample to the notion that a measure-zero set must be countable. The Cantor set is both measure-zero (i.e. has "length" 0) and uncountable. - The Dirichlet function is the function f defined such that f(x) is 1 if x is rational and 0 if x is irrational. This is a counterexample to the idea that every bounded function is (piecewise) integrable.
At the time of their discovery, each of these was considered highly pathological; today, each has been assimilated, which is to say, explained by an extensive general theory. These examples prompt us to reassess our foundational definitions and concepts. Historically, this has led to cleaner, more precise, and more powerful mathematics.
Such judgments about what is or is not pathological are inherently subjective or at least vary with context and depend on both training and experience—what is pathological to one researcher may very well be standard behaviour to another.
Pathological examples can show the importance of the assumptions in a theorem. For example, in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
does not satisfy the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, even though its symmetric bell-shape appears similar to many distributions which do; it fails the requirement to have a mean and standard deviation which exist and are finite.
The best-known paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es such as the Banach–Tarski paradox
Banach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
and Hausdorff paradox
Hausdorff paradox
In mathematics, the Hausdorff paradox, named after Felix Hausdorff, states that if you remove a certain countable subset of the sphere S2, the remainder can be divided into three disjoint subsets A, B and C such that A, B, C and B ∪ C are all congruent...
are based on the existence of non-measurable set
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
s. Mathematicians, unless they take the minority position of denying the axiom of choice, are in general resigned to living with such sets.
Other examples include the Peano space-filling curve
Space-filling curve
In mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
which maps the unit interval [0, 1] continuously onto [0, 1] × [0, 1], and the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, which is a subset of the interval [0, 1] and has the pathological property that it is uncountable, yet its measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
is zero.
Computer science
In computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, pathological has a slightly different sense with regard to the study of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s. Here, an input (or set of inputs) is said to be pathological if it causes atypical behavior from the algorithm, such as a violation of its average case complexity
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, or even its correctness. For example, hash table
Hash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
s generally have pathological inputs: sets of keys that collide
Hash collision
Not to be confused with wireless packet collision.In computer science, a collision or clash is a situation that occurs when two distinct pieces of data have the same hash value, checksum, fingerprint, or cryptographic digest....
on hash values. Quicksort normally has O(n log n)
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
time complexity, but deteriorates to O(n2) when given input that triggers suboptimal behaviour.
The term is often used pejoratively, as a way of dismissing such inputs as being specially designed to break a routine that is otherwise sound in practice (compare with Byzantine). On the other hand, awareness of pathological inputs is important as they can be exploited to mount a denial-of-service attack
Denial-of-service attack
A denial-of-service attack or distributed denial-of-service attack is an attempt to make a computer resource unavailable to its intended users...
on a computer system. Also, the term in this sense is a matter of subjective judgment as with its other senses. Given enough run time, a sufficiently large and diverse user community, or other factors, an input which may be dismissed as pathological could in fact occur (as seen in the first test flight
Ariane 5 Flight 501
Cluster was a constellation of four European Space Agency spacecraft which were launched on the maiden flight of the Ariane 5 rocket, Flight 501, and subsequently lost when that rocket failed to achieve orbit. The launch, which took place on Tuesday, June 4, 1996, ended in failure due to an error...
of the Ariane 5
Ariane 5
Ariane 5 is, as a part of Ariane rocket family, an expendable launch system used to deliver payloads into geostationary transfer orbit or low Earth orbit . Ariane 5 rockets are manufactured under the authority of the European Space Agency and the Centre National d'Etudes Spatiales...
).
Exceptions
A similar but distinct phenomenon is that of exceptional objectExceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
s (and exceptional isomorphism
Exceptional isomorphism
In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members ai and bj of two families of mathematical objects, that is not an example of a pattern of such isomorphisms.Because these series of objects are presented differently, they are not...
s), which occurs when there are a "small" number of exceptions to a general pattern – quantitatively, a finite set of exceptions to an otherwise infinite rule. By contrast, in cases of pathology, often most or all most all instances of a phenomenon are pathological, as discussed in prevalence, above – e.g., almost all real numbers are irrational.
Subjectively, exceptional objects (such as the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
or sporadic simple groups) are generally considered "beautiful", unexpected examples of a theory, while pathological phenomena are often considered "ugly", as the name implies. Accordingly, theories are usually expanded to include exceptional objects – for example, the exceptional Lie algebras are included in the theory of semisimple Lie algebras: the axioms are seen as good, the exceptional objects as unexpected but valid. By contrast, pathological examples are instead taken to point out a shortcoming in the axioms, requiring stronger axioms to rule them out – for example, requiring tameness of an embedding of a sphere in the Schönflies problem
Schönflies problem
In mathematics, the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies.-Original formulation:...
. One may study the more general theory, including the pathologies, which may provide its own simplifications (the real numbers have properties very different from the rationals, and likewise continuous maps have very different properties from smooth ones), but will also in general study the narrower theory from which the original examples were drawn.
External links
- Pathological Structures & Fractals - Extract of an article by Freeman DysonFreeman DysonFreeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
, "Characterising Irregularity", Science, May 1978

