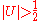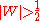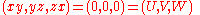Roman surface - AbsoluteAstronomy.com

The Roman surface is a self-intersecting mapping of the real projective plane

Real projective plane

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...

into three-dimensional space, with an unusually high degree of symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

. This mapping is not an immersion of the projective plane; however the figure resulting from removing six singular points is one.

The simplest construction is as the image of a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

centered at the origin under the map f(x,y,z) = (yz,xz,xy). This gives an implicit formula

Formula

In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....

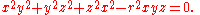
Also, taking a parametrization of the sphere in terms of longitude

Longitude

Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....

(θ) and latitude

Latitude

In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...

(φ), gives parametric equations for the Roman surface as follows:

x = r² cos θ cos φ sin φ

y = r² sin θ cos φ sin φ

z = r² cos θ sin θ cos² φ

The origin is a triple point, and each of the xy-, yz-, and xz-planes are tangential to the surface there. The other places of self-intersection are double points, defining segments along each coordinate axis which terminate in six pinch points. The entire surface has tetrahedral

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

symmetry

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

. It is a particular type (called type 1) of Steiner surface

Steiner surface

In geometry, a branch of mathematics, the Steiner surfaces, discovered by Jakob Steiner, are mappings of the real projective plane into three-dimensional real projective space...

, that is, a 3-dimensional linear projection of the Veronese surface

Veronese surface

In mathematics, the Veronese surface is an algebraic surface in five-dimensional projective space, and is realized by the Veronese embedding, the embedding of the projective plane given by the complete linear system of conics. It is named after Giuseppe Veronese...

Derivation of implicit formula

For simplicity we consider only the case r = 1. Given the sphere defined by the points (x, y, z) such that

we apply to these points the transformation T defined by

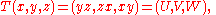
say.

But then we have

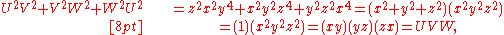
and so

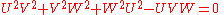
as desired.

Conversely, suppose we are given (U, V, W) satisfying

(*)

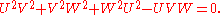
We prove that there exists (x,y,z) such that

(**)

for which

with one exception: In case 3.b. below, we show this cannot be proved.

1. In the case where none of U, V, W is 0, we can set

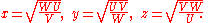
(Note that (*) guarantees that either all three of U, V, W are positive, or else exactly two are negative. So these square roots are of positive numbers.)

It is easy to use (*) to confirm that (**) holds for x, y, z defined this way.

2. Suppose that W is 0. From (*) this implies

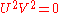
and hence at least one of U, V must be 0 also. This shows that is it impossible for exactly one of U, V, W to be 0.

3. Suppose that exactly two of U, V, W are 0. Without loss of generality

Without loss of generality

Without loss of generality is a frequently used expression in mathematics...

we assume

(***)

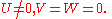
It follows that

(since

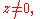
implies that

and hence

contradicting (***).)

a. In the subcase where

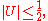
if we determine x and y by

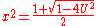
and

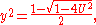
this ensures that (*) holds. It is easy to verify that

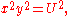
and hence choosing the signs of x and y appropriately will guarantee

Since also

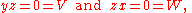
this shows that this subcase leads to the desired converse.

b. In this remaining subcase of the case 3., we have

Since

it is easy to check that

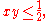
and thus in this case, where

there is no (x, y, z) satisfying

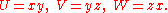
Hence the solutions (U, 0, 0) of the equation (*) with

and likewise, (0, V, 0) with

and (0, 0, W) with

(each of which is a noncompact portion of a coordinate axis, in two pieces) do not correspond to any point on the Roman surface.

4. If (U, V, W) is the point (0, 0, 0), then if any two of x, y, z are zero and the third one has absolute value 1, clearly

as desired.

This covers all possible cases.

Derivation of parametric equations

Let a sphere have radius r, longitude φ, and latitude θ. Then its parametric equations are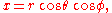

Then, applying transformation T to all the points on this sphere yields

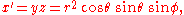
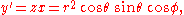
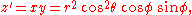
which are the points on the Roman surface. Let φ range from 0 to 2π, and let θ range from 0 to π/2.

Relation to the real projective plane

The sphere, before being transformed, is not homeomorphic

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

to the real projective plane, RP². But the sphere centered at the origin has this property, that if point (x,y,z) belongs to the sphere, then so does the antipodal point (-x,-y,-z) and these two points are different: they lie on opposite sides of the center of the sphere.

The transformation T converts both of these antipodal points into the same point,

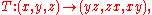
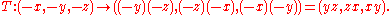
If this were true for only one or small subset of points of the sphere, then these points would just be double points. But since it is true of all points, then it is possible to consider the Roman surface to be homeomorphic to a "sphere modulo antipodes". However, these are not the only identifications that occur under this map. Consequently, the Roman surface is a quotient of the real projective plane RP² = S² / (x~-x). Furthermore, this quotient has the special property that it is locally injective, making this an immersion of RP² into 3-space. It was previously stated that the Roman surface is homeomorphic to RP², but this was in error.

Structure of the Roman surface

The Roman surface has four bulbous "lobes", each one on a different corner of a tetrahedron.

A Roman surface can be constructed by splicing together three hyperbolic paraboloids

Paraboloid

In mathematics, a paraboloid is a quadric surface of special kind. There are two kinds of paraboloids: elliptic and hyperbolic. The elliptic paraboloid is shaped like an oval cup and can have a maximum or minimum point....

and then smoothing out the edges as necessary so that it will fit a desired shape (e.g. parametrization).

Let there be these three hyperbolic paraboloids:

x = yz,
y = zx,
z = xy.

These three hyperbolic paraboloids intersect externally along the six edges of a tetrahedron and internally along the three axes. The internal intersections are loci of double points. The three loci of double points: x = 0, y = 0, and z = 0, intersect at a triple point at the origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

.

For example, given x = yz and y = zx, the second paraboloid is equivalent to x = y/z. Then

and either y = 0 or z² = 1 so that z = ±1. Their two external intersections are

x = y, z = 1;
x = −y, z = −1.

Likewise, the other external intersections are

x = z, y = 1;
x = −z, y = −1;
y = z, x = 1;
y = −z, x = −1.

Let us see the pieces being put together. Join the paraboloids y = xz and x = yz. The result is shown in Figure 1.

Figure 1.

The paraboloid y = x z is shown in blue and orange. The paraboloid x = y z is shown in cyan and purple. In the image the paraboloids are seen to intersect along the z = 0 axis. If the paraboloids are extended, they should also be seen to intersect along the lines

z = 1, y = x;
z = −1, y = −x.

The two paraboloids together look like a pair of orchids joined back-to-back.

Now run the third hyperbolic paraboloid, z = xy, through them. The result is shown in Figure 2.

Figure 2.

On the west-southwest and east-northeast directions in Figure 2 there are a pair of openings. These openings are lobes and need to be closed up. When the openings are closed up, the result is the Roman surface shown in Figure 3.

Figure 3. Roman surface.

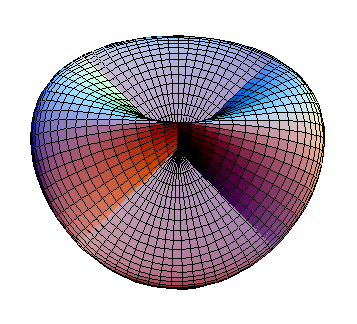A pair of lobes can be seen in the West and East directions of Figure 3. Another pair of lobes are hidden underneath the third (z = xy) paraboloid and lie in the North and South directions.

If the three intersecting hyperbolic paraboloids are drawn far enough that they intersect along the edges of a tetrahedron, then the result is as shown in Figure 4.

Figure 4.

One of the lobes is seen frontally—head on—in Figure 4. The lobe can be seen to be one of the four corners of the tetrahedron.

If the continuous surface in Figure 4 has its sharp edges rounded out—smoothed out—then the result is the Roman surface in Figure 5.

Figure 5. Roman surface.

One of the lobes of the Roman surface is seen frontally in Figure 5, and its bulbous – balloon-like—shape is evident.

If the surface in Figure 5 is turned around 180 degrees and then turned upside down, the result is as shown in Figure 6.

Figure 6. Roman surface.

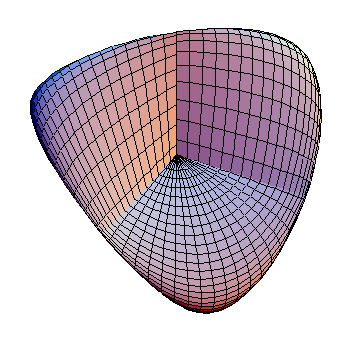Figure 6 shows three lobes seen sideways. Between each pair of lobes there is a locus of double points corresponding to a coordinate axis. The three loci intersect at a triple point at the origin. The fourth lobe is hidden and points in the direction directly opposite from the viewer. The Roman surface shown at the top of this article also has three lobes in sideways view.

One-sidedness

The Roman surface is non-orientable, i.e. one-sided. This is not quite obvious. To see this, look again at Figure 3.

Imagine an ant

Ant

Ants are social insects of the family Formicidae and, along with the related wasps and bees, belong to the order Hymenoptera. Ants evolved from wasp-like ancestors in the mid-Cretaceous period between 110 and 130 million years ago and diversified after the rise of flowering plants. More than...

on top of the "third" hyperbolic paraboloid, z = x y. Let this ant move North. As it moves, it will pass through the other two paraboloids, like a ghost passing through a wall. These other paraboloids only seem like obstacles due to the self-intersecting nature of the immersion. Let the ant ignore all double and triple points and pass right through them. So the ant moves to the North and falls off the edge of the world, so to speak. It now finds itself on the northern lobe, hidden underneath the third paraboloid of Figure 3. The ant is standing upside-down, on the "outside" of the Roman surface.

Let the ant move towards the Southwest. It will climb a slope (upside-down) until it finds itself "inside" the Western lobe. Now let the ant move in a Southeastern direction along the inside of the Western lobe towards the z = 0 axis, always above the x-y plane. As soon as it passes through the z = 0 axis the ant will be on the "outside" of the Eastern lobe, standing rightside-up.

Then let it move Northwards, over "the hill", then towards the Northwest so that it starts sliding down towards the x = 0 axis. As soon as the ant crosses this axis it will find itself "inside" the Northern lobe, standing right side up. Now let the ant walk towards the North. It will climb up the wall, then along the "roof" of the Northern lobe. The ant is back on the third hyperbolic paraboloid, but this time under it and standing upside-down. (Compare with Klein bottle

Klein bottle

In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...

Double, triple, and pinching points

The Roman surface has four "lobes". The boundaries of each lobe are a set of three lines of double points. Between each pair of lobes there is a line of double points. The surface has a total of three lines of double points, which lie (in the parametrization given earlier) on the coordinate axes. The three lines of double points intersect at a triple point which lies on the origin. The triple point cuts the lines of double points into a pair of half-lines, and each half-line lies between a pair of lobes. One might expect from the preceding statements that there could be up to eight lobes, one in each octant of space which has been divided by the coordinate planes. But the lobes occupy alternating octants: four octants are empty and four are occupied by lobes.

If the Roman surface were to be inscribed inside the tetrahedron with least possible volume, one would find that each edge of the tetrahedron is tangent to the Roman surface at a point, and that each of these six points happens to be a Whitney singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...

. These singularities, or pinching points, all lie at the edges of the three lines of double points, and they are defined by this property: that there is no plane tangent

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

to surface at the singularity.

External links

Coffman Steiner Surfaces, English
Roman Surfaces at the National Curve Bank (website of the California State University)
Ashay Dharwadker, Heptahedron and Roman Surface, Electronic Geometry Models, 2004.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.