Fundamental polygon
Encyclopedia
In mathematics
, each closed surface
in the sense of geometric topology
can be constructed from an even-sided oriented polygon
, called a fundamental polygon, by pairwise identification of its edges.
This construction can be represented as a string of length 2n of n distinct symbols where each symbol appears twice with exponent either +1 or −1. The exponent −1 signifies that the corresponding edge has the orientation opposing the one of the fundamental polygon.
. Then, the polygon, written in terms of group elements, becomes a constraint on the free group
generated by the edges, giving a group presentation with one constraint.
Thus, for example, given the Euclidean plane
, let the group element 
act on the plane as 
while 
. Then 
generate the lattice
, and the torus is given by the quotient space
(a homogeneous space
)
. More generally, the two generators 
can be taken to generate a parallelogram tiling, of fundamental parallelograms.
For the torus, the constraint on the free group in two letters is given by
. This constraint is trivially embodied in the action on the plane given above. Alternately, the plane can be tiled by hexagons, and the centers of the hexagons form a hexagonal lattice. Identifying opposite edges of the hexagon again leads to the torus, this time, with the constraint 
describing the action of the hexagonal lattice
generators on the plane.
In practice, most of the interesting cases are surfaces with negative curvature, and are thus realized by a discrete lattice
in the group 
acting on the upper half-plane. Such lattices are known as Fuchsian group
s.
n has the following standard fundamental polygon:
This fundamental polygon can be viewed as the result of glueing n tori together, and hence the surface is sometimes called the n-fold torus. ("Glueing" two surfaces means cutting a disk out of each and identifying the circular boundaries of the resulting holes.)
A non-orientable closed surface of (non-orientable) genus n has the following standard fundamental polygon:
Alternately, the non-orientable surfaces can be given in one of two forms, as n Klein bottle
s glued together (this may be called the n-fold Klein bottle, with non-orientable genus 2n), or as n glued real projective plane
s (the n-fold crosscap, with non-orientable genus n). The n-fold Klein bottle is given by the 4n-sided polygon
(note the final
is missing the superscript −1; this flip, as compared to the orientable case, being the source of the non-orientability). The 2n+1-fold crosscap is given by the 4n+2-sided polygon
That these two cases exhaust all the possibilities for a compact non-orientable surface was shown by Henri Poincaré
.
Riemann surface
has a number of important properties that relate the surface to its Fuchsian model
. That is, a hyperbolic compact Riemann surface has the upper half-plane as the universal cover, and can be represented as a quotient manifold
H/Γ where Γ is a non-Abelian group isomorphic to the deck transformation group of the surface. The cosets of the quotient space have the standard fundamental polygon as a representative element. In the following, note that all Riemann surfaces are orientable.
in the upper half-plane H, and a discrete subgroup
Γ of PSL(2,R) that acts freely discontinuously
on the upper half-plane, then one can define the metric fundamental polygon as the set of points
Here, d is a hyperbolic metric
on the upper half-plane. The metric fundamental polygon is more usually called the Dirichlet region or the Voronoi polygon.
The above construction is sufficient to guarantee that each side of the polygon is a closed (non-trivial) loop in the manifold H/Γ. As such, each side can thus an element of the fundamental group
. In particular, the fundamental group 
has 2n generators 
, with exactly one defining constraint,
.
The genus of the resulting manifold H/Γ is n.
is a fundamental parallelogram. By contrast, the metric fundamental polygon is six-sided, a hexagon. This can be most easily seen by noting that the sides of the hexagon are perpendicular bisectors of the edges of the parallelogram. That is, one picks a point in the lattice, and then considers the set of straight lines joining this point to nearby neighbors. Bisecting each such line by another perpendicular line, the smallest space walled off by this second set of lines is a hexagon.
In fact, this last construction works in generality: picking a point x, one then considers the geodesics between x and gx for g in Γ. Bisecting these geodesics is another set of curves, the locus
of points equidistant between x and gx. The smallest region enclosed by this second set of lines is the metric fundamental polygon.
where n is the genus of the Riemann surface (equivalently, where 4n is the number of the sides of the polygon). Since the standard polygon is a representative of H/Γ, the total area of the Riemann surface is equal to the area of the standard polygon. The area formula follows from the Gauss-Bonnet theorem and is in a certain sense generalized through the Riemann-Hurwitz formula
.
associated with the standard polygon. For a genus 
oriented surface, the group may be given by 
generators 
. These generators are given by the following fractional linear transforms acting on the upper half-plane:
for
. The parameters are given by
and
and
It may be verified that these generators obey the constraint
which gives the totality of the group presentation.
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, each closed surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
in the sense of geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
can be constructed from an even-sided oriented polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, called a fundamental polygon, by pairwise identification of its edges.
Examples
 Sphere |
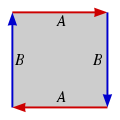 Real projective plane |
 Klein bottle |
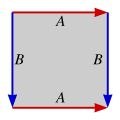 Torus |
- SphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
:
or 
- Real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
:
or 
- Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
:
or 
- TorusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
:
or 
Group generators
For the set of standard, symmetrical shapes, the symbols of the edges of the polygon may be understood to be the generators of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Then, the polygon, written in terms of group elements, becomes a constraint on the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
generated by the edges, giving a group presentation with one constraint.
Thus, for example, given the Euclidean plane
, let the group element act on the plane as while . Then generate the latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, and the torus is given by the quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
(a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
)
. More generally, the two generators can be taken to generate a parallelogram tiling, of fundamental parallelograms.For the torus, the constraint on the free group in two letters is given by
. This constraint is trivially embodied in the action on the plane given above. Alternately, the plane can be tiled by hexagons, and the centers of the hexagons form a hexagonal lattice. Identifying opposite edges of the hexagon again leads to the torus, this time, with the constraint describing the action of the hexagonal latticeHexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
generators on the plane.
In practice, most of the interesting cases are surfaces with negative curvature, and are thus realized by a discrete lattice
in the group acting on the upper half-plane. Such lattices are known as Fuchsian groupFuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s.
Standard fundamental polygons
An orientable closed surface of genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
n has the following standard fundamental polygon:
This fundamental polygon can be viewed as the result of glueing n tori together, and hence the surface is sometimes called the n-fold torus. ("Glueing" two surfaces means cutting a disk out of each and identifying the circular boundaries of the resulting holes.)
A non-orientable closed surface of (non-orientable) genus n has the following standard fundamental polygon:
Alternately, the non-orientable surfaces can be given in one of two forms, as n Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
s glued together (this may be called the n-fold Klein bottle, with non-orientable genus 2n), or as n glued real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
s (the n-fold crosscap, with non-orientable genus n). The n-fold Klein bottle is given by the 4n-sided polygon
(note the final
is missing the superscript −1; this flip, as compared to the orientable case, being the source of the non-orientability). The 2n+1-fold crosscap is given by the 4n+2-sided polygonThat these two cases exhaust all the possibilities for a compact non-orientable surface was shown by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
.
Fundamental polygon of a compact Riemann surface
The fundamental polygon of a (hyperbolic) compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
has a number of important properties that relate the surface to its Fuchsian model
Fuchsian model
In mathematics, a Fuchsian model is a construction of a hyperbolic Riemann surface R as a quotient of the upper half-plane H. By the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Every hyperbolic Riemann surface has a non-trivial fundamental group \pi_1...
. That is, a hyperbolic compact Riemann surface has the upper half-plane as the universal cover, and can be represented as a quotient manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
H/Γ where Γ is a non-Abelian group isomorphic to the deck transformation group of the surface. The cosets of the quotient space have the standard fundamental polygon as a representative element. In the following, note that all Riemann surfaces are orientable.
Metric fundamental polygon
Given a point in the upper half-plane H, and a discrete subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
Γ of PSL(2,R) that acts freely discontinuously
Free regular set
In mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X...
on the upper half-plane, then one can define the metric fundamental polygon as the set of points
Here, d is a hyperbolic metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
on the upper half-plane. The metric fundamental polygon is more usually called the Dirichlet region or the Voronoi polygon.
- This fundamental polygon is a fundamental domainFundamental domainIn geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
. - This fundamental polygon is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in that the geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
joining any two points of the polygon is contained entirely inside the polygon. - The diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of F is less than or equal to the diameter of H/Γ. In particular, the closure of F is compact. - If Γ has no fixed points in H and H/Γ is compact, then F will have finitely many sides.
- Each side of the polygon is a geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
arc. - For every side s of the polygon, there is precisely one other side s' such that gs=s' for some g in Γ. Thus, this polygon will have an even number of sides.
- The set of group elements g that join sides to each other are generatorsGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of Γ, and there is no smaller set that will generate Γ. - The upper half-plane is tiled by the closure of F under the action of Γ. That is,
where 
is the closure of F.
Standard fundamental polygon
Given any metric fundamental polygon F, one can construct, with a finite number of steps, another fundamental polygon, the standard fundamental polygon, which has an additional set of noteworthy properties:- The vertices of the standard polygon are all equivalent. By vertex is meant the point where two sides meet. By equivalent, it is meant that each vertex can be carried to any of the other vertices by some g in Γ.
- The number of sides is divisible by four.
- A given element g of Γ will carry at most one side of the polygon to another. Thus, the sides can be marked off in pairs. Since the action of Γ is orientation-preserving, if one side is called
, then the other of the pair can be marked with the opposite orientation 
. - The edges of the standard polygon can be arranged so that the list of adjacent sides takes the form
. That is, pairs of sides can be arranged so that they interleave in this way. - The standard polygon is convex.
- The sides can be arranged to be geodesic arcs.
The above construction is sufficient to guarantee that each side of the polygon is a closed (non-trivial) loop in the manifold H/Γ. As such, each side can thus an element of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
. In particular, the fundamental group has 2n generators , with exactly one defining constraint,.The genus of the resulting manifold H/Γ is n.
Example
The metric fundamental polygon and the standard fundamental polygon will usually have a different number of sides. Thus, for example, the standard fundamental polygon on a torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
is a fundamental parallelogram. By contrast, the metric fundamental polygon is six-sided, a hexagon. This can be most easily seen by noting that the sides of the hexagon are perpendicular bisectors of the edges of the parallelogram. That is, one picks a point in the lattice, and then considers the set of straight lines joining this point to nearby neighbors. Bisecting each such line by another perpendicular line, the smallest space walled off by this second set of lines is a hexagon.
In fact, this last construction works in generality: picking a point x, one then considers the geodesics between x and gx for g in Γ. Bisecting these geodesics is another set of curves, the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points equidistant between x and gx. The smallest region enclosed by this second set of lines is the metric fundamental polygon.
Area
The area of the standard fundamental polygon is where n is the genus of the Riemann surface (equivalently, where 4n is the number of the sides of the polygon). Since the standard polygon is a representative of H/Γ, the total area of the Riemann surface is equal to the area of the standard polygon. The area formula follows from the Gauss-Bonnet theorem and is in a certain sense generalized through the Riemann-Hurwitz formulaRiemann-Hurwitz formula
In mathematics, the Riemann–Hurwitz formula, named after Bernhard Riemann and Adolf Hurwitz, describes the relationship of the Euler characteristics of two surfaces when one is a ramified covering of the other. It therefore connects ramification with algebraic topology, in this case...
.
Explicit form for standard polygons
Explicit expressions can be given for the standard polygons. One of the more useful forms is in terms of the group associated with the standard polygon. For a genus oriented surface, the group may be given by generators . These generators are given by the following fractional linear transforms acting on the upper half-plane:for
. The parameters are given byand
and
It may be verified that these generators obey the constraint
which gives the totality of the group presentation.
Generalizations
In higher dimensions, the idea of the fundamental polygon is captured in the articulation of homogeneous spaceHomogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
s.