
Tetrahemihexahedron
Encyclopedia
In geometry
, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure
is a crossed quadrilateral
. It has Coxeter-Dynkin diagram
of .
It is the only non-prismatic uniform polyhedron
with an odd number of faces.
It is a hemipolyhedron
. The "hemi" part of the name means some of the faces form a group with half as many members as some regular polyhedron—here, three square faces form a group with half as many faces as the regular hexahedron, better known as the cube—hence hemihexahedron. Hemi faces are also oriented in the same direction as the regular polyhedron's faces. The three square faces of the tetrahemihexahedron are, like the three facial orientations of the cube, mutually perpendicular
.
The "half-as-many" characteristic also means that hemi faces must pass through the center of the polyhedron, where they all intersect each other. Visually, each square is divided into four right triangle
s, with two visible from each side.
. It also shares 4 of the 8 triangular faces of the octahedron, but has three additional square faces passing through the centre of the polyhedron.
The dual figure is the tetrahemihexacron
.
It is 2-covered by the cuboctahedron
, which accordingly has the same abstract
vertex figure
(2 triangles and two squares: 3.4.3.4) and twice the vertices, edges, and faces.
surface. It is unique as the only uniform polyhedron
with an Euler characteristic
of 1 and is hence a projective polyhedron
, yielding a representation of the real projective plane
very similar to the Roman surface
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a crossed quadrilateral
Antiparallelogram
An antiparallelogram is a quadrilateral in which, like a parallelogram, the pairs of nonadjacent sides are congruent, but in which two opposite sides intersect and are therefore not parallel.-Properties:Every antiparallelogram has an axis of symmetry through its crossing point...
. It has Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
of .
It is the only non-prismatic uniform polyhedron
Prismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...
with an odd number of faces.
It is a hemipolyhedron
Hemipolyhedron
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron - hence the "hemi" prefix.The prefix "hemi"...
. The "hemi" part of the name means some of the faces form a group with half as many members as some regular polyhedron—here, three square faces form a group with half as many faces as the regular hexahedron, better known as the cube—hence hemihexahedron. Hemi faces are also oriented in the same direction as the regular polyhedron's faces. The three square faces of the tetrahemihexahedron are, like the three facial orientations of the cube, mutually perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
.
The "half-as-many" characteristic also means that hemi faces must pass through the center of the polyhedron, where they all intersect each other. Visually, each square is divided into four right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s, with two visible from each side.
Related polyhedra
It has the same vertices and edges as the regular octahedronOctahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. It also shares 4 of the 8 triangular faces of the octahedron, but has three additional square faces passing through the centre of the polyhedron.
 Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 Tetrahemihexahedron |
The dual figure is the tetrahemihexacron
Tetrahemihexacron
In geometry, the tetrahemihexacron is the dual of the tetrahemihexahedron, and is one of nine dual hemipolyhedra.Since the tetrahemihexahedron has three square faces passing through the model centre, the tetrahemihexacron has three vertices at infinity...
.
It is 2-covered by the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
, which accordingly has the same abstract
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
(2 triangles and two squares: 3.4.3.4) and twice the vertices, edges, and faces.
 Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 Tetrahemihexahedron |
Related surfaces
It is a non-orientableOrientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
surface. It is unique as the only uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
with an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of 1 and is hence a projective polyhedron
Projective polyhedron
In geometry, a projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids....
, yielding a representation of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
very similar to the Roman surface
Roman surface
The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
.
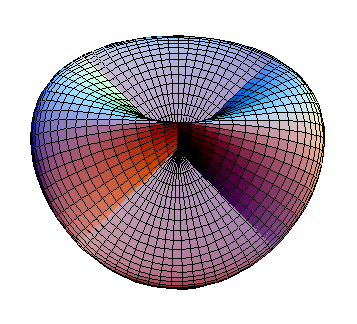 Roman surface Roman surface The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry... |

