Phonon
Encyclopedia
.gif)
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s. Often referred to as a quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
, it represents an excited state in the quantum mechanical quantization of the modes of vibrations of elastic structures of interacting particles.
Phonons play a major role in many of the physical properties of solids, including a material's thermal
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
and electrical conductivities. Hence the study of phonons is an important part of solid state physics.
A phonon is a quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
description of a special type of vibration
Vibration
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic such as the motion of a pendulum or random such as the movement of a tire on a gravel road.Vibration is occasionally "desirable"...
al motion, in which a lattice uniformly oscillates at the same frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
. In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
this is known as the normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
. The normal mode is important because any arbitrary lattice vibration can be considered as a superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of these elementary vibrations (cf. Fourier analysis). While normal modes are wave-like
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
phenomena in classical mechanics, they have particle-like
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
properties in the wave–particle duality
Wave–particle duality
Wave–particle duality postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale objects...
of quantum mechanics.
The name phonon comes from the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
word φωνή (phonē), which translates as sound or voice because long-wavelength phonons give rise to sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
.
The concept of phonons was introduced in 1932 by Russian physicist Igor Tamm
Igor Tamm
Igor Yevgenyevich Tamm was a Soviet physicist and Nobel laureate who received most prestigious Nobel Prize in Physics, jointly with Pavel Alekseyevich Cherenkov and Ilya Frank, for the discovery of Cherenkov radiation, made in 1934.-Biography:Tamm was born in Vladivostok, Russian Empire , in a...
.
Lattice dynamics
The equations in this section either do not use axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of quantum mechanics or use relations for which there exists a direct correspondence
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
in classical mechanics.
For example, consider a rigid regular, crystalline, i.e. not amorphous, lattice composed of N particles. We will refer to these particles as atoms, although in a real solid these may be molecules. N is some large number, say around 1023 (on the order of Avogadro's number
Avogadro's number
In chemistry and physics, the Avogadro constant is defined as the ratio of the number of constituent particles N in a sample to the amount of substance n through the relationship NA = N/n. Thus, it is the proportionality factor that relates the molar mass of an entity, i.e...
) for a typical sample of solid. If the lattice is rigid, the atoms must be exerting force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s on one another to keep each atom near its equilibrium position. These forces may be Van der Waals force
Van der Waals force
In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
s, covalent bond
Covalent bond
A covalent bond is a form of chemical bonding that is characterized by the sharing of pairs of electrons between atoms. The stable balance of attractive and repulsive forces between atoms when they share electrons is known as covalent bonding....
s, electrostatic attractions, and others, all of which are ultimately due to the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
force. Magnetic
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
and gravitational forces are generally negligible. The forces between each pair of atoms may be characterized by a potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
function V that depends on the distance of separation of the atoms. The potential energy of the entire lattice is the sum of all pairwise potential energies:
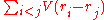
where
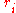 is the position
is the positionSpace
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
of the
 th atom, and
th atom, and  is the potential energy
is the potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
between two atoms.
It is difficult to solve this many-body problem
Many-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
in full generality, in either classical or quantum mechanics. In order to simplify the task, we introduce two important approximations. First, we perform the sum over neighboring atoms only. Although the electric forces in real solids extend to infinity, this approximation is nevertheless valid because the fields produced by distant atoms are screened
Electric field screening
Screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases and conduction electrons in semiconductors and metals....
. Secondly, we treat the potentials
 as harmonic potentials
as harmonic potentialsHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
: this is permissible as long as the atoms remain close to their equilibrium positions. (Formally, this is done by Taylor expanding
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
 about its equilibrium value to quadratic order, giving
about its equilibrium value to quadratic order, giving  proportional to the displacement
proportional to the displacement 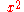 and the elastic force simply proportional to
and the elastic force simply proportional to  . The error in ignoring higher order terms remains small if
. The error in ignoring higher order terms remains small if  remains close to the equilibrium position).
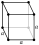
remains close to the equilibrium position).The resulting lattice may be visualized as a system of balls connected by springs. The following figure shows a cubic lattice, which is a good model for many types of crystalline solid. Other lattices include a linear chain, which is a very simple lattice which we will shortly use for modelling phonons. Other common lattices may be found in the article on crystal structure
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
.
The potential energy of the lattice may now be written as

Here,
 is the natural frequency of the harmonic potentials, which we assume to be the same since the lattice is regular.
is the natural frequency of the harmonic potentials, which we assume to be the same since the lattice is regular. 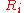 is the position coordinate of the
is the position coordinate of the  th atom, which we now measure from its equilibrium position. The sum over nearest neighbors is denoted as "(nn)".
th atom, which we now measure from its equilibrium position. The sum over nearest neighbors is denoted as "(nn)".Lattice waves
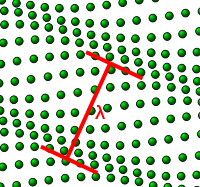
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s propagating through the lattice. One such wave is shown in the figure to the right. The amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the wave is given by the displacements of the atoms from their equilibrium positions. The wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
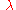 is marked.
is marked.There is a minimum possible wavelength, given by twice the equilibrium separation a between atoms. As we shall see in the following sections, any wavelength shorter than this can be mapped onto a wavelength longer than 2a, due to the periodicity of the lattice.
Not every possible lattice vibration has a well-defined wavelength and frequency. However, the normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
s do possess well-defined wavelengths and frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
.
One dimensional lattice
In order to simplify the analysis needed for a 3-dimensional lattice of atoms it is convenient to model a 1-dimensional lattice or linear chain. This model is complex enough to display the salient features of phonons.Classical treatment
The forces between the atoms are assumed to be linear and nearest-neighbour,and they are represented by an elastic spring. Each atom is assumed to be a point particle and the nucleus and electrons move in step.(adiabatic approximation)
-
-
-
-
-
-
-
- n-1 n n+1 ← d →
-
-
-
-
-
-
 o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o
o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o
-
-
-
-
-
-
-
-
- →→→→→→
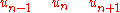
-
-
-
-
-
-
-
Where
 labels the n'th atom,
labels the n'th atom, 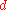 is the distance between atoms when the chain is in equilibrium and
is the distance between atoms when the chain is in equilibrium and 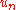 the displacement of the n'th atom from its equilibrium position.
the displacement of the n'th atom from its equilibrium position.If C is the elastic constant of the spring and m the mass of the atom then the equation of motion of the n'th atom is :
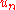
This is a set of coupled equations and since we expect the solutions to be oscillatory, new coordinates can be defined by a discrete Fourier transform, in order to de-couple them.
Put
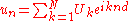
Here
 replaces the usual continuous variable
replaces the usual continuous variable  . The
. The 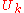 are known as the normal coordinates. Substitution into the equation of motion produces the following decoupled equations.(This requires a significant manipulation using the orthonormality and completeness relations of the discrete fourier transform )
are known as the normal coordinates. Substitution into the equation of motion produces the following decoupled equations.(This requires a significant manipulation using the orthonormality and completeness relations of the discrete fourier transform )These are the equations for harmonic oscillators which have the solution:
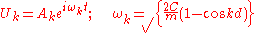
Each normal coordinate
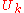 represents an independent vibrational mode of the lattice with wavenumber
represents an independent vibrational mode of the lattice with wavenumber 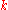 which is known as a normal mode
which is known as a normal modeNormal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
. The second equation for
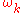 is known as the dispersion relation
is known as the dispersion relationDispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
between the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
and the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
.
Quantum treatment
Consider a one-dimensional quantum mechanical harmonic chain of N identical atoms. This is the simplest quantum mechanical model of a lattice, and we will see how phonons arise from it. The formalism that we will develop for this model is readily generalizable to two and three dimensions. The HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
for this system is

where
 is the mass of each atom, and
is the mass of each atom, and 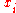 and
and 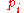 are the position and momentum
are the position and momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
operators for the
 th atom. A discussion of similar Hamiltonians may be found in the article on the quantum harmonic oscillator
th atom. A discussion of similar Hamiltonians may be found in the article on the quantum harmonic oscillatorQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
.
We introduce a set of
 "normal coordinates"
"normal coordinates"  , defined as the discrete Fourier transform
, defined as the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
s of the
 's and
's and  "conjugate momenta"
"conjugate momenta" 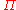 defined as the Fourier transforms of the
defined as the Fourier transforms of the 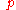 's:
's: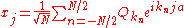
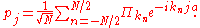
The quantity
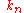 will turn out to be the wave number
will turn out to be the wave numberWavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
of the phonon, i.e.
 divided by the wavelength
divided by the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. It takes on quantized values, because the number of atoms is finite. The form of the quantization depends on the choice of boundary conditions; for simplicity, we impose periodic boundary conditions, defining the
 th atom as equivalent to the first atom. Physically, this corresponds to joining the chain at its ends. The resulting quantization is
th atom as equivalent to the first atom. Physically, this corresponds to joining the chain at its ends. The resulting quantization is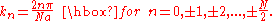
The upper bound to
 comes from the minimum wavelength, which is twice the lattice spacing
comes from the minimum wavelength, which is twice the lattice spacing  , as discussed above.
, as discussed above.By inverting the discrete Fourier transforms to express the
 's in terms of the
's in terms of the  's and the
's and the 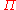 's in terms of the
's in terms of the 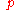 's, and using the canonical commutation relations between the
's, and using the canonical commutation relations between the  's and
's and 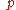 's, we can show that
's, we can show that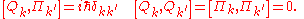
In other words, the normal coordinates and their conjugate momenta obey the same commutation relations as position and momentum operators! Writing the Hamiltonian in terms of these quantities,
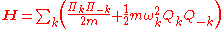
where
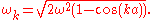
Notice that the couplings between the position variables have been transformed away; if the
 's and
's and 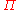 's were Hermitian
's were HermitianHermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
(which they are not), the transformed Hamiltonian would describe
 uncoupled harmonic oscillators.
uncoupled harmonic oscillators.The harmonic oscillator eigenvalues or energy levels for the mode
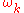 are :
are :If we ignore the zero-point energy then the levels are evenly spaced at :
So a minimum amount of energy
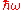 must be supplied to the harmonic oscillator(or normal mode) to move it to the next energy level. In comparison to the photon case when the electromagnetic field is quantised, the quantum of vibrational energy is called a phonon.
must be supplied to the harmonic oscillator(or normal mode) to move it to the next energy level. In comparison to the photon case when the electromagnetic field is quantised, the quantum of vibrational energy is called a phonon.All quantum systems show wave-like and particle-like properties. The particle-like properties of the phonon are best understood using the methods of second-quantisation and operator techniques described later.
Three dimensional lattice
This may be generalized to a three-dimensional lattice. The wave number k is replaced by a three-dimensional wave vectorWave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
k. Furthermore, each k is now associated with three normal coordinates.
The new indices s = 1, 2, 3 label the polarization of the phonons. In the one dimensional model, the atoms were restricted to moving along the line, so the phonons corresponded to longitudinal wave
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
s. In three dimensions, vibration is not restricted to the direction of propagation, and can also occur in the perpendicular planes, like transverse wave
Transverse wave
A transverse wave is a moving wave that consists of oscillations occurring perpendicular to the direction of energy transfer...
s. This gives rise to the additional normal coordinates, which, as the form of the Hamiltonian indicates, we may view as independent species of phonons.
Dispersion relation
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of a phonon,
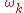 , to its wave number
, to its wave number 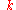 :
: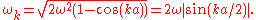
This is known as a dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
.
The speed of propagation of a phonon, which is also the speed of sound
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
in the lattice, is given by the slope of the dispersion relation,
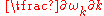 (see group velocity
(see group velocityGroup velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
.) At low values of
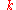 (i.e. long wavelengths), the dispersion relation is almost linear, and the speed of sound is approximately
(i.e. long wavelengths), the dispersion relation is almost linear, and the speed of sound is approximately  , independent of the phonon frequency. As a result, packets of phonons with different (but long) wavelengths can propagate for large distances across the lattice without breaking apart. This is the reason that sound propagates through solids without significant distortion. This behavior fails at large values of
, independent of the phonon frequency. As a result, packets of phonons with different (but long) wavelengths can propagate for large distances across the lattice without breaking apart. This is the reason that sound propagates through solids without significant distortion. This behavior fails at large values of 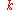 , i.e. short wavelengths, due to the microscopic details of the lattice.
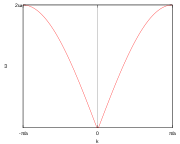
, i.e. short wavelengths, due to the microscopic details of the lattice.For a crystal that has at least two atoms in its primitive cell (which may or may not be different), the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
s exhibit two types of phonons, namely, optical and acoustic modes corresponding to the upper and lower sets of curves in the diagram, respectively. The vertical axis is the energy or frequency of phonon, while the horizontal axis is the wave-vector. The boundaries at -km and km are those of the first Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. The blue, violet, and brown curves are those of longitudinal
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
acoustic, transverse
Transverse wave
A transverse wave is a moving wave that consists of oscillations occurring perpendicular to the direction of energy transfer...
acoustic 1, and transverse
Transverse wave
A transverse wave is a moving wave that consists of oscillations occurring perpendicular to the direction of energy transfer...
acoustic 2 modes, respectively.
In some crystals the two transverse acoustic modes have exactly the same dispersion curve. It is also interesting that for a crystal with N ( > 2) different atoms in a primitive cell
Primitive cell
Used predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
, there are always three acoustic modes. The number of optical modes is 3N - 3. Many phonon dispersion curves have been measured by neutron scattering
Neutron scattering
Neutron scattering,the scattering of free neutrons by matter,is a physical processand an experimental technique using this processfor the investigation of materials.Neutron scattering as a physical process is of primordial importance...
.
The physics of sound in fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s differs from the physics of sound in solids, although both are density waves: sound waves in fluids only have longitudinal components, whereas sound waves in solids have longitudinal and transverse components. This is because fluids can't support shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
es. (but see viscoelastic fluids, which only apply to high frequencies, though).
Interpretation of phonons using second quantisation techniques
In fact, the above-derived Hamiltonian looks like the classical Hamiltonian function, but if it is interpreted as an operatorOperator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
, then it describes a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of non-interacting boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s.
This leads to new physics.
The energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
spectrum of this Hamiltonian is easily obtained by the method of ladder operators, similar to the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
problem. We introduce a set of ladder operators defined by
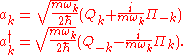
The ladder operators satisfy the following identities:
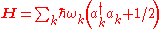
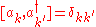
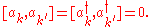
As with the quantum harmonic oscillator, we can then show that
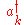 and
and 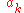 respectively create and destroy one excitation of energy
respectively create and destroy one excitation of energy  . These excitations are phonons.
. These excitations are phonons.We can immediately deduce two important properties of phonons. Firstly, phonons are boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, since any number of identical excitations can be created by repeated application of the creation operator
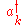 . Secondly, each phonon is a "collective mode" caused by the motion of every atom in the lattice. This may be seen from the fact that the ladder operators contain sums over the position and momentum operators of every atom.
. Secondly, each phonon is a "collective mode" caused by the motion of every atom in the lattice. This may be seen from the fact that the ladder operators contain sums over the position and momentum operators of every atom.It is not a priori obvious that these excitations generated by the
 operators are literally waves of lattice displacement, but one may convince oneself of this by calculating the position-position correlation function
operators are literally waves of lattice displacement, but one may convince oneself of this by calculating the position-position correlation functionCorrelation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
. Let
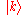 denote a state with a single quantum of mode
denote a state with a single quantum of mode 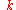 excited, i.e.
excited, i.e.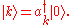
One can show that, for any two atoms
 and
and  ,
,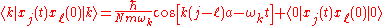
which is exactly what we would expect for a lattice wave with frequency
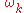 and wave number
and wave number 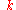 .
.In three dimensions the Hamiltonian has the form
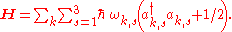
Acoustic and optical phonons
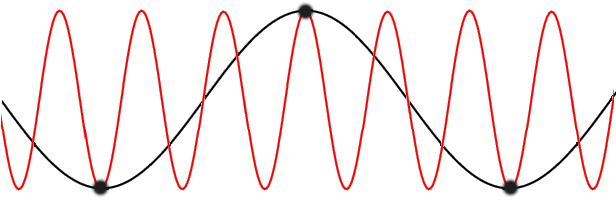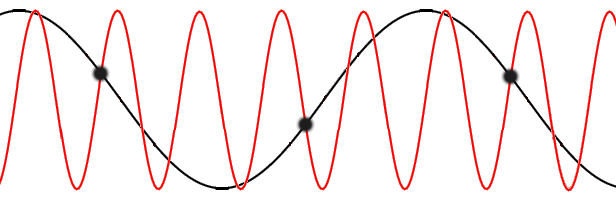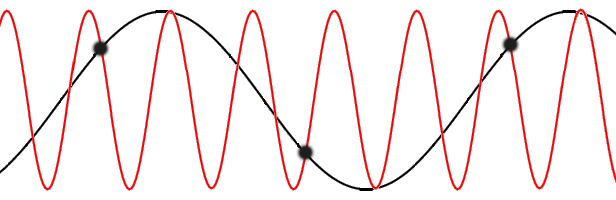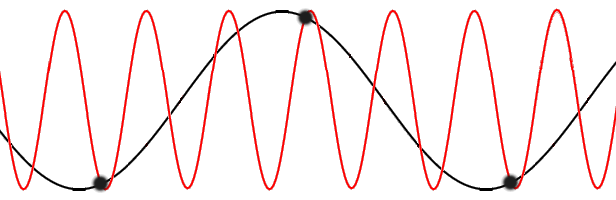
Solids with more than one type of atom - either with different masses or bonding strengths - in the smallest unit cell, exhibit two types of phonons: acoustic phonons and optical phonons.Acoustic phonons are coherent movements of atoms of the lattice out of their equilibrium positions. The displacement as a function of position can be given by a cos(wx). If the displacement is in the direction of propagation, then in some areas the atoms will be closer, in others further apart, as in a sound wave in air (hence the name acoustic). Displacement perpendicular to the propagation direction is comparable to waves in water. If the wavelength of acoustic phonons goes to infinity, this corresponds to a simple displacement of the whole crystal, and this costs zero energy. Acoustic phonons exhibit a linear relationship between frequency and phonon wavevector for long wavelengths. The frequencies of acoustic phonons tend to zero with longer wavelength. Longitudinal and transverse acoustic phonons are often abbreviated as LA and TA phonons, respectively.
Optical phonons are out of phase movement of the atoms in the lattice, one atom moving to the left, and it's neighbour to the right. This occurs if the lattice is made of atoms of different charge or mass. They are called optical because in ionic crystals, such as sodium chloride
Sodium chloride
Sodium chloride, also known as salt, common salt, table salt or halite, is an inorganic compound with the formula NaCl. Sodium chloride is the salt most responsible for the salinity of the ocean and of the extracellular fluid of many multicellular organisms...
, they are excited by infrared radiation. The electric field of the light will move every positive sodium ion in the direction of the field, and every negative chloride ion in the other direction, sending the crystal vibrating.
Optical phonons have a non-zero frequency at the Brillouin zone center and show no dispersion near that long wavelength limit. This is because they correspond to a mode of vibration where positive and negative ions at adjacent lattice sites swing against each other, creating a time-varying electrical dipole moment. Optical phonons that interact in this way with light are called infrared active. Optical phonons that are Raman active can also interact indirectly with light, through Raman scattering
Raman scattering
Raman scattering or the Raman effect is the inelastic scattering of a photon. It was discovered by Sir Chandrasekhara Venkata Raman and Kariamanickam Srinivasa Krishnan in liquids, and by Grigory Landsberg and Leonid Mandelstam in crystals....
. Optical phonons are often abbreviated as LO and TO phonons, for the longitudinal and transverse modes respectively.
When measuring optical phonon energy by experiment, optical phonon frequencies,
 , are often given in units of cm
, are often given in units of cmCM
- Places :* Cameroon, which has the ISO and FIPS country code "CM"** .cm, the country code top-level domain for Cameroon* Chelmsford, which has the British post code "CM"- Science :* Centimetre a unit of length equal to one hundredth of a metre...
 , which are the same units as the wavevector. This value corresponds to the inverse of the wavelength
, which are the same units as the wavevector. This value corresponds to the inverse of the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
with the same energy as the measured phonon. The cm
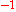 is a unit of energy used frequently in the dispersion relations of both acoustic and optical phonons, see units of energy for more details and uses.
is a unit of energy used frequently in the dispersion relations of both acoustic and optical phonons, see units of energy for more details and uses.Crystal momentum
 as though it has a momentum
as though it has a momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
 , by analogy to photon
, by analogy to photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s and matter waves. This is not entirely correct, for
 is not actually a physical momentum; it is called the crystal momentum or pseudomomentum. This is because
is not actually a physical momentum; it is called the crystal momentum or pseudomomentum. This is because  is only determined up to multiples of constant vectors, known as reciprocal lattice vector
is only determined up to multiples of constant vectors, known as reciprocal lattice vectorReciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
s. For example, in our one-dimensional model, the normal coordinates
 and
and 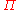 are defined so that
are defined so that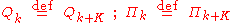
where
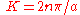
for any integer
 . A phonon with wave number
. A phonon with wave number 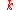 is thus equivalent to an infinite "family" of phonons with wave numbers
is thus equivalent to an infinite "family" of phonons with wave numbers  ,
,  , and so forth. Physically, the reciprocal lattice vectors act as additional "chunks" of momentum which the lattice can impart to the phonon. Bloch electron
, and so forth. Physically, the reciprocal lattice vectors act as additional "chunks" of momentum which the lattice can impart to the phonon. Bloch electronBloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
s obey a similar set of restrictions.
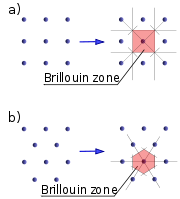
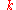 which have the smallest magnitude
which have the smallest magnitude 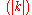 in their "family". The set of all such wave vectors defines the first Brillouin zone
in their "family". The set of all such wave vectors defines the first Brillouin zoneBrillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. Additional Brillouin zones may be defined as copies of the first zone, shifted by some reciprocal lattice vector.
It is interesting that similar consideration is needed in analog-to-digital conversion
Analog-to-digital converter
An analog-to-digital converter is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement...
where aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
may occur under certain conditions.
Thermodynamics
The thermodynamicThermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
properties of a solid are directly related to its phonon structure. The entire set of all possible phonons that are described by the above phonon dispersion relations combine in what is known as the phonon density of states
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
which determines the heat capacity of a crystal.
At absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
temperature, a crystal lattice lies in its ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
, and contains no phonons. A lattice at a non-zero temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
has an energy that is not constant, but fluctuates randomly about some mean value
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
. These energy fluctuations are caused by random lattice vibrations, which can be viewed as a gas of phonons. (The random motion of the atoms in the lattice is what we usually think of as heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
.) Because these phonons are generated by the temperature of the lattice, they are sometimes referred to as thermal phonons.
Unlike the atoms which make up an ordinary gas, thermal phonons can be created and destroyed by random energy fluctuations. In the language of statistical mechanics this means that the chemical potential for adding a phonon is zero. This behavior is an extension of the harmonic potential, mentioned earlier, into the anharmonic regime. The behavior of thermal phonons is similar to the photon gas produced by an electromagnetic cavity
Electromagnetic cavity
An electromagnetic cavity is a cavity that acts as a container for electromagnetic fields such as photons, in effect containing their wave function inside. The size of the cavity determines the maximum photon wave length that can be trapped. Additionally, it produces quantized energy levels for...
, wherein photons may be emitted or absorbed by the cavity walls. This similarity is not coincidental, for it turns out that the electromagnetic field behaves like a set of harmonic oscillators; see Black-body radiation
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
. Both gases obey the Bose-Einstein statistics: in thermal equilibrium and within the harmonic regime, the probability of finding phonons (or photons) in a given state with a given angular frequency is:

where
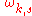 is the frequency of the phonons (or photons) in the state,
is the frequency of the phonons (or photons) in the state, 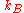 is Boltzmann's constant, and
is Boltzmann's constant, and 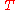 is the temperature.
is the temperature.Operator formalism
The phonon Hamiltonian is given by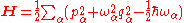
In terms of the operators, these are given by
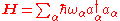
Here, in expressing the Hamiltonian (quantum mechanics)
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
in operator formalism, we have not taken into account the
 term, since if we take an infinite lattice or, for that matter a continuum, the
term, since if we take an infinite lattice or, for that matter a continuum, the  terms will add up giving an infinity. Hence, it is "renormalized" by putting the factor of
terms will add up giving an infinity. Hence, it is "renormalized" by putting the factor of  to 0 arguing that the difference in energy is what we measure and not the absolute value of it. Hence, the
to 0 arguing that the difference in energy is what we measure and not the absolute value of it. Hence, the  factor is absent in the operator formalised expression for the Hamiltonian
factor is absent in the operator formalised expression for the HamiltonianHamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
.
The ground state also called the "vacuum state" is the state composed of no phonons. Hence, the energy of the ground state is 0. When, a system is in state
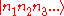 , we say there are
, we say there are 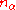 phonons of type
phonons of type  . The
. The 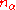 are called the occupation number of the phonons. Energy of a single phonon of type
are called the occupation number of the phonons. Energy of a single phonon of type  being
being  , the total energy of a general phonon system is given by
, the total energy of a general phonon system is given by 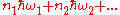 . In other words, the phonons are non-interacting. The action of creation and annihilation operators are given by
. In other words, the phonons are non-interacting. The action of creation and annihilation operators are given by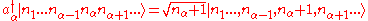
and,
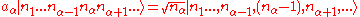
i.e.
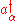 creates a phonon of type
creates a phonon of type  while
while 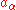 annihilates. Hence, they are respectively the creation and annihilation operator for phonons. Analogous to the Quantum harmonic oscillator
annihilates. Hence, they are respectively the creation and annihilation operator for phonons. Analogous to the Quantum harmonic oscillatorQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
case, we can define particle number operator
Particle number operator
In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles.The number operator acts on Fock space...
as
 . The number operator commutes with a string of products of the creation and annihilation operators if, the number of
. The number operator commutes with a string of products of the creation and annihilation operators if, the number of  's are equal to number of
's are equal to number of 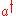 's.
's.Phonons are bosons since,
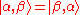 i.e. they are symmetric under exchange.
i.e. they are symmetric under exchange.See also
- BosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
- FractonFractonA fracton is a collective quantized vibration on a substrate with a fractal structure.Fractons are the fractal analog of phonons. Phonons are the result of applying translational symmetry to the potential in a Schrödinger equation. Fractal self-similarity can be thought of as a symmetry somewhat...
- Rayleigh waveRayleigh waveRayleigh waves are a type of surface acoustic wave that travels on solids. They are produced on the Earth by earthquakes, in which case they are also known as "ground roll", or by other sources of seismic energy such as ocean waves an explosion or even a sledgehammer impact...
- Brillouin scatteringBrillouin scatteringBrillouin scattering, named after Léon Brillouin, occurs when light in a medium interacts with time dependent optical density variations and changes its energy and path. The density variations may be due to acoustic modes, such as phonons, magnetic modes, such as magnons, or temperature gradients...
- Linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
- Phononic crystal
- Relativistic heat conductionRelativistic heat conductionThe theory of relativistic heat conduction claims to be the only model for heat conduction that is compatible with the theory of special relativity, the second law of thermodynamics, electrodynamics, and quantum mechanics, simultaneously...
- Surface acoustic waveSurface acoustic wave]A surface acoustic wave is an acoustic wave traveling along the surface of a material exhibiting elasticity, with an amplitude that typically decays exponentially with depth into the substrate.-Discovery:...
- Second soundSecond soundSecond sound is a quantum mechanical phenomenon in which heat transfer occurs by wave-like motion, rather than by the more usual mechanism of diffusion. Heat takes the place of pressure in normal sound waves. This leads to a very high thermal conductivity...
- Rigid Unit ModesRigid Unit ModesRigid unit modes represent a class of lattice vibrations or phonons that exist in network materials such as quartz, cristobalite or zirconium tungstate. Network materials can be described as three-dimensional networks of polyhedral groups of atoms such as SiO4 tetrahedra or TiO6 octahedra...
- Surface phononSurface phononPhonons are collective lattice vibration modes, and surface phonons are those particular modes associated with surfaces; they are an artifact of periodicity, symmetry, and the termination of bulk crystal structure associated with the surface layer of a solid [1]...
- SASERSaserSaser may refer to:* a nickname for one of the best schools in Malaysia, Sekolah Menengah Sains Seremban* the Saser Muztagh range of the Karakoram* Sasser Pass , on the old caravan route between Ladakh and Yarkand...
- Thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
External links
- Optical and acoustic modes
- Phonons in a One Dimensional Microfluidic Crystal http://www.nature.com/nphys/journal/v2/n11/abs/nphys432.html and http://arxiv.org/abs/1008.1155 with movies in http://www.weizmann.ac.il/materials/barziv/project_1.htm.