
Four-force
Encyclopedia
In the special theory of relativity four-force is a four-vector
that replaces the classical force
; the four-force is the four-vector defined as the change in four-momentum
over the particle's own time
:
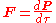 .
.
For a particle of constant invariant mass
m > 0,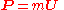 where
where 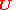 is the four-velocity
is the four-velocity
, so we can relate the four-force with the four-acceleration
as in Newton's second law:
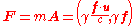 .
.
Here

and
 .
.
In general relativity
the relation between four-force, and four-acceleration
remains the same, but the elements of the four-force are related to the elements of the four-momentum
through a covariant derivative
with respect to proper time.

(4-force acting to charged particle situated in electromagnetic field) can be expressed as: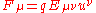 , where
, where 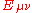 - electromagnetic tensor
- electromagnetic tensor
, - 4-velocity,
- 4-velocity, 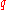 - electric charge
- electric charge
.
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
that replaces the classical force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
; the four-force is the four-vector defined as the change in four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
over the particle's own time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
:
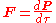 .
.For a particle of constant invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
m > 0,
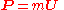 where
where 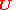 is the four-velocity
is the four-velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
, so we can relate the four-force with the four-acceleration
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
as in Newton's second law:
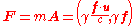 .
.Here

and
 .
.In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
the relation between four-force, and four-acceleration
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
remains the same, but the elements of the four-force are related to the elements of the four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
through a covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
with respect to proper time.

Examples
In special relativity, Lorentz 4-forceLorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
(4-force acting to charged particle situated in electromagnetic field) can be expressed as:
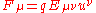 , where
, where 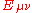 - electromagnetic tensor
- electromagnetic tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
,
 - 4-velocity,
- 4-velocity, 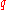 - electric charge
- electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
.

