Charge conservation
Encyclopedia
In physics
, charge conservation is the principle that electric charge
can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved
. The first written statement of the principle was by American scientist and statesman Benjamin Franklin
in 1747.
Charge conservation is a physical law that states that the change in the amount of electric charge in any volume of space is exactly equal to the amount of charge flowing into the volume minus the amount of charge flowing out of the volume. In essence, charge conservation is an accounting relationship between the amount of charge in a region and the flow of charge into and out of that region.
Mathematically, we can state the law as a continuity equation
:
Q(t) is the quantity of electric charge in a specific volume at time t, QIN is
the amount of charge flowing into the volume between time t1 and t2, and QOUT is the amount of charge flowing out of the volume during the same time period.
This does not mean that individual positive and negative charges cannot be created or destroyed. Electric charge is carried by subatomic particle
s such as electron
s and proton
s, which can be created and destroyed. In particle physics
, charge conservation means that in elementary particle reactions that create charged particles, equal numbers of positive and negative particles are always created, keeping the net amount of charge unchanged. Similarly, when particles are destroyed, equal numbers of positive and negative charges are destroyed.
Although conservation of charge requires that the total quantity of charge in the universe is constant, it leaves open the question of what that quantity is. Most evidence indicates that the total charge in the universe is zero; that is, there are equal quantities of positive and negative charge.
ρ (in coulombs per cubic meter) and electric current density
J (in amperes per square meter):
This statement is equivalent to a conservation of four-current
. In the mid-nineteenth century, James Clerk Maxwell
postulated the existence of electromagnetic waves as a result of his discovery that Ampère's law
(in its original form) was inconsistent with the conservation of charge. After correctly reformulating Ampère's law
, Maxwell also realized that such waves would travel at the speed of light
, and that light itself must be a form of electromagnetic radiation. See electromagnetic wave equation
for a full discussion of these discoveries.
where S = ∂V is the boundary of V oriented by outward-pointing normals
, and dS is shorthand for NdS, the outward pointing normal of the boundary ∂V. Here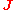
is the current density (charge per unit area per unit time) at the surface of the volume. The vector points in the direction of the current.
From the Divergence theorem
this can be written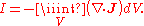
Charge conservation requires that the net current into a volume must necessarily equal the net change in charge within the volume.
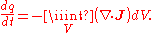
Charge is related to charge density by the relation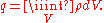
This yields
Since this is true for every volume, we have in general
, a central result in theoretical physics that asserts that each conservation law
is associated with a symmetry
of the underlying physics. The symmetry that is associated with charge conservation is the global gauge invariance of the electromagnetic field
. This is related to the fact that the electric and magnetic fields are not changed by different choices of the value representing the zero point of electrostatic potential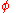
. However the full symmetry is more complicated, and also involves the vector potential
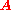. The full statement of gauge invariance is that the physics of an electromagnetic field are unchanged when the scalar and vector potential are shifted by the gradient of an arbitrary scalar field
:
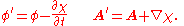
In quantum mechanics the scalar field is equivalent to a phase shift in the wavefunction
of the charged particle:
so gauge invariance is equivalent to the well known fact that changes in the phase of a wavefunction are unobservable, and only changes in the magnitude of the wavefunction result in changes to the probability function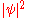
. This is the ultimate theoretical origin of charge conservation.
Gauge invariance is a very important, well established property of the electromagnetic field and has many testable consequences. The theoretical justification for charge conservation is greatly strengthened by being linked to this symmetry. For example, local gauge invariance also requires that the photon
be massless, so the good experimental evidence that the photon has zero mass is also strong evidence that charge is conserved.
Even if gauge symmetry is exact, however, there might be apparent electric charge non-conservation if charge could leak from our normal 3-dimensional space into hidden extra dimensions.
s that would be allowed if electric charge is not always conserved. No such decays have ever been seen.
The best experimental test comes from searches for the energetic photon from an electron
decaying into a neutrino
and a single photon
:
but there are theoretical arguments that such single-photon decays will never occur even if charge is not conserved.
Charge disappearance tests are sensitive to decays without energetic photons, other unusual charge violating processes such as an electron spontaneously changing into a positron
,
and to electric charge moving into other dimensions.
The best experimental bounds on charge disappearance are:
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, charge conservation is the principle that electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved
Conserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
. The first written statement of the principle was by American scientist and statesman Benjamin Franklin
Benjamin Franklin
Dr. Benjamin Franklin was one of the Founding Fathers of the United States. A noted polymath, Franklin was a leading author, printer, political theorist, politician, postmaster, scientist, musician, inventor, satirist, civic activist, statesman, and diplomat...
in 1747.
Charge conservation is a physical law that states that the change in the amount of electric charge in any volume of space is exactly equal to the amount of charge flowing into the volume minus the amount of charge flowing out of the volume. In essence, charge conservation is an accounting relationship between the amount of charge in a region and the flow of charge into and out of that region.
Mathematically, we can state the law as a continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
:
Q(t) is the quantity of electric charge in a specific volume at time t, QIN is
the amount of charge flowing into the volume between time t1 and t2, and QOUT is the amount of charge flowing out of the volume during the same time period.
This does not mean that individual positive and negative charges cannot be created or destroyed. Electric charge is carried by subatomic particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
s such as electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s and proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, which can be created and destroyed. In particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, charge conservation means that in elementary particle reactions that create charged particles, equal numbers of positive and negative particles are always created, keeping the net amount of charge unchanged. Similarly, when particles are destroyed, equal numbers of positive and negative charges are destroyed.
Although conservation of charge requires that the total quantity of charge in the universe is constant, it leaves open the question of what that quantity is. Most evidence indicates that the total charge in the universe is zero; that is, there are equal quantities of positive and negative charge.
Formal statement of the law
Vector calculus can be used to express the law in terms of charge densityCharge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
ρ (in coulombs per cubic meter) and electric current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
J (in amperes per square meter):
This statement is equivalent to a conservation of four-current
Four-current
In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
. In the mid-nineteenth century, James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
postulated the existence of electromagnetic waves as a result of his discovery that Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
(in its original form) was inconsistent with the conservation of charge. After correctly reformulating Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
, Maxwell also realized that such waves would travel at the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, and that light itself must be a form of electromagnetic radiation. See electromagnetic wave equation
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
for a full discussion of these discoveries.
Mathematical derivation
The net current into a volume iswhere S = ∂V is the boundary of V oriented by outward-pointing normals
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
, and dS is shorthand for NdS, the outward pointing normal of the boundary ∂V. Here
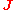is the current density (charge per unit area per unit time) at the surface of the volume. The vector points in the direction of the current.From the Divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
this can be written
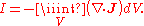
Charge conservation requires that the net current into a volume must necessarily equal the net change in charge within the volume.
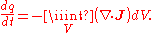
Charge is related to charge density by the relation
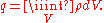
This yields
Since this is true for every volume, we have in general
Connection to gauge invariance
Charge conservation can also be understood as a consequence of symmetry through Noether's theoremNoether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, a central result in theoretical physics that asserts that each conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
is associated with a symmetry
Symmetry in physics
In physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
of the underlying physics. The symmetry that is associated with charge conservation is the global gauge invariance of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. This is related to the fact that the electric and magnetic fields are not changed by different choices of the value representing the zero point of electrostatic potential
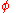. However the full symmetry is more complicated, and also involves the vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
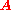. The full statement of gauge invariance is that the physics of an electromagnetic field are unchanged when the scalar and vector potential are shifted by the gradient of an arbitrary scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
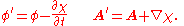
:In quantum mechanics the scalar field is equivalent to a phase shift in the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of the charged particle:
so gauge invariance is equivalent to the well known fact that changes in the phase of a wavefunction are unobservable, and only changes in the magnitude of the wavefunction result in changes to the probability function
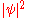. This is the ultimate theoretical origin of charge conservation.Gauge invariance is a very important, well established property of the electromagnetic field and has many testable consequences. The theoretical justification for charge conservation is greatly strengthened by being linked to this symmetry. For example, local gauge invariance also requires that the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
be massless, so the good experimental evidence that the photon has zero mass is also strong evidence that charge is conserved.
Even if gauge symmetry is exact, however, there might be apparent electric charge non-conservation if charge could leak from our normal 3-dimensional space into hidden extra dimensions.
Experimental Evidence
The best experimental tests of electric charge conservation are searches for particle decayParticle decay
Particle decay is the spontaneous process of one elementary particle transforming into other elementary particles. During this process, an elementary particle becomes a different particle with less mass and an intermediate particle such as W boson in muon decay. The intermediate particle then...
s that would be allowed if electric charge is not always conserved. No such decays have ever been seen.
The best experimental test comes from searches for the energetic photon from an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
decaying into a neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
and a single photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
:
| e → νγ | mean lifetime is greater than 4.6 × 1026years (90% Confidence Level), |
but there are theoretical arguments that such single-photon decays will never occur even if charge is not conserved.
Charge disappearance tests are sensitive to decays without energetic photons, other unusual charge violating processes such as an electron spontaneously changing into a positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
,
and to electric charge moving into other dimensions.
The best experimental bounds on charge disappearance are:
| e → anything | mean lifetime is greater than 6.4 × 1024years (68% CL) | |
| n → pν | charge non-conserving decays are less than 8 × 10−27 (68% CL) of all neutron Neutron The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of... decays |
See also
- CapacitorCapacitorA capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
– device for storing electric charge - Conservation Laws and Symmetry
- Introduction to Gauge Theory – includes further discussion of gauge invariance and charge conservation
- Kirchhoff's circuit lawsKirchhoff's circuit lawsKirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
- application of charge conservation to electric circuits - Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...