Inertial frame of reference
Encyclopedia
In physics
, an inertial frame of reference (also inertial reference frame or inertial frame or Galilean reference frame) is a frame of reference
that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.
All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not accelerating (in the sense of proper acceleration
that would be detected by an accelerometer
). Measurements in one inertial frame can be converted to measurements in another by a simple transformation (the Galilean transformation
in Newtonian physics and the Lorentz transformation
in special relativity). In general relativity
, an inertial reference frame is only an approximation that applies in a region that is small enough for the curvature of space to be negligible.
Physical laws take the same form in all inertial frames. In a non-inertial reference frame
the laws of physics depend upon the acceleration of that frame of reference, and the usual physical forces must be supplemented by fictitious force
s. For example, a ball dropped towards the ground does not go exactly straight down because the Earth
is rotating. Someone rotating with the Earth
must include the Coriolis force to predict the horizontal motion. Another example of a fictitious force associated with rotating reference frames is the centrifugal force
.
. If the coordinates are chosen badly, the laws of motion may be more complex than necessary. For example, suppose a free body (one having no external forces on it) is at rest at some instant. In many coordinate systems, it would begin to move at the next instant, even though there are no forces on it. However, a frame of reference can always be chosen in which it remains stationary. Similarly, if space is not described uniformly or time independently, a coordinate system could describe the simple flight of a free body in space as a complicated zig-zag in its coordinate system. Indeed, an intuitive summary of inertial frames can be given as: In an inertial reference frame, the laws of mechanics take their simplest form.
In an inertial frame, Newton's first law (the law of inertia) is satisfied: Any free motion has a constant magnitude and direction. Newton's second law for a particle
takes the form:

with F the net force (a vector), m the mass of a particle and a the acceleration
of the particle (also a vector) which would be measured by an observer at rest in the frame. The force F is the vector sum of all "real" forces on the particle, such as electromagnetic, gravitational, nuclear and so forth. In contrast, Newton's second law in a rotating frame of reference, rotating at angular rate Ω about an axis, takes the form:

which looks the same as in an inertial frame, but now the force F′ is the resultant of not only F, but also additional terms (the paragraph following this equation presents the main points without detailed mathematics):

where the angular rotation of the frame is expressed by the vector Ω pointing in the direction of the axis of rotation, and with magnitude equal to the angular rate of rotation Ω, symbol × denotes the vector cross product, vector xB locates the body and vector vB is the velocity
of the body according to a rotating observer (different from the velocity seen by the inertial observer).
The extra terms in the force F′ are the "fictitious" forces for this frame. (The first extra term is the Coriolis force, the second the centrifugal force, and the third the Euler force
.) These terms all have these properties: they vanish when Ω = 0; that is, they are zero for an inertial frame (which, of course, does not rotate); they take on a different magnitude and direction in every rotating frame, depending upon its particular value of Ω; they are ubiquitous in the rotating frame (affect every particle, regardless of circumstance); and they have no apparent source in identifiable physical sources, in particular, matter
. Also, fictitious forces do not drop off with distance (unlike, for example, nuclear force
s or electrical forces). For example, the centrifugal force that appears to emanate from the axis of rotation in a rotating frame increases with distance from the axis.
All observers agree on the real forces, F; only non-inertial observers need fictitious forces. The laws of physics in the inertial frame are simpler because unnecessary forces are not present.
In Newton's time the fixed stars were invoked as a reference frame, supposedly at rest relative to absolute space. In reference frames that were either at rest with respect to the fixed stars or in uniform translation relative to these stars, Newton's laws of motion
were supposed to hold. In contrast, in frames accelerating with respect to the fixed stars, an important case being frames rotating relative to the fixed stars, the laws of motion did not hold in their simplest form, but had to be supplemented by the addition of fictitious forces, for example, the Coriolis force and the centrifugal force
. Two interesting experiments were devised by Newton to demonstrate how these forces could be discovered, thereby revealing to an observer that they were not in an inertial frame: the example of the tension in the cord linking two spheres rotating
about their center of gravity, and the example of the curvature of the surface of water in a rotating bucket
. In both cases, application of Newton's second law would not work for the rotating observer without invoking centrifugal and Coriolis forces to account for their observations (tension in the case of the spheres; parabolic water surface in the case of the rotating bucket).
As we now know, the fixed stars are not fixed. Those that reside in the Milky Way
turn with the galaxy, exhibiting proper motion
s. Those that are outside our galaxy (such as nebulae once mistaken to be stars) participate in their own motion as well, partly due to expansion of the universe, and partly due to peculiar velocities
. (The Andromeda galaxy
is on collision course with the Milky Way
at a speed of 117 km/s.) The concept of inertial frames of reference is no longer tied to either the fixed stars or to absolute space. Rather, the identification of an inertial frame is based upon the simplicity of the laws of physics in the frame. In particular, the absence of fictitious forces is their identifying property.
In practice, although not a requirement, using a frame of reference based upon the fixed stars as though it were an inertial frame of reference introduces very little discrepancy. For example, the centrifugal acceleration of the Earth because of its rotation about the Sun is about thirty million times greater than that of the Sun about the galactic center.
To illustrate further, consider the question: "Does our Universe rotate?" To answer, we might attempt to explain the shape of the Milky Way
galaxy using the laws of physics. (Other observations might be more definitive (that is, provide larger discrepancies
or less measurement uncertainty
), like the anisotropy of the microwave background radiation or Big Bang nucleosynthesis
.) Just how flat the disc of the Milky Way is depends on its rate of rotation in a inertial frame of reference. If we attribute its apparent rate of rotation entirely to rotation in an inertial frame, a different "flatness" is predicted than if we suppose part of this rotation actually is due to rotation of the Universe and should not be included in the rotation of the galaxy itself. Based upon the laws of physics, a model is set up in which one parameter is the rate of rotation of the Universe. If the laws of physics agree more accurately with observations in a model with rotation than without it, we are inclined to select the best-fit value for rotation, subject to all other pertinent experimental observations. If no value of the rotation parameter is successful and theory is not within observational error, a modification of physical law is considered. (For example, dark matter
is invoked to explain the galactic rotation curve.) So far, observations show any rotation of the Universe is very slow (no faster than once every 60·1012 years (10−13 rad/yr)), and debate persists over whether there is any rotation. However, if rotation were found, interpretation of observations in a frame tied to the Universe would have to be corrected for the fictitious forces inherent in such rotation. Evidently, such an approach adopts the view that "an inertial frame of reference is one where our laws of physics apply" (or need the least modification).
, all physical laws take their simplest form in an inertial frame, and there exist multiple inertial frames interrelated by uniform translation
:
The principle of simplicity can be used within Newtonian physics as well as in special relativity; see Nagel and also Blagojević.
In practical terms, the equivalence of inertial reference frames means that scientists within a box moving uniformly cannot determine their absolute velocity by any experiment (otherwise the differences would set up an absolute standard reference frame). According to this definition, supplemented with the constancy of the speed of light, inertial frames of reference transform among themselves according to the Poincaré group
of symmetry transformations, of which the Lorentz transformation
s are a subgroup. In Newtonian mechanics, which can be viewed as a limiting case of special relativity in which the speed of light is infinite, inertial frames of reference are related by the Galilean group of symmetries.
Indeed, the expression inertial frame of reference was coined by Ludwig Lange
in 1885, to replace Newton's definitions of "absolute space and time" by a more operational definition. As referenced by Iro, Lange proposed:
A discussion of Lange's proposal can be found in Mach.
The inadequacy of the notion of "absolute space" in Newtonian mechanics is spelled out by Blagojević:
The utility of operational definitions was carried much further in the special theory of relativity. Some historical background including Lange's definition is provided by DiSalle, who says in summary:
 Within the realm of Newtonian mechanics, an inertia
Within the realm of Newtonian mechanics, an inertia
l frame of reference, or inertial reference frame, is one in which Newton's first law of motion is valid. However, the principle of special relativity generalizes the notion of inertial frame to include all physical laws, not simply Newton's first law.
Newton viewed the first law as valid in any reference frame that is in uniform motion relative to the fixed stars; that is, neither rotating nor accelerating relative to the stars. Today the notion of "absolute space" is abandoned, and an inertial frame in the field of classical mechanics
is defined as:
Hence, with respect to an inertial frame, an object or body accelerates
only when a physical force
is applied, and (following Newton's first law of motion
), in the absence of a net force, a body at rest
will remain at rest and a body in motion will continue to move uniformly—that is, in a straight line and at constant speed
. Newtonian inertial frames transform among each other according to the Galilean group of symmetries.
If this rule is interpreted as saying that straight-line motion is an indication of zero net force, the rule does not identify inertial reference frames, because straight-line motion can be observed in a variety of frames. If the rule is interpreted as defining an inertial frame, then we have to be able to determine when zero net force is applied. The problem was summarized by Einstein:
There are several approaches to this issue. One approach is to argue that all real forces drop off with distance from their sources in a known manner, so we have only to be sure that we are far enough away from all sources to ensure that no force is present. A possible issue with this approach is the historically long-lived view that the distant universe might affect matters (Mach's principle
). Another approach is to identify all real sources for real forces and account for them. A possible issue with this approach is that we might miss something, or account inappropriately for their influence (Mach's principle again?). A third approach is to look at the way the forces transform when we shift reference frames. Fictitious forces, those that arise due to the acceleration of a frame, disappear in inertial frames, and have complicated rules of transformation in general cases. On the basis of universality of physical law and the request for frames where the laws are most simply expressed, inertial frames are distinguished by the absence of such fictitious forces.
Newton enunciated a principle of relativity himself in one of his corollaries to the laws of motion:
This principle differs from the special principle in two ways: first, it is restricted to mechanics, and second, it makes no mention of simplicity. It shares with the special principle the invariance of the form of the description among mutually translating reference frames. The role of fictitious forces in classifying reference frames is pursued further below.
 Inertial and non-inertial reference frames can be distinguished by the absence or presence of fictitious force
Inertial and non-inertial reference frames can be distinguished by the absence or presence of fictitious force
s, as explained shortly. The presence of fictitious forces indicates the physical laws are not the simplest laws available so, in terms of the special principle of relativity, a frame where fictitious forces are present is not an inertial frame:
Bodies in non-inertial reference frame
s are subject to so-called fictitious forces (pseudo-forces); that is, force
s that result from the acceleration of the reference frame
itself and not from any physical force acting on the body. Examples of fictitious forces are the centrifugal force and the Coriolis force in rotating reference frame
s.
How then, are "fictitious' forces to be separated from "real" forces? It is hard to apply the Newtonian definition of an inertial frame without this separation. For example, consider a stationary object in an inertial frame. Being at rest, no net force is applied. But in a frame rotating about a fixed axis, the object appears to move in a circle, and is subject to centripetal force (which is made up of the Coriolis force and the centrifugal force). How can we decide that the rotating frame is a non-inertial frame? There are two approaches to this resolution: one approach is to look for the origin of the fictitious forces (the Coriolis force and the centrifugal force). We will find there are no sources for these forces, no associated force carrier
s, no originating bodies. A second approach is to look at a variety of frames of reference. For any inertial frame, the Coriolis force and the centrifugal force disappear, so application of the principle of special relativity would identify these frames where the forces disappear as sharing the same and the simplest physical laws, and hence rule that the rotating frame is not an inertial frame.
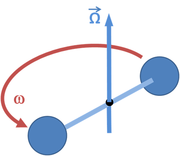
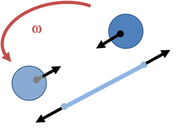
Newton examined this problem himself using rotating spheres, as shown in Figure 2 and Figure 3. He pointed out that if the spheres are not rotating, the tension in the tying string is measured as zero in every frame of reference. If the spheres only appear to rotate (that is, we are watching stationary spheres from a rotating frame), the zero tension in the string is accounted for by observing that the centripetal force is supplied by the centrifugal and Coriolis forces in combination, so no tension is needed. If the spheres really are rotating, the tension observed is exactly the centripetal force required by the circular motion. Thus, measurement of the tension in the string identifies the inertial frame: it is the one where the tension in the string provides exactly the centripetal force demanded by the motion as it is observed in that frame, and not a different value. That is, the inertial frame is the one where the fictitious forces vanish.
So much for fictitious forces due to rotation. However, for linear acceleration, Newton expressed the idea of undetectability of straight-line accelerations held in common:
This principle generalizes the notion of an inertial frame. For example, an observer confined in a free-falling lift will assert that he himself is a valid inertial frame, even if he is accelerating under gravity, so long as he has no knowledge about anything outside the lift. So, strictly speaking, inertial frame is a relative concept. With this in mind, we can define inertial frames collectively as a set of frames which are stationary or moving at constant velocity with respect to each other, so that a single inertial frame is defined as an element of this set.
For these ideas to apply, everything observed in the frame has to be subject to a base-line, common acceleration shared by the frame itself. That situation would apply, for example, to the elevator example, where all objects are subject to the same gravitational acceleration, and the elevator itself accelerates at the same rate.
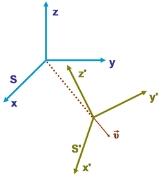
, which includes relativity, assumes the equivalence of all inertial reference frames. Newtonian mechanics makes the additional assumptions of absolute space and absolute time. Given these two assumptions, the coordinates of the same event (a point in space and time) described in two inertial reference frames are related by a Galilean transformation.


where r0 and t0 represent shifts in the origin of space and time, and v is the relative velocity of the two inertial reference frames. Under Galilean transformations, the time t2 − t1 between two events is the same for all inertial reference frames and the distance
between two simultaneous events (or, equivalently, the length of any object, |r2 − r1|) is also the same.
theory of special relativity
, like Newtonian mechanics, assumes the equivalence of all inertial reference frames, but makes an additional assumption, foreign to Newtonian mechanics, namely, that in free space light always is propagated with the speed of light
c0, a defined value independent of its direction of propagation and its frequency, and also independent of the state of motion of the emitting body. This second assumption has been verified experimentally and leads to counter-intuitive deductions including:
These deductions are logical consequences of the stated assumptions, and are general properties of space-time, typically without regard to a consideration of properties pertaining to the structure of individual objects like atoms or stars, nor to the mechanisms of clocks.
These effects are expressed mathematically by the Lorentz transformation




where shifts in origin have been ignored, the relative velocity is assumed to be in the -direction and the Lorentz factor
-direction and the Lorentz factor
γ is defined by:

The Lorentz transformation is equivalent to the Galilean transformation
in the limit c0 → ∞ (a hypothetical case) or v → 0 (low speeds).
Under Lorentz transformation
s, the time and distance between events may differ among inertial reference frames; however, the Lorentz scalar
distance s between two events is the same in all inertial reference frames

From this perspective, the speed of light
is only accidentally a property of light
, and is rather a property of spacetime
, a conversion factor
between conventional time units (such as second
s) and length units (such as meters).
Incidentally, because of the limitations on speeds faster than the speed of light, notice that a rotating frame of reference (which is a non-inertial frame, of course) cannot be used out to arbitrary distances because at large radius its components would move faster than the speed of light.
This idea was introduced in Einstein's 1907 article "Principle of Relativity and Gravitation" and later developed in 1911. Support for this principle is found in the Eötvös experiment
, which determines whether the ratio of inertial to gravitational mass is the same for all bodies, regardless of size or composition. To date no difference has been found to a few parts in 1011. For some discussion of the subtleties of the Eötvös experiment, such as the local mass distribution around the experimental site (including a quip about the mass of Eötvös himself), see Franklin.
Einstein’s general theory
modifies the distinction between nominally "inertial" and "noninertial" effects by replacing special relativity's "flat" Euclidean geometry
with a curved metric. In general relativity, the principle of inertia is replaced with the principle of geodesic motion
, whereby objects move in a way dictated by the curvature of spacetime. As a consequence of this curvature, it is not a given in general relativity that inertial objects moving at a particular rate with respect to each other will continue to do so. This phenomenon of geodesic deviation means that inertial frames of reference do not exist globally as they do in Newtonian mechanics and special relativity.
However, the general theory reduces to the special theory over sufficiently small regions of spacetime, where curvature effects become less important and the earlier inertial frame arguments can come back into play. Consequently, modern special relativity is now sometimes described as only a “local theory”. (However, this refers to the theory’s application rather than to its derivation.)
Rotation of the Universe
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, an inertial frame of reference (also inertial reference frame or inertial frame or Galilean reference frame) is a frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.
All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not accelerating (in the sense of proper acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
that would be detected by an accelerometer
Accelerometer
An accelerometer is a device that measures proper acceleration, also called the four-acceleration. This is not necessarily the same as the coordinate acceleration , but is rather the type of acceleration associated with the phenomenon of weight experienced by a test mass that resides in the frame...
). Measurements in one inertial frame can be converted to measurements in another by a simple transformation (the Galilean transformation
Galilean transformation
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...
in Newtonian physics and the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
in special relativity). In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, an inertial reference frame is only an approximation that applies in a region that is small enough for the curvature of space to be negligible.
Physical laws take the same form in all inertial frames. In a non-inertial reference frame
Non-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
the laws of physics depend upon the acceleration of that frame of reference, and the usual physical forces must be supplemented by fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s. For example, a ball dropped towards the ground does not go exactly straight down because the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is rotating. Someone rotating with the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
must include the Coriolis force to predict the horizontal motion. Another example of a fictitious force associated with rotating reference frames is the centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
.
Introduction
The motion of a body can only be described relative to something else - other bodies, observers, or a set of space-time coordinates. These are called frames of referenceFrame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
. If the coordinates are chosen badly, the laws of motion may be more complex than necessary. For example, suppose a free body (one having no external forces on it) is at rest at some instant. In many coordinate systems, it would begin to move at the next instant, even though there are no forces on it. However, a frame of reference can always be chosen in which it remains stationary. Similarly, if space is not described uniformly or time independently, a coordinate system could describe the simple flight of a free body in space as a complicated zig-zag in its coordinate system. Indeed, an intuitive summary of inertial frames can be given as: In an inertial reference frame, the laws of mechanics take their simplest form.
In an inertial frame, Newton's first law (the law of inertia) is satisfied: Any free motion has a constant magnitude and direction. Newton's second law for a particle
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
takes the form:

with F the net force (a vector), m the mass of a particle and a the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of the particle (also a vector) which would be measured by an observer at rest in the frame. The force F is the vector sum of all "real" forces on the particle, such as electromagnetic, gravitational, nuclear and so forth. In contrast, Newton's second law in a rotating frame of reference, rotating at angular rate Ω about an axis, takes the form:

which looks the same as in an inertial frame, but now the force F′ is the resultant of not only F, but also additional terms (the paragraph following this equation presents the main points without detailed mathematics):

where the angular rotation of the frame is expressed by the vector Ω pointing in the direction of the axis of rotation, and with magnitude equal to the angular rate of rotation Ω, symbol × denotes the vector cross product, vector xB locates the body and vector vB is the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the body according to a rotating observer (different from the velocity seen by the inertial observer).
The extra terms in the force F′ are the "fictitious" forces for this frame. (The first extra term is the Coriolis force, the second the centrifugal force, and the third the Euler force
Euler force
In classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
.) These terms all have these properties: they vanish when Ω = 0; that is, they are zero for an inertial frame (which, of course, does not rotate); they take on a different magnitude and direction in every rotating frame, depending upon its particular value of Ω; they are ubiquitous in the rotating frame (affect every particle, regardless of circumstance); and they have no apparent source in identifiable physical sources, in particular, matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
. Also, fictitious forces do not drop off with distance (unlike, for example, nuclear force
Nuclear force
The nuclear force is the force between two or more nucleons. It is responsible for binding of protons and neutrons into atomic nuclei. The energy released causes the masses of nuclei to be less than the total mass of the protons and neutrons which form them...
s or electrical forces). For example, the centrifugal force that appears to emanate from the axis of rotation in a rotating frame increases with distance from the axis.
All observers agree on the real forces, F; only non-inertial observers need fictitious forces. The laws of physics in the inertial frame are simpler because unnecessary forces are not present.
In Newton's time the fixed stars were invoked as a reference frame, supposedly at rest relative to absolute space. In reference frames that were either at rest with respect to the fixed stars or in uniform translation relative to these stars, Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
were supposed to hold. In contrast, in frames accelerating with respect to the fixed stars, an important case being frames rotating relative to the fixed stars, the laws of motion did not hold in their simplest form, but had to be supplemented by the addition of fictitious forces, for example, the Coriolis force and the centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
. Two interesting experiments were devised by Newton to demonstrate how these forces could be discovered, thereby revealing to an observer that they were not in an inertial frame: the example of the tension in the cord linking two spheres rotating
Rotating spheres
Isaac Newton's rotating spheres argument attempts to demonstrate that true rotational motion can be defined by observing the tension in the string joining two identical spheres...
about their center of gravity, and the example of the curvature of the surface of water in a rotating bucket
Bucket argument
Isaac Newton's rotating bucket argument was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies...
. In both cases, application of Newton's second law would not work for the rotating observer without invoking centrifugal and Coriolis forces to account for their observations (tension in the case of the spheres; parabolic water surface in the case of the rotating bucket).
As we now know, the fixed stars are not fixed. Those that reside in the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
turn with the galaxy, exhibiting proper motion
Proper motion
The proper motion of a star is its angular change in position over time as seen from the center of mass of the solar system. It is measured in seconds of arc per year, arcsec/yr, where 3600 arcseconds equal one degree. This contrasts with radial velocity, which is the time rate of change in...
s. Those that are outside our galaxy (such as nebulae once mistaken to be stars) participate in their own motion as well, partly due to expansion of the universe, and partly due to peculiar velocities
Peculiar velocity
Peculiar motion or peculiar velocity refers to the true velocity of an object, relative to a rest frame.-Galactic astronomy:In galactic astronomy, the term peculiar motion refers to the motion of an object through space.Local objects are usually related in terms of proper motion and radial...
. (The Andromeda galaxy
Andromeda Galaxy
The Andromeda Galaxy is a spiral galaxy approximately 2.5 million light-years from Earth in the constellation Andromeda. It is also known as Messier 31, M31, or NGC 224, and is often referred to as the Great Andromeda Nebula in older texts. Andromeda is the nearest spiral galaxy to the...
is on collision course with the Milky Way
Andromeda-Milky Way collision
The collision seen from a hypothetical extragalactic planet. The galaxies will be at this relative angleThe Andromeda–Milky Way collision is a predicted galaxy collision that could possibly take place in approximately 3 to 5 billion years' time between the two largest galaxies in the Local...
at a speed of 117 km/s.) The concept of inertial frames of reference is no longer tied to either the fixed stars or to absolute space. Rather, the identification of an inertial frame is based upon the simplicity of the laws of physics in the frame. In particular, the absence of fictitious forces is their identifying property.
In practice, although not a requirement, using a frame of reference based upon the fixed stars as though it were an inertial frame of reference introduces very little discrepancy. For example, the centrifugal acceleration of the Earth because of its rotation about the Sun is about thirty million times greater than that of the Sun about the galactic center.
To illustrate further, consider the question: "Does our Universe rotate?" To answer, we might attempt to explain the shape of the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
galaxy using the laws of physics. (Other observations might be more definitive (that is, provide larger discrepancies
Observational error
Observational error is the difference between a measured value of quantity and its true value. In statistics, an error is not a "mistake". Variability is an inherent part of things being measured and of the measurement process.-Science and experiments:...
or less measurement uncertainty
Measurement uncertainty
In metrology, measurement uncertainty is a non-negative parameter characterizing the dispersion of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured...
), like the anisotropy of the microwave background radiation or Big Bang nucleosynthesis
Big Bang nucleosynthesis
In physical cosmology, Big Bang nucleosynthesis refers to the production of nuclei other than those of H-1 during the early phases of the universe...
.) Just how flat the disc of the Milky Way is depends on its rate of rotation in a inertial frame of reference. If we attribute its apparent rate of rotation entirely to rotation in an inertial frame, a different "flatness" is predicted than if we suppose part of this rotation actually is due to rotation of the Universe and should not be included in the rotation of the galaxy itself. Based upon the laws of physics, a model is set up in which one parameter is the rate of rotation of the Universe. If the laws of physics agree more accurately with observations in a model with rotation than without it, we are inclined to select the best-fit value for rotation, subject to all other pertinent experimental observations. If no value of the rotation parameter is successful and theory is not within observational error, a modification of physical law is considered. (For example, dark matter
Dark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
is invoked to explain the galactic rotation curve.) So far, observations show any rotation of the Universe is very slow (no faster than once every 60·1012 years (10−13 rad/yr)), and debate persists over whether there is any rotation. However, if rotation were found, interpretation of observations in a frame tied to the Universe would have to be corrected for the fictitious forces inherent in such rotation. Evidently, such an approach adopts the view that "an inertial frame of reference is one where our laws of physics apply" (or need the least modification).
Background
A brief comparison of inertial frames in special relativity and in Newtonian mechanics, and the role of absolute space is next.A set of frames where the laws of physics are simple
According to the first postulate of special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, all physical laws take their simplest form in an inertial frame, and there exist multiple inertial frames interrelated by uniform translation
Translation (physics)
In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
:
The principle of simplicity can be used within Newtonian physics as well as in special relativity; see Nagel and also Blagojević.
In practical terms, the equivalence of inertial reference frames means that scientists within a box moving uniformly cannot determine their absolute velocity by any experiment (otherwise the differences would set up an absolute standard reference frame). According to this definition, supplemented with the constancy of the speed of light, inertial frames of reference transform among themselves according to the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
of symmetry transformations, of which the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s are a subgroup. In Newtonian mechanics, which can be viewed as a limiting case of special relativity in which the speed of light is infinite, inertial frames of reference are related by the Galilean group of symmetries.
Absolute space
Newton posited an absolute space considered well approximated by a frame of reference stationary relative to the fixed stars. An inertial frame was then one in uniform translation relative to absolute space. However, some scientists (called "relativists" by Mach), even at the time of Newton, felt that absolute space was a defect of the formulation, and should be replaced.Indeed, the expression inertial frame of reference was coined by Ludwig Lange
Ludwig Lange
Ludwig Lange was a German physicist.-Biography:He was the son of the philologist and archaeologist Ludwig Lange and his wife Adelheide Blume. He studied mathematics, physics, and also psychology, epistemology, ethics at the University of Leipzig and the University of Gießen from 1882-1885...
in 1885, to replace Newton's definitions of "absolute space and time" by a more operational definition. As referenced by Iro, Lange proposed:
A discussion of Lange's proposal can be found in Mach.
The inadequacy of the notion of "absolute space" in Newtonian mechanics is spelled out by Blagojević:
The utility of operational definitions was carried much further in the special theory of relativity. Some historical background including Lange's definition is provided by DiSalle, who says in summary:
Newton's inertial frame of reference

Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
l frame of reference, or inertial reference frame, is one in which Newton's first law of motion is valid. However, the principle of special relativity generalizes the notion of inertial frame to include all physical laws, not simply Newton's first law.
Newton viewed the first law as valid in any reference frame that is in uniform motion relative to the fixed stars; that is, neither rotating nor accelerating relative to the stars. Today the notion of "absolute space" is abandoned, and an inertial frame in the field of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
is defined as:
Hence, with respect to an inertial frame, an object or body accelerates
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
only when a physical force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
is applied, and (following Newton's first law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
), in the absence of a net force, a body at rest
Rest (physics)
Rest in physics refers to an object being stationary relative to a particular frame of reference or another object. According to the theory of relativity it is said that an object is: at rest relative to another. For example, a train decelerates on approach to a station and eventually stops...
will remain at rest and a body in motion will continue to move uniformly—that is, in a straight line and at constant speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
. Newtonian inertial frames transform among each other according to the Galilean group of symmetries.
If this rule is interpreted as saying that straight-line motion is an indication of zero net force, the rule does not identify inertial reference frames, because straight-line motion can be observed in a variety of frames. If the rule is interpreted as defining an inertial frame, then we have to be able to determine when zero net force is applied. The problem was summarized by Einstein:
There are several approaches to this issue. One approach is to argue that all real forces drop off with distance from their sources in a known manner, so we have only to be sure that we are far enough away from all sources to ensure that no force is present. A possible issue with this approach is the historically long-lived view that the distant universe might affect matters (Mach's principle
Mach's principle
In theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
). Another approach is to identify all real sources for real forces and account for them. A possible issue with this approach is that we might miss something, or account inappropriately for their influence (Mach's principle again?). A third approach is to look at the way the forces transform when we shift reference frames. Fictitious forces, those that arise due to the acceleration of a frame, disappear in inertial frames, and have complicated rules of transformation in general cases. On the basis of universality of physical law and the request for frames where the laws are most simply expressed, inertial frames are distinguished by the absence of such fictitious forces.
Newton enunciated a principle of relativity himself in one of his corollaries to the laws of motion:
This principle differs from the special principle in two ways: first, it is restricted to mechanics, and second, it makes no mention of simplicity. It shares with the special principle the invariance of the form of the description among mutually translating reference frames. The role of fictitious forces in classifying reference frames is pursued further below.
Separating non-inertial from inertial reference frames


Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s, as explained shortly. The presence of fictitious forces indicates the physical laws are not the simplest laws available so, in terms of the special principle of relativity, a frame where fictitious forces are present is not an inertial frame:
Bodies in non-inertial reference frame
Non-inertial reference frame
A non-inertial reference frame is a frame of reference that is under acceleration. The laws of physics in such a frame do not take on their most simple form, as required by the theory of special relativity...
s are subject to so-called fictitious forces (pseudo-forces); that is, force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s that result from the acceleration of the reference frame
Reference frame
Reference frame may refer to:*Frame of reference, in physics*Reference frame , frames of a compressed video that are used to define future frames...
itself and not from any physical force acting on the body. Examples of fictitious forces are the centrifugal force and the Coriolis force in rotating reference frame
Rotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. A rotating frame of reference is a special case of a non-inertial reference...
s.
How then, are "fictitious' forces to be separated from "real" forces? It is hard to apply the Newtonian definition of an inertial frame without this separation. For example, consider a stationary object in an inertial frame. Being at rest, no net force is applied. But in a frame rotating about a fixed axis, the object appears to move in a circle, and is subject to centripetal force (which is made up of the Coriolis force and the centrifugal force). How can we decide that the rotating frame is a non-inertial frame? There are two approaches to this resolution: one approach is to look for the origin of the fictitious forces (the Coriolis force and the centrifugal force). We will find there are no sources for these forces, no associated force carrier
Force carrier
In particle physics, quantum field theories such as the Standard Model describe nature in terms of fields. Each field has a complementary description as the set of particles of a particular type...
s, no originating bodies. A second approach is to look at a variety of frames of reference. For any inertial frame, the Coriolis force and the centrifugal force disappear, so application of the principle of special relativity would identify these frames where the forces disappear as sharing the same and the simplest physical laws, and hence rule that the rotating frame is not an inertial frame.
Newton examined this problem himself using rotating spheres, as shown in Figure 2 and Figure 3. He pointed out that if the spheres are not rotating, the tension in the tying string is measured as zero in every frame of reference. If the spheres only appear to rotate (that is, we are watching stationary spheres from a rotating frame), the zero tension in the string is accounted for by observing that the centripetal force is supplied by the centrifugal and Coriolis forces in combination, so no tension is needed. If the spheres really are rotating, the tension observed is exactly the centripetal force required by the circular motion. Thus, measurement of the tension in the string identifies the inertial frame: it is the one where the tension in the string provides exactly the centripetal force demanded by the motion as it is observed in that frame, and not a different value. That is, the inertial frame is the one where the fictitious forces vanish.
So much for fictitious forces due to rotation. However, for linear acceleration, Newton expressed the idea of undetectability of straight-line accelerations held in common:
This principle generalizes the notion of an inertial frame. For example, an observer confined in a free-falling lift will assert that he himself is a valid inertial frame, even if he is accelerating under gravity, so long as he has no knowledge about anything outside the lift. So, strictly speaking, inertial frame is a relative concept. With this in mind, we can define inertial frames collectively as a set of frames which are stationary or moving at constant velocity with respect to each other, so that a single inertial frame is defined as an element of this set.
For these ideas to apply, everything observed in the frame has to be subject to a base-line, common acceleration shared by the frame itself. That situation would apply, for example, to the elevator example, where all objects are subject to the same gravitational acceleration, and the elevator itself accelerates at the same rate.
Newtonian mechanics
Classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, which includes relativity, assumes the equivalence of all inertial reference frames. Newtonian mechanics makes the additional assumptions of absolute space and absolute time. Given these two assumptions, the coordinates of the same event (a point in space and time) described in two inertial reference frames are related by a Galilean transformation.


where r0 and t0 represent shifts in the origin of space and time, and v is the relative velocity of the two inertial reference frames. Under Galilean transformations, the time t2 − t1 between two events is the same for all inertial reference frames and the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between two simultaneous events (or, equivalently, the length of any object, |r2 − r1|) is also the same.
Special relativity
Einstein'sAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
theory of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, like Newtonian mechanics, assumes the equivalence of all inertial reference frames, but makes an additional assumption, foreign to Newtonian mechanics, namely, that in free space light always is propagated with the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c0, a defined value independent of its direction of propagation and its frequency, and also independent of the state of motion of the emitting body. This second assumption has been verified experimentally and leads to counter-intuitive deductions including:
- time dilationTime dilationIn the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
(moving clocks tick more slowly) - length contractionLength contractionIn physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
(moving objects are shortened in the direction of motion) - relativity of simultaneityRelativity of simultaneityIn physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
(simultaneous events in one reference frame are not simultaneous in almost all frames moving relative to the first).
These deductions are logical consequences of the stated assumptions, and are general properties of space-time, typically without regard to a consideration of properties pertaining to the structure of individual objects like atoms or stars, nor to the mechanisms of clocks.
These effects are expressed mathematically by the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...




where shifts in origin have been ignored, the relative velocity is assumed to be in the
 -direction and the Lorentz factor
-direction and the Lorentz factorLorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
γ is defined by:

The Lorentz transformation is equivalent to the Galilean transformation
Galilean transformation
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...
in the limit c0 → ∞ (a hypothetical case) or v → 0 (low speeds).
Under Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s, the time and distance between events may differ among inertial reference frames; however, the Lorentz scalar
Lorentz scalar
In physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
distance s between two events is the same in all inertial reference frames

From this perspective, the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is only accidentally a property of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
, and is rather a property of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, a conversion factor
Conversion of units
Conversion of units is the conversion between different units of measurement for the same quantity, typically through multiplicative conversion factors.- Process :...
between conventional time units (such as second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s) and length units (such as meters).
Incidentally, because of the limitations on speeds faster than the speed of light, notice that a rotating frame of reference (which is a non-inertial frame, of course) cannot be used out to arbitrary distances because at large radius its components would move faster than the speed of light.
General relativity
General relativity is based upon the principle of equivalence:This idea was introduced in Einstein's 1907 article "Principle of Relativity and Gravitation" and later developed in 1911. Support for this principle is found in the Eötvös experiment
Eötvös experiment
The Eötvös experiment was a famous physics experiment that measured the correlation between inertial mass and gravitational mass, demonstrating that the two were one and the same, something that had long been suspected but never demonstrated with the same accuracy. The earliest experiments were...
, which determines whether the ratio of inertial to gravitational mass is the same for all bodies, regardless of size or composition. To date no difference has been found to a few parts in 1011. For some discussion of the subtleties of the Eötvös experiment, such as the local mass distribution around the experimental site (including a quip about the mass of Eötvös himself), see Franklin.
Einstein’s general theory
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
modifies the distinction between nominally "inertial" and "noninertial" effects by replacing special relativity's "flat" Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
with a curved metric. In general relativity, the principle of inertia is replaced with the principle of geodesic motion
Geodesic (general relativity)
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational, force is a particular type of geodesic...
, whereby objects move in a way dictated by the curvature of spacetime. As a consequence of this curvature, it is not a given in general relativity that inertial objects moving at a particular rate with respect to each other will continue to do so. This phenomenon of geodesic deviation means that inertial frames of reference do not exist globally as they do in Newtonian mechanics and special relativity.
However, the general theory reduces to the special theory over sufficiently small regions of spacetime, where curvature effects become less important and the earlier inertial frame arguments can come back into play. Consequently, modern special relativity is now sometimes described as only a “local theory”. (However, this refers to the theory’s application rather than to its derivation.)
See also
- DiffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
- Galilean invarianceGalilean invarianceGalilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...
- General covarianceGeneral covarianceIn theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
- Local reference frameLocal reference frameIn theoretical physics, a local reference frame refers to a coordinate system or frame of reference that is only expected to function over a small region or a restricted region of space or spacetime....
- Lorentz invariance
- Newton's first law
Further reading
- Edwin F. TaylorEdwin F. TaylorEdwin F. Taylor is an American physicist known for his contributions to the teaching of physics. Taylor was editor of the American Journal of Physics, and is author of several introductory books to physics...
and John Archibald WheelerJohn Archibald WheelerJohn Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
, Spacetime Physics, 2nd ed. (Freeman, NY, 1992) - Albert EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, Relativity, the special and the general theories, 15th ed. (1954) - Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, (1900) "La theorie de Lorentz et la Principe de Reaction", Archives Neerlandaises, V, 253–78. - Albert EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, On the Electrodynamics of Moving Bodies, included in The Principle of Relativity, page 38. Dover 1923
Rotation of the Universe
- B Ciobanu, I Radinchi Modeling the electric and magnetic fields in a rotating universe Rom. Journ. Phys., Vol. 53, Nos. 1–2, P. 405–415, Bucharest, 2008
- Yuri N. Obukhov, Thoralf Chrobok, Mike Scherfner Shear-free rotating inflation Phys. Rev. D 66, 043518 (2002) [5 pages]
- Yuri N. Obukhov On physical foundations and observational effects of cosmic rotation (2000)
- Li-Xin Li Effect of the Global Rotation of the Universe on the Formation of Galaxies General Relativity and Gravitation, 30 (1998) doi: 10.1023/A:1018867011142
- P Birch Is the Universe rotating? Nature 298, 451 - 454 (29 July 1982)
- Kurt Gödel An example of a new type of cosmological solutions of Einstein’s field equations of gravitation Rev. Mod. Phys., Vol. 21, p. 447, 1949.
External links
- Stanford Encyclopedia of Philosophy entry
- Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.

