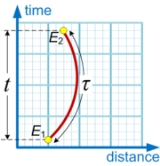
Proper time
Encyclopedia
In relativity
, proper time is the elapsed time
between two events
as measured by a clock
that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two events than that measured by a non-accelerated (inertial) clock between the same two events. The twin paradox
is an example of this effect.
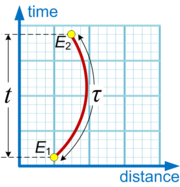 In terms of four-dimensional spacetime
In terms of four-dimensional spacetime
, proper time is analogous to arc length
in three-dimensional (Euclidean
) space.
By convention, proper time is usually represented by the Greek letter τ (tau
) to distinguish it from coordinate time represented by t or T.
By contrast, coordinate time
is the time between two events as measured by a distant observer using that observer's own method of assigning a time to an event. In the special case of an inertial observer in special relativity
, the time is measured using the observer's clock and the observer's definition of simultaneity.
A Euclidean geometrical analogy is that coordinate time is like distance measured with a straight vertical ruler
, whereas proper time is like distance measured with a tape measure
. If the tape measure is taut and vertical it measures the same as the ruler, but if the tape measure is not taut, or taut but not vertical, it will not measure the same as the ruler.
The concept of proper time was introduced by Hermann Minkowski
in 1908.
that represents a clock, observer, or test particle, and the metric structure
of that spacetime. Proper time is the pseudo-Riemannian
arc length of world line
s in four-dimensional spacetime.
From the mathematical point of view, coordinate time is assumed to be predefined and we require an expression for proper time as a function of coordinate time. From the experimental point of view, proper time is what is measured experimentally and then coordinate time is calculated from the proper time of some inertial clocks.
\int \sqrt {1 - \frac{1}{c^2} \left [ \left (\frac{dx}{dt}\right)^2 + \left (\frac{dy}{dt}\right)^2 + \left ( \frac{dz}{dt}\right)^2 \right] } \,dt,
where is the coordinate speed at coordinate time , and , , and are Cartesian spatial
coordinates.
If , , , and are all parameterised by a parameter
, this can be written as
In differential form it can be written as the line integral
where is the path of the clock in spacetime.
To make things even easier, inertial motion
in special relativity is where the spatial coordinates change at a constant rate with respect to the temporal coordinate. This further simplifies the proper time equation to
where Δ means "the change in" between two events.
The special relativity equations are special cases of the general case that follows.
as follows: Given a spacetime which is a pseudo-Riemannian manifold
mapped with a coordinate system
 and equipped with a corresponding metric tensor
and equipped with a corresponding metric tensor
 , the proper time
, the proper time  experienced in moving between two events along a timelike path P is given by the line integral
experienced in moving between two events along a timelike path P is given by the line integral
where
(Note: the Einstein summation convention is used in the above. The expression AμBμ is shorthand for , and the μ in Bμ denotes an index, not a power.)
This is referred to as the line element of the spacetime. s may be spacelike, lightlike, or timelike. Spacelike paths cannot be physically traveled (as they require moving faster than light). Lightlike paths can only be followed by light beams, for which there is no passage of proper time. Only timelike paths can be traveled by massive objects, in which case the invariant interval becomes the proper time . So for our purposes
. So for our purposes  .
.
Taking the square root of each side of the line element gives the above definition of . After that, take the line integral of each side to get
. After that, take the line integral of each side to get  as described by the first equation.
as described by the first equation.
spacetime is mapped with a four-vector
coordinate system where
where
This spacetime and mapping are described with the Minkowski metric:
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, proper time is the elapsed time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
between two events
Event (relativity)
In physics, and in particular relativity, an event indicates a physical situation or occurrence, located at a specific point in space and time. For example, a glass breaking on the floor is an event; it occurs at a unique place and a unique time, in a given frame of reference.Strictly speaking, the...
as measured by a clock
Clock
A clock is an instrument used to indicate, keep, and co-ordinate time. The word clock is derived ultimately from the Celtic words clagan and clocca meaning "bell". A silent instrument missing such a mechanism has traditionally been known as a timepiece...
that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two events than that measured by a non-accelerated (inertial) clock between the same two events. The twin paradox
Twin paradox
In physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...
is an example of this effect.

Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, proper time is analogous to arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
in three-dimensional (Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
) space.
By convention, proper time is usually represented by the Greek letter τ (tau
Tau
Tau is the 19th letter of the Greek alphabet. In the system of Greek numerals it has a value of 300.The name in English is pronounced , but in modern Greek it is...
) to distinguish it from coordinate time represented by t or T.
By contrast, coordinate time
Coordinate time
In the theory of relativity, it is convenient to express results in terms of a spacetime coordinate system relative to an implied observer. In many coordinate systems, an event is specified by one time coordinate and three spatial coordinates...
is the time between two events as measured by a distant observer using that observer's own method of assigning a time to an event. In the special case of an inertial observer in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, the time is measured using the observer's clock and the observer's definition of simultaneity.
A Euclidean geometrical analogy is that coordinate time is like distance measured with a straight vertical ruler
Ruler
A ruler, sometimes called a rule or line gauge, is an instrument used in geometry, technical drawing, printing and engineering/building to measure distances and/or to rule straight lines...
, whereas proper time is like distance measured with a tape measure
Tape measure
A tape measure or measuring tape is a flexible form of ruler. It consists of a ribbon of cloth, plastic, fiber glass, or metal strip with linear-measurement markings. It is a common measuring tool. Its flexibility allows for a measure of great length to be easily carried in pocket or toolkit and...
. If the tape measure is taut and vertical it measures the same as the ruler, but if the tape measure is not taut, or taut but not vertical, it will not measure the same as the ruler.
The concept of proper time was introduced by Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
in 1908.
Mathematical formalism
The formal definition of proper time involves describing the path through spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
that represents a clock, observer, or test particle, and the metric structure
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
of that spacetime. Proper time is the pseudo-Riemannian
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
arc length of world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s in four-dimensional spacetime.
From the mathematical point of view, coordinate time is assumed to be predefined and we require an expression for proper time as a function of coordinate time. From the experimental point of view, proper time is what is measured experimentally and then coordinate time is calculated from the proper time of some inertial clocks.
\int \sqrt {1 - \frac{1}{c^2} \left [ \left (\frac{dx}{dt}\right)^2 + \left (\frac{dy}{dt}\right)^2 + \left ( \frac{dz}{dt}\right)^2 \right] } \,dt,
where is the coordinate speed at coordinate time , and , , and are Cartesian spatial
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
coordinates.
If , , , and are all parameterised by a parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
, this can be written as
In differential form it can be written as the line integral
where is the path of the clock in spacetime.
To make things even easier, inertial motion
Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
in special relativity is where the spatial coordinates change at a constant rate with respect to the temporal coordinate. This further simplifies the proper time equation to
where Δ means "the change in" between two events.
The special relativity equations are special cases of the general case that follows.
In general relativity
Using tensor calculus, proper time is more rigorously defined in general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
as follows: Given a spacetime which is a pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
mapped with a coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
 and equipped with a corresponding metric tensor
and equipped with a corresponding metric tensorMetric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
 , the proper time
, the proper time  experienced in moving between two events along a timelike path P is given by the line integral
experienced in moving between two events along a timelike path P is given by the line integralLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
where
(Note: the Einstein summation convention is used in the above. The expression AμBμ is shorthand for , and the μ in Bμ denotes an index, not a power.)
Derivation
For any spacetime, there is an incremental invariant interval ds between events with an incremental coordinate separation dxμ ofThis is referred to as the line element of the spacetime. s may be spacelike, lightlike, or timelike. Spacelike paths cannot be physically traveled (as they require moving faster than light). Lightlike paths can only be followed by light beams, for which there is no passage of proper time. Only timelike paths can be traveled by massive objects, in which case the invariant interval becomes the proper time
 . So for our purposes
. So for our purposes  .
.Taking the square root of each side of the line element gives the above definition of
 . After that, take the line integral of each side to get
. After that, take the line integral of each side to get  as described by the first equation.
as described by the first equation.Derivation for special relativity
In special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
spacetime is mapped with a four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
coordinate system
 where
where
- t is a temporalTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
coordinate and - x, y, and z are orthogonal spatialSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
coordinates.
This spacetime and mapping are described with the Minkowski metric:
-

(Note: The +--- metric signatureMetric signatureThe signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
is used in this article so that will always be positivePositivePositive is a property of positivity and may refer to:- Mathematics and science :* Converging lens or positive lens, in optics* Plus sign, the sign "+" used to indicate a positive number* Positive , a polarity of electrical charge...
will always be positivePositivePositive is a property of positivity and may refer to:- Mathematics and science :* Converging lens or positive lens, in optics* Plus sign, the sign "+" used to indicate a positive number* Positive , a polarity of electrical charge...
definite for timelike paths.)
In special relativity, the proper time equation becomes
as above.
Example 1: The twin "paradox"
For a twin "paradox"Twin paradoxIn physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...
scenario, let there be an observer A who moves between the coordinates (0,0,0,0) and (10 years, 0, 0, 0) inertially. This means that A stays at for 10 years of coordinate time. The proper time for A is then
for 10 years of coordinate time. The proper time for A is then
So we find that being "at rest" in a special relativity coordinate system means that proper time and coordinate time are the same.
Let there now be another observer B who travels in the x direction from (0,0,0,0) for 5 years of coordinate time at 0.866c to (5 years, 4.33 light-years, 0, 0). Once there, B accelerates, and travels in the other spatial direction for 5 years to (10 years, 0, 0, 0). For each leg of the trip, the proper time is
So the total proper time for observer B to go from (0,0,0,0) to (5 years, 4.33 light-years, 0, 0) to (10 years, 0, 0, 0) is 5 years. Thus it is shown that the proper time equation incorporates the time dilation effect. In fact, for an object in a SR spacetime traveling with a velocity of v for a time , the proper time experienced is
, the proper time experienced is
which is the SR time dilation formula.
Example 2: The rotating disk
An observer rotating around another inertial observer is in an accelerated frame of reference. For such an observer, the incremental ( ) form of the proper time equation is needed, along with a parameterized description of the path being taken, as shown below.
) form of the proper time equation is needed, along with a parameterized description of the path being taken, as shown below.
Let there be an observer C on a disk rotating in the xy plane at a coordinate angular rate of and who is at a distance of r from the center of the disk with the center of the disk at x=y=z=0. The path of observer C is given by
and who is at a distance of r from the center of the disk with the center of the disk at x=y=z=0. The path of observer C is given by  , where
, where  is the current coordinate time. When r and
is the current coordinate time. When r and  are constant,
are constant,  and
and  . The incremental proper time formula then becomes
. The incremental proper time formula then becomes
So for an observer rotating at a constant distance of r from a given point in spacetime at a constant angular rate of ω between coordinate times and
and  , the proper time experienced will be
, the proper time experienced will be
As v=rω for a rotating observer, this result is as expected given the time dilation formula above, and shows the general application of the integral form of the proper time formula.
Examples in general relativity
The difference between SR and general relativity (GR) is that in GR you can use any metric which is a solution of the Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
, not just the Minkowski metric. Because inertial motion in curved spacetimes lacks the simple expression it has in SR, the line integral form of the proper time equation must always be used.
Example 3: The rotating disk (again)
An appropriate coordinate conversion done against the Minkowski metric creates coordinates where an object on a rotating disk stays in the same spatial coordinate position. The new coordinates are
and
The t and z coordinates remain unchanged. In this new coordinate system, the incremental proper time equation is
With r, θ, and z being constant over time, this simplifies to
which is the same as in Example 2.
Now let there be an object off of the rotating disk and at inertial rest with respect to the center of the disk and at a distance of R from it. This object has a coordinate motion described by dθ = -ω dt, which describes the inertially at-rest object of counter-rotating in the view of the rotating observer. Now the proper time equation becomes
So for the inertial at-rest observer, coordinate time and proper time are once again found to pass at the same rate, as expected and required for the internal self-consistency of relativity theory.
Example 4: The Schwarzschild solution — time on the Earth
The Schwarzschild solution has an incremental proper time equation of
where- t is time as calibrated with a clock distant from and at inertial rest with respect to the Earth,
- r is a radial coordinate (which is effectively the distance from the Earth's center),
- θ is the latitudinal coordinate, being the angular separation from the north poleNorth PoleThe North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
in radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. -
 is a longitudinal coordinate, analogous to the latitude on the Earth's surface but independent of the Earth's rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
is a longitudinal coordinate, analogous to the latitude on the Earth's surface but independent of the Earth's rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. This is also given in radians. - m is the geometrized mass of a central massive object, being m = MG/c2,
- M is the mass of the object,
- G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
.
To demonstrate the use of the proper time relationship, several sub-examples involving the Earth will be used here. The use of the Schwarzschild solution for the Earth is not entirely correct for the following reasons:- Due to its rotation, the Earth is an oblate spheroid instead of being a true sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. This results in the gravitational field also being oblate instead of spherical. - In GR, a rotating object also drags spacetime along with itself. This is described by the Kerr solution. However, the amount of frame dragging that occurs for the Earth is so small that it can be ignored.
For the EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, M = 5.9742 × 1024 kg, meaning that m = 4.4354 × 10 −3 m. When standing on the north pole, we can assume (meaning that we are neither moving up or down or along the surface of the Earth). In this case, the Schwarzschild solution proper time equation becomes
(meaning that we are neither moving up or down or along the surface of the Earth). In this case, the Schwarzschild solution proper time equation becomes  . Then using the polar radius of the Earth as the radial coordinate (or
. Then using the polar radius of the Earth as the radial coordinate (or  meters), we find that
meters), we find that
At the equatorEquatorAn equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
, the radius of the Earth is r = 6,378,137 meters. In addition, the rotation of the Earth needs to be taken into account. This imparts on an observer an angular velocity of of 2π divided by the sidereal periodSidereal timeSidereal time is a time-keeping system astronomers use to keep track of the direction to point their telescopes to view a given star in the night sky...
of 2π divided by the sidereal periodSidereal timeSidereal time is a time-keeping system astronomers use to keep track of the direction to point their telescopes to view a given star in the night sky...
of the Earth's rotation, 86162.4 seconds. So . The proper time equation then produces
. The proper time equation then produces
This should have been the same as the previous result, but as noted above the Earth is not spherical as assumed by the Schwarzschild solution. Even so this demonstrates how the proper time equation is used.
See also
- Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
- Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
- Proper lengthProper lengthIn relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime....
- Proper accelerationProper accelerationIn relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
- Proper massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
- Proper velocityProper velocityIn relativity, proper-velocity, also known as celerity, is an alternative to velocity for measuring motion. Whereas velocity relative to an observer is distance per unit time where both distance and time are measured by the observer, proper velocity relative to an observer divides observer-measured...
- Clock hypothesisClock hypothesisThe clock hypothesis is an assumption in special relativity. It states that the rate of a clock doesn't depend on its acceleration but only on its instantaneous velocity...
Footnotes
-





















