
Maxwell stress tensor
Encyclopedia
The Maxwell Stress Tensor (named after James Clerk Maxwell
) is a mathematical object in physics
, more precisely it is a second rank tensor
used in classical electromagnetism
to represent the interaction between electric/magnetic forces and mechanical momentum
. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impossibly difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
If we start out with the Lorentz force law, and write down the force per unit volume for an unknown charge distribution, the motivation for the Maxwell stress tensor becomes apparent.
This is the differential form of the Lorentz force law, the usual can be obtained by integrating over the volume. If we now use Maxwell's equations
can be obtained by integrating over the volume. If we now use Maxwell's equations
we can replace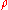 and
and 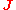 so that only the fields
so that only the fields  and
and  are used:
are used: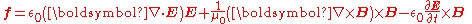
where we have used Gauss' law
and Ampère's law. Now, using the product rule
, we can rewrite the time derivative to something that can be interpreted physically, namely the Poynting vector
. We observe that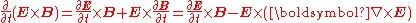
where we have used Faradays law, and we can now rewrite as
as ,
,
or collecting terms with and
and  we have
we have .
.
Notice that a term seems to be "missing" from the symmetry. We can, however, add this term to achieve symmetry since Gauss' law for magnetism tells us that . This leaves us with
. This leaves us with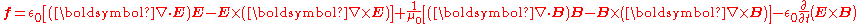 .
.
This would be relatively straightforward to calculate if we only could get rid of those curls, which are more demanding. Fortunately we have the curl identity,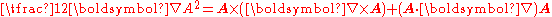 ,
,
so we end up with .
.
This expression contains every aspect of electromagnetism and momentum and is relatively easy to compute. It can be written more compactly by introducing the Maxwell stress tensor,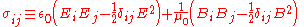 ,
,
and notice that all but the last term of the above can be written as the divergence of this: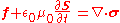 ,
,
where we have finally introduced the Poynting vector
,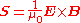 .
.
, the Maxwell stress tensor is the stress tensor
of an electromagnetic field
. As derived above in SI units, it is given by: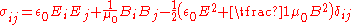 ,
,
where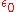 is the electric constant
is the electric constant
and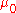 is the magnetic constant,
is the magnetic constant,  is the electric field
is the electric field
, is the magnetic field
is the magnetic field
and is Kronecker's delta. In Gaussian (CGS) units, more commonly used in physics textbooks, it is given by:
is Kronecker's delta. In Gaussian (CGS) units, more commonly used in physics textbooks, it is given by: ,
,
where is the magnetizing field.
is the magnetizing field.
An alternative way of expressing this tensor is: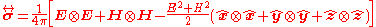 ,
,
where is the dyadic product.
is the dyadic product.
The element ij of the Maxwell stress tensor has units of momentum per unit of area times time and gives the flux of momentum parallel to the ith axis crossing a surface normal to the jth axis (in the negative direction) per unit of time.
These units can also be seen as units of force per unit of area (negative pressure), and the ij element of the tensor can also be interpreted as the force parallel to the ith axis suffered by a surface normal to the jth axis per unit of area. Indeed the diagonal elements give the tension (pulling) acting on a differential area element normal to the corresponding axis. Unlike forces due to the pressure of an ideal gas, an area element in the electromagnetic field also feels a force in a direction that is not normal to the element. This shear is given by the off-diagonal elements of the stress tensor.
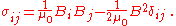
For cylindrical objects, such as the rotor of a motor, this is further simplified to: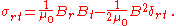
Where r is the shear in the radial (outward from the cylinder) direction, and t is the shear in the tangential (around the cylinder) direction. It is the tangential force which spins the motor. Br is the flux density in the radial direction, and Bt is the flux density in the tangential direction.
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
) is a mathematical object in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, more precisely it is a second rank tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
used in classical electromagnetism
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
to represent the interaction between electric/magnetic forces and mechanical momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impossibly difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
Motivation
| Name | Differential form |
|---|---|
| Gauss's law (in vacuum) | 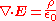 |
| Gauss's law for magnetism |  |
| Maxwell–Faraday equation (Faraday's law of induction) |
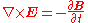 |
| Ampère's circuital law (in vacuum) (with Maxwell's correction) |
 |
If we start out with the Lorentz force law, and write down the force per unit volume for an unknown charge distribution, the motivation for the Maxwell stress tensor becomes apparent.

This is the differential form of the Lorentz force law, the usual
 can be obtained by integrating over the volume. If we now use Maxwell's equations
can be obtained by integrating over the volume. If we now use Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
we can replace
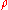 and
and 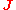 so that only the fields
so that only the fields  and
and  are used:
are used: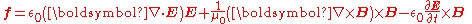
where we have used Gauss' law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and Ampère's law. Now, using the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, we can rewrite the time derivative to something that can be interpreted physically, namely the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
. We observe that
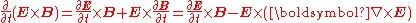
where we have used Faradays law, and we can now rewrite
 as
as ,
,or collecting terms with
 and
and  we have
we have .
.Notice that a term seems to be "missing" from the symmetry. We can, however, add this term to achieve symmetry since Gauss' law for magnetism tells us that
 . This leaves us with
. This leaves us with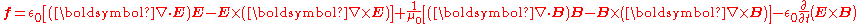 .
.This would be relatively straightforward to calculate if we only could get rid of those curls, which are more demanding. Fortunately we have the curl identity,
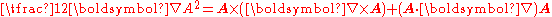 ,
,so we end up with
 .
.This expression contains every aspect of electromagnetism and momentum and is relatively easy to compute. It can be written more compactly by introducing the Maxwell stress tensor,
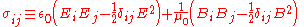 ,
,and notice that all but the last term of the above can be written as the divergence of this:
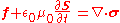 ,
,where we have finally introduced the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
,
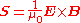 .
.Equation
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Maxwell stress tensor is the stress tensor
Stress tensor
Stress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...
of an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. As derived above in SI units, it is given by:
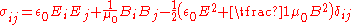 ,
,where
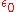 is the electric constant
is the electric constantElectric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
and
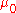 is the magnetic constant,
is the magnetic constant,  is the electric field
is the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
,
 is the magnetic field
is the magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and
 is Kronecker's delta. In Gaussian (CGS) units, more commonly used in physics textbooks, it is given by:
is Kronecker's delta. In Gaussian (CGS) units, more commonly used in physics textbooks, it is given by: ,
,where
 is the magnetizing field.
is the magnetizing field.An alternative way of expressing this tensor is:
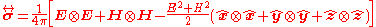 ,
,where
 is the dyadic product.
is the dyadic product.The element ij of the Maxwell stress tensor has units of momentum per unit of area times time and gives the flux of momentum parallel to the ith axis crossing a surface normal to the jth axis (in the negative direction) per unit of time.
These units can also be seen as units of force per unit of area (negative pressure), and the ij element of the tensor can also be interpreted as the force parallel to the ith axis suffered by a surface normal to the jth axis per unit of area. Indeed the diagonal elements give the tension (pulling) acting on a differential area element normal to the corresponding axis. Unlike forces due to the pressure of an ideal gas, an area element in the electromagnetic field also feels a force in a direction that is not normal to the element. This shear is given by the off-diagonal elements of the stress tensor.
Magnetism only
If the field is only magnetic (which is largely true in motors, for instance), some of the terms drop out, and the equation in SI units becomes: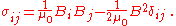
For cylindrical objects, such as the rotor of a motor, this is further simplified to:
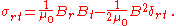
Where r is the shear in the radial (outward from the cylinder) direction, and t is the shear in the tangential (around the cylinder) direction. It is the tangential force which spins the motor. Br is the flux density in the radial direction, and Bt is the flux density in the tangential direction.
See also
- Energy density of electric and magnetic fields
- Poynting vectorPoynting vectorIn physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
- Electromagnetic stress-energy tensor

