Rapidity
Encyclopedia
In relativity
, rapidity is an alternative to speed
as a framework for measuring motion. On parallel
velocities (say, in one-dimensional space) rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The rapidity of light is infinite. Rapidity can also link geometric techniques to Minkowski diagrams
. The rapidity concept is not widely (nor fashionably) used; speed has the advantage of more direct measurability.
is the hyperbolic angle
defined as
where
For low speeds, φ is approximately v/c.
In 1910 E.T. Whittaker used this parameter in his description of the development of the Lorentz transformation in the first edition of his History of the Theories of Aether and Electricity.
The rapidity parameter was named in 1911 by Alfred Robb
; his term was acknowledged by Varićak
(1912), Silberstein (1914), Eddington (1924), Morley (1936) and Rindler (2001).
.
The matrix Λ(φ) is of the type
with p and q satisfying 
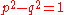. The study of all matrices 
with p, q ∈ R is taken up in the article split-complex number
. It is not hard to prove that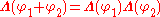
.
This establishes the useful additive property of rapidity: if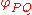
denotes the rapidity of Q relative to P, then
,
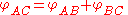provided A, B and C all lie on the same straight line. The simplicity of this formula contrasts with the complexity of the corresponding velocity-addition formula. The simple formula (as well as the matrix above) is analogous to a formula for adding angles of two ordinary rotations in the Euclidean space (and for a rotation matrix): indeed, rapidity may be understood as a "hyperbolic angle" or a Minkowskian counterpart of an angle.
The exponential function, logarithm, sinh, cosh, and tanh are all transcendental function
s, requiring methods beyond algebraic expression. Conservatism in physical science explains the reluctance to rely on these functions in some presentations of relativity physics (see Scott Walter (1999)). Nevertheless, the Lorentz factor
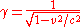
identifies with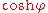
where φ is rapidity. So the hyperbolic angle φ is implicit in the Lorentz transformation
expressions using γ and β.
Mathematically, the rapidity can be viewed as a re-linearization of the speed, since the naively linear v becomes absurd as v approaches c.
Proper acceleration
(the acceleration 'felt' by the object being accelerated) is the rate of change of rapidity with respect to proper time
(time as measured by the object undergoing acceleration itself). Therefore the rapidity of an object in a given frame can be viewed simply as the velocity of that object as would be calculated non-relativistically by an inertial guidance system on board the object itself if it accelerated from rest in that frame to its given speed.
corresponds to the proper acceleration (see above). This is a non-flat space (namely, a hyperbolic space
), and rapidity is just the distance
from the given velocity to the zero velocity in given frame of reference. Although it is possible, as noted above, to add and subtract rapidities where corresponding relative velocities are parallel, in general case the rapidity-addition formula is more complex because of negative curvature
. For example, the result of "addition" of two perpendicular motions with rapidities φ1 and φ2 will be greater than
expected by Pythagorean theorem
. Rapidity in two dimensions can be usefully visualized using the Poincare disk. Points at the edge of the disk correspond to infinite rapidity. Geodesics correspond to steady accelerations. The Thomas precession
is equal to minus the angular deficit of a triangle, or to minus the area of the triangle.
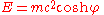
and so rapidity can be calculated from measured energy and momentum by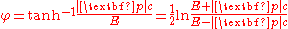
However, experimental particle physicists often use a modified definition of rapidity relative to a beam axis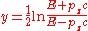
where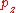
is the component of momentum along the beam axis. This is the rapidity of the boost along the beam axis which takes an observer from the lab frame to a frame in which the particle moves only perpendicular to the beam. Related to this is the concept of pseudorapidity.
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, rapidity is an alternative to speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
as a framework for measuring motion. On parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
velocities (say, in one-dimensional space) rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The rapidity of light is infinite. Rapidity can also link geometric techniques to Minkowski diagrams
Minkowski diagram
The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...
. The rapidity concept is not widely (nor fashionably) used; speed has the advantage of more direct measurability.
Detail
The rapidity φ of an object relative to a frame of referenceFrame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
is the hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
defined as
where
- v is the speedSpeedIn kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
of the object relative to the same frame of reference, - c is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, and - tanh−1 is the inverse hyperbolic tangent functionInverse hyperbolic functionThe inverses of the hyperbolic functions are the area hyperbolic functions. The names hint at the fact that they give the area of a sector of the unit hyperbola in the same way that the inverse trigonometric functions give the arc length of a sector on the unit circle...
.
For low speeds, φ is approximately v/c.
In 1910 E.T. Whittaker used this parameter in his description of the development of the Lorentz transformation in the first edition of his History of the Theories of Aether and Electricity.
The rapidity parameter was named in 1911 by Alfred Robb
Alfred Robb
Alfred Arthur Robb or Alfred A. Robb FRS was a British physicist.Robb studied at Queen's College in Belfast and at St John’s College in Cambridge. He then proceeded to University of Göttingen, where guided by Woldemar Voigt, he wrote his dissertation on the Zeeman effect. He also worked under J. J...
; his term was acknowledged by Varićak
Vladimir Varicak
Vladimir Varićak was a Croatian mathematician and theoretical physicist of Serbian descent....
(1912), Silberstein (1914), Eddington (1924), Morley (1936) and Rindler (2001).
In one spatial dimension
The rapidity φ arises in the linear representation of a Lorentz boost as a vector-matrix product.The matrix Λ(φ) is of the type
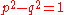with p and q satisfying . The study of all matrices with p, q ∈ R is taken up in the article split-complex numberSplit-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
. It is not hard to prove that
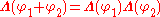.This establishes the useful additive property of rapidity: if
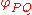denotes the rapidity of Q relative to P, then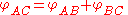,provided A, B and C all lie on the same straight line. The simplicity of this formula contrasts with the complexity of the corresponding velocity-addition formula. The simple formula (as well as the matrix above) is analogous to a formula for adding angles of two ordinary rotations in the Euclidean space (and for a rotation matrix): indeed, rapidity may be understood as a "hyperbolic angle" or a Minkowskian counterpart of an angle.
The exponential function, logarithm, sinh, cosh, and tanh are all transcendental function
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s, requiring methods beyond algebraic expression. Conservatism in physical science explains the reluctance to rely on these functions in some presentations of relativity physics (see Scott Walter (1999)). Nevertheless, the Lorentz factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
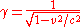
identifies with
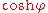where φ is rapidity. So the hyperbolic angle φ is implicit in the Lorentz transformationLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
expressions using γ and β.
Mathematically, the rapidity can be viewed as a re-linearization of the speed, since the naively linear v becomes absurd as v approaches c.
Proper acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
(the acceleration 'felt' by the object being accelerated) is the rate of change of rapidity with respect to proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
(time as measured by the object undergoing acceleration itself). Therefore the rapidity of an object in a given frame can be viewed simply as the velocity of that object as would be calculated non-relativistically by an inertial guidance system on board the object itself if it accelerated from rest in that frame to its given speed.
In more than one spatial dimension
From mathematical point of view, possible values of relativistic velocity form a manifold, where the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
corresponds to the proper acceleration (see above). This is a non-flat space (namely, a hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
), and rapidity is just the distance
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
from the given velocity to the zero velocity in given frame of reference. Although it is possible, as noted above, to add and subtract rapidities where corresponding relative velocities are parallel, in general case the rapidity-addition formula is more complex because of negative curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
. For example, the result of "addition" of two perpendicular motions with rapidities φ1 and φ2 will be greater than
expected by Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. Rapidity in two dimensions can be usefully visualized using the Poincare disk. Points at the edge of the disk correspond to infinite rapidity. Geodesics correspond to steady accelerations. The Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
is equal to minus the angular deficit of a triangle, or to minus the area of the triangle.
In experimental particle physics
The energy E and scalar momentum |p| of a particle of non-zero (rest) mass m are given by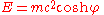and so rapidity can be calculated from measured energy and momentum by
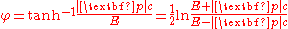
However, experimental particle physicists often use a modified definition of rapidity relative to a beam axis
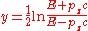
where
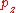is the component of momentum along the beam axis. This is the rapidity of the boost along the beam axis which takes an observer from the lab frame to a frame in which the particle moves only perpendicular to the beam. Related to this is the concept of pseudorapidity.