
Algebra of physical space
Encyclopedia
In physics
, the algebra of physical space (APS) is the use of the Clifford
or geometric algebra
Cℓ3 of the three-dimensional Euclidean space
as a model for (3+1)-dimensional space-time, representing a point in space-time via a paravector
(3-dimensional vector plus a 1-dimensional scalar).
The Clifford algebra Cℓ3 has a faithful representation
, generated by Pauli matrices
, on the spin representation C2; further, Cℓ3 is isomorphic to the even subalgebra of the 3+1 Clifford algebra, Cℓ.
APS can be used to construct a compact, unified and geometrical formalism for both classical and quantum mechanics.
APS should not be confused with spacetime algebra
(STA), which concerns the Clifford algebra
Cℓ1,3(R) of the four dimensional Minkowski spacetime.
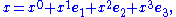
where the time is given by the scalar part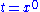 with
with  . In the Pauli matrix representation the unit basis vectors are replaced by
. In the Pauli matrix representation the unit basis vectors are replaced by
the Pauli matrices and the scalar part by the identity matrix. This means that the Pauli
matrix representation of the space-time position is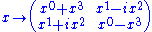
The four-velocity
also called proper velocity is paravector defined as the proper time
derivative of the space-time position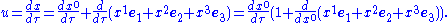
This expression can be brought to a more compact form by defining the ordinary velocity as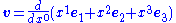
and recalling the definition of the gamma factor
, so that the proper velocity becomes
The proper velocity is a positive unimodular
paravector, which implies the following condition in terms of the Clifford conjugation
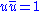
The proper velocity transforms under the action of the Lorentz rotor
 as
as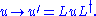
The restricted Lorentz transformations that preserve the direction of time and include rotations and boosts can be performed by an exponentiation of the
space-time rotation biparavector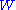
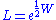
In the matrix representation the Lorentz rotor is seen to form an instance
of the SL(2,C) group, which is the double cover of the Lorentz group
.
The unimodularity of the Lorentz rotor is translated in the following condition
in terms of the product of the Lorentz rotor with its Clifford conjugation
This Lorentz rotor can be always decomposed in two factors, one Hermitian
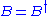 , and the other unitary
, and the other unitary
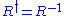 , such that
, such that
The unitary element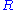 is called rotor because encodes rotations
is called rotor because encodes rotations
and the Hermitian element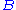 is called boost.
is called boost.
The four-momentum
in APS can be obtained by multiplying the
proper velocity with the mass as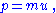
with the mass shell condition translated into
is represented as a bi-paravector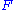 ,
,
with the Hermitian part representing the Electric field and the
anti-Hermitian part representing the magnetic field. In the standard Pauli matrix
representation, the electromagnetic field is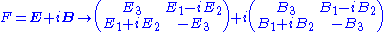
The electromagnetic field is obtained from the paravector
potential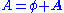 as
as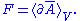
and the electromagnetic field is invariant under a gauge transformation of the form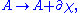
where is a scalar function.
is a scalar function.
The Electromagnetic field is covariant
under Lorentz transformations according to the law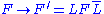
The Maxwell equations
can be expressed in a single equation as follows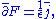
where the overbar represents the Clifford conjugation and
the four-current
is defined as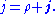
The electromagnetic Lagrangian is
which is evidently a real scalar invariant.
The Lorentz force
equation takes the form
 ,
,
where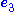 is an arbitrary unitary vector and
is an arbitrary unitary vector and  is the
is the
paravector potential that includes the vector potential
and the electric potential
.
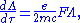
such that the proper velocity is calculated as the Lorentz transformation of the proper
velocity at rest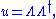
which can be integrated to find the space-time trajectory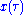 with the additional use of
with the additional use of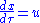
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the algebra of physical space (APS) is the use of the Clifford
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
or geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
Cℓ3 of the three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
as a model for (3+1)-dimensional space-time, representing a point in space-time via a paravector
Paravector
The name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
(3-dimensional vector plus a 1-dimensional scalar).
The Clifford algebra Cℓ3 has a faithful representation
Faithful representation
In mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
, generated by Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
, on the spin representation C2; further, Cℓ3 is isomorphic to the even subalgebra of the 3+1 Clifford algebra, Cℓ.
APS can be used to construct a compact, unified and geometrical formalism for both classical and quantum mechanics.
APS should not be confused with spacetime algebra
Spacetime algebra
In mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
(STA), which concerns the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ1,3(R) of the four dimensional Minkowski spacetime.
Special Relativity
In APS, the space-time position is represented as a paravectorParavector
The name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
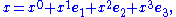
where the time is given by the scalar part
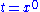 with
with  . In the Pauli matrix representation the unit basis vectors are replaced by
. In the Pauli matrix representation the unit basis vectors are replaced bythe Pauli matrices and the scalar part by the identity matrix. This means that the Pauli
matrix representation of the space-time position is
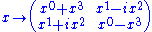
The four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
also called proper velocity is paravector defined as the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
derivative of the space-time position
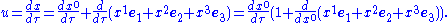
This expression can be brought to a more compact form by defining the ordinary velocity as
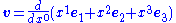
and recalling the definition of the gamma factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
, so that the proper velocity becomes

The proper velocity is a positive unimodular
Unimodular matrix
In mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
paravector, which implies the following condition in terms of the Clifford conjugation
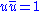
The proper velocity transforms under the action of the Lorentz rotor
 as
as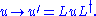
The restricted Lorentz transformations that preserve the direction of time and include rotations and boosts can be performed by an exponentiation of the
space-time rotation biparavector
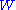
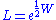
In the matrix representation the Lorentz rotor is seen to form an instance
of the SL(2,C) group, which is the double cover of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
The unimodularity of the Lorentz rotor is translated in the following condition
in terms of the product of the Lorentz rotor with its Clifford conjugation

This Lorentz rotor can be always decomposed in two factors, one Hermitian
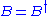 , and the other unitary
, and the other unitary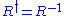 , such that
, such that
The unitary element
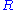 is called rotor because encodes rotations
is called rotor because encodes rotationsand the Hermitian element
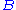 is called boost.
is called boost.The four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
in APS can be obtained by multiplying the
proper velocity with the mass as
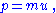
with the mass shell condition translated into

Classical Electrodynamics
The electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
is represented as a bi-paravector
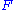 ,
,with the Hermitian part representing the Electric field and the
anti-Hermitian part representing the magnetic field. In the standard Pauli matrix
representation, the electromagnetic field is
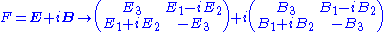
The electromagnetic field is obtained from the paravector
Paravector
The name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
potential
 as
as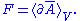
and the electromagnetic field is invariant under a gauge transformation of the form
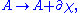
where
 is a scalar function.
is a scalar function.The Electromagnetic field is covariant
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
under Lorentz transformations according to the law
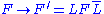
The Maxwell equations
can be expressed in a single equation as follows
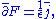
where the overbar represents the Clifford conjugation and
the four-current
Four-current
In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
is defined as
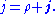
The electromagnetic Lagrangian is

which is evidently a real scalar invariant.
The Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
equation takes the form

Relativistic Quantum Mechanics
The Dirac equation takes the form ,
,where
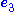 is an arbitrary unitary vector and
is an arbitrary unitary vector and  is the
is theparavector potential that includes the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
and the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
.
Classical Spinor
The differential equation of the Lorentz rotor that is consistent with the Lorentz force is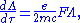
such that the proper velocity is calculated as the Lorentz transformation of the proper
velocity at rest
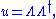
which can be integrated to find the space-time trajectory
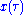 with the additional use of
with the additional use of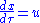
See also
- ParavectorParavectorThe name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
- MultivectorMultivectorIn multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
- wikibooks:Physics in the Language of Geometric Algebra. An Approach with the Algebra of Physical Space
- Dirac equation in the algebra of physical spaceDirac equation in the algebra of physical spaceThe Dirac equation, as the relativistic equation that describesspin 1/2 particles in quantum mechanics can be written in terms of the Algebra of physical space , which is a case of a Clifford algebra or geometric algebrathat is based in the use of paravectors....
Textbooks
- Baylis, William (2002). Electrodynamics: A Modern Geometric Approach (2nd ed.). Birkhäuser. ISBN 0-8176-4025-8
- W. E. Baylis, editor, Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering, Birkhäuser, Boston 1996.
- Chris Doran and Anthony Lasenby, Geometric Algebra for Physicists, Cambridge University Press (2003)
- David HestenesDavid HestenesDavid Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
: New Foundations for Classical Mechanics (Second Edition). ISBN 0-7923-5514-8, Kluwer Academic Publishers (1999)
Articles
- Baylis, William (2002). Relativity in Introductory Physics, Can. J. Phys. 82 (11), 853—873 (2004). (ArXiv:physics/0406158)
- W. E. Baylis and G. Jones, The Pauli-Algebra Approach to Special Relativity, J. Phys. A22, 1-16 (1989)
- W. E. Baylis, Classical eigenspinors and the Dirac equation ,Phys Rev. A, Vol 45, number 7 (1992)
- W. E. Baylis, Relativistic dynamics of charges in electromagnetic fields: An eigenspinor approach ,Phys Rev. A, Vol 60, number 2 (1999)

