Universal covering group
Encyclopedia
In mathematics
, a covering group of a topological group
H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism
. The map p is called the covering homomorphism. A frequently occurring case is a double covering group, a topological double cover in which H has index
2 in G; examples include the Spin groups, Pin group
s, and metaplectic group
s.
normal subgroup
of G. The kernel K is closed
in G if and only if G is Hausdorff
(and if and only if H is Hausdorff). Going in the other direction, if G is any topological group and K is a discrete normal subgroup of G then the quotient map p : G → G/K is a covering homomorphism.
If G is connected
then K, being a discrete normal subgroup, necessarily lies in the center
of G and is therefore abelian
. In this case, the center of H = G/K is given by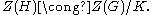
As with all covering spaces, the fundamental group
of G injects into the fundamental group of H. If G is path-connected then the quotient group
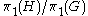is isomorphic to K. Since the fundamental group of a topological group is always abelian, every covering group is a normal covering space. The group K acts
simply transitively on the fibers (which are just left coset
s) by right multiplication. The group G is then a principal K-bundle
over H.
If G is a covering group of H then the groups G and H are locally isomorphic. Moreover, given any two connected locally isomorphic groups H1 and H2, there exists a topological group G with discrete normal subgroups K1 and K2 such that H1 is isomorphic to G/K1 and H2 is isomorphic to G/K2.
The construction is as follows. Let a and b be elements of G and let f and g be path
s in G starting at e* and terminating at a and b respectively. Define a path h : I → H by h(t) = p(f(t))p(g(t)). By the path-lifting property of covering spaces there is a unique lift of h to G with initial point e*. The product ab is defined as the endpoint of this path. By construction we have p(ab) = p(a)p(b). One must show that this definition is independent of the choice of paths f and g, and also that the group operations are continuous.
Let PH be the path group of H. That is, PH is the space of path
s in H based at the identity together with the compact-open topology
. The product of paths is given by pointwise multiplication, i.e. (fg)(t) = f(t)g(t). This gives PH the structure of a topological group. There is a natural group homomorphism PH → H which sends each path to its endpoint. The universal cover of H is given as the quotient of PH by the normal subgroup of null-homotopic loop
s. The projection PH → H descends to the quotient giving the covering map. One can show that the universal cover is simply connected and the kernel is just the fundamental group
of H. That is, we have a short exact sequence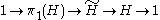
where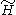
is the universal cover of H. Concretely, the universal covering group of H is the space of homotopy classes of paths in H with pointwise multiplication of paths. The covering map sends each path class to its endpoint.
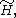while the minimal element is the universal covering group mod its center, 
.
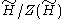This corresponds algebraically to the universal perfect central extension (called "covering group", by analogy) as the maximal element, and a group mod its center as minimal element.
This is particularly important for Lie groups, as these groups are all the (connected) realizations of a particular Lie algebra. For many Lie groups the center is the group of scalar matrices, and thus the group mod its center is the projectivization of the Lie group. These covers are important in studying projective representation
s of Lie groups, and spin representations lead to the discovery of spin groups: a projective representation of a Lie group need not come from a linear representation of the group, but does come from a linear representation of some covering group, in particular the universal covering group. The finite analog led to the covering group or Schur cover, as discussed above.
A key example arises from SL2(R), which has center {±1} and fundamental group Z. It is a double cover of the centerless projective special linear group PSL2(R), which is obtained by taking the quotient by the center. By Iwasawa decomposition
, both groups are circle bundles over the complex upper half-plane, and their universal cover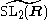
is a real line bundle over the half-plane that forms one of Thurston's eight geometries
. Since the half-plane is contractible, all bundle structures are trivial. The preimage of SL2(Z) in the universal cover is isomorphic to the braid group
on three strands.
s. In particular, every covering of a manifold
is a manifold, and the covering homomorphism becomes a smooth map. Likewise, given any discrete normal subgroup of a Lie group the quotient group is a Lie group and the quotient map is a covering homomorphism.
Two Lie groups are locally isomorphic if and only if the their Lie algebras are isomorphic. This implies that a homomorphism φ : G → H of Lie groups is a covering homomorphism if and only if the induced map on Lie algebras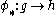
is an isomorphism.
Since for every Lie algebra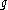
there is a unique simply connected Lie group G with Lie algebra 
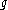, from this follows that the universal convering group of a connected Lie group H is the (unique) simply connected Lie group G having the same Lie algebra as H.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a covering group of a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
. The map p is called the covering homomorphism. A frequently occurring case is a double covering group, a topological double cover in which H has index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 in G; examples include the Spin groups, Pin group
Pin group
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s, and metaplectic group
Metaplectic group
In mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
s.
Properties
Let G be a covering group of H. The kernel K of the covering homomorphism is just the fiber over the identity in H and is a discreteDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G. The kernel K is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in G if and only if G is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(and if and only if H is Hausdorff). Going in the other direction, if G is any topological group and K is a discrete normal subgroup of G then the quotient map p : G → G/K is a covering homomorphism.
If G is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
then K, being a discrete normal subgroup, necessarily lies in the center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of G and is therefore abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. In this case, the center of H = G/K is given by
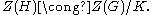
As with all covering spaces, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of G injects into the fundamental group of H. If G is path-connected then the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
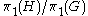is isomorphic to K. Since the fundamental group of a topological group is always abelian, every covering group is a normal covering space. The group K actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
simply transitively on the fibers (which are just left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s) by right multiplication. The group G is then a principal K-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over H.
If G is a covering group of H then the groups G and H are locally isomorphic. Moreover, given any two connected locally isomorphic groups H1 and H2, there exists a topological group G with discrete normal subgroups K1 and K2 such that H1 is isomorphic to G/K1 and H2 is isomorphic to G/K2.
Group structure on a covering space
Let H be a topological group and let G be a covering space of H. If G and H are both path-connected and locally path-connected, then for any choice of element e* in the fiber over e ∈ H, there exists a unique topological group structure on G, with e* as the identity, for which the covering map p : G → H is a homomorphism.The construction is as follows. Let a and b be elements of G and let f and g be path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
s in G starting at e* and terminating at a and b respectively. Define a path h : I → H by h(t) = p(f(t))p(g(t)). By the path-lifting property of covering spaces there is a unique lift of h to G with initial point e*. The product ab is defined as the endpoint of this path. By construction we have p(ab) = p(a)p(b). One must show that this definition is independent of the choice of paths f and g, and also that the group operations are continuous.
Universal covering group
If H is a path-connected, locally path-connected, and semilocally simply connected group then it has a universal cover. By the previous construction the universal cover can be made into a topological group with the covering map a continuous homomorphism. This group is called the universal covering group of H. There is also a more direct construction which we give below.Let PH be the path group of H. That is, PH is the space of path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
s in H based at the identity together with the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
. The product of paths is given by pointwise multiplication, i.e. (fg)(t) = f(t)g(t). This gives PH the structure of a topological group. There is a natural group homomorphism PH → H which sends each path to its endpoint. The universal cover of H is given as the quotient of PH by the normal subgroup of null-homotopic loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
s. The projection PH → H descends to the quotient giving the covering map. One can show that the universal cover is simply connected and the kernel is just the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of H. That is, we have a short exact sequence
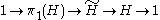
where
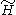is the universal cover of H. Concretely, the universal covering group of H is the space of homotopy classes of paths in H with pointwise multiplication of paths. The covering map sends each path class to its endpoint.Lattice of covering groups
As the above suggest, if a group has a universal covering group (if it is path-connected, locally path-connected, and semilocally simply connected), with discrete center, then the set of all topologically groups that are covered by the universal covering group form a lattice, corresponding to the lattice of subgroups of the center of the universal covering group: inclusion of subgroups corresponds to covering of quotient groups. The maximal element is the universal covering group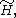 while the minimal element is the universal covering group mod its center, 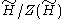.This corresponds algebraically to the universal perfect central extension (called "covering group", by analogy) as the maximal element, and a group mod its center as minimal element.
This is particularly important for Lie groups, as these groups are all the (connected) realizations of a particular Lie algebra. For many Lie groups the center is the group of scalar matrices, and thus the group mod its center is the projectivization of the Lie group. These covers are important in studying projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of Lie groups, and spin representations lead to the discovery of spin groups: a projective representation of a Lie group need not come from a linear representation of the group, but does come from a linear representation of some covering group, in particular the universal covering group. The finite analog led to the covering group or Schur cover, as discussed above.
A key example arises from SL2(R), which has center {±1} and fundamental group Z. It is a double cover of the centerless projective special linear group PSL2(R), which is obtained by taking the quotient by the center. By Iwasawa decomposition
Iwasawa decomposition
In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
, both groups are circle bundles over the complex upper half-plane, and their universal cover
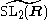is a real line bundle over the half-plane that forms one of Thurston's eight geometriesGeometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
. Since the half-plane is contractible, all bundle structures are trivial. The preimage of SL2(Z) in the universal cover is isomorphic to the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
on three strands.
Lie groups
The above definitions and constructions all apply to the special case of Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. In particular, every covering of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a manifold, and the covering homomorphism becomes a smooth map. Likewise, given any discrete normal subgroup of a Lie group the quotient group is a Lie group and the quotient map is a covering homomorphism.
Two Lie groups are locally isomorphic if and only if the their Lie algebras are isomorphic. This implies that a homomorphism φ : G → H of Lie groups is a covering homomorphism if and only if the induced map on Lie algebras
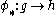
is an isomorphism.
Since for every Lie algebra
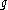there is a unique simply connected Lie group G with Lie algebra 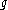, from this follows that the universal convering group of a connected Lie group H is the (unique) simply connected Lie group G having the same Lie algebra as H.Examples
- The universal covering group of the circle group T is the additive group of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R with the covering homomorphism given by the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
exp: R → T. The kernel of the exponential map is isomorphic to Z. - For any integer n we have a covering group of the circle by itself T → T which sends z to zn. The kernel of this homomorphism is the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
consisting of the nth roots of unity. - The rotation group SO(3) has as a universal cover the group SU(2) which is isomorphic to the group of unit quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s Sp(1). This is a double cover since the kernel has order 2. - The unitary groupUnitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) is covered by the compact group T × SU(n) with the covering homomorphism given by p(z, A) = zA. The universal cover is just R × SU(n). - The special orthogonal group SO(n) has a double cover called the spin group Spin(n). For n ≥ 3, the spin group is the universal cover of SO(n).
- For n ≥ 2, the universal cover of the special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(n, R) is not a matrix groupMatrix groupIn mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
(i.e. it has no faithful finite-dimensional representationGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s).