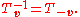.gif)
Translation (geometry)
Encyclopedia

Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
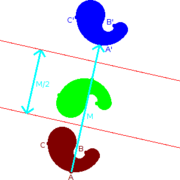
, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
to every point, or as shifting the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of the coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. A translation operator is an operator
 such that
such that 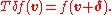
If v is a fixed vector, then the translation Tv will work as Tv(p) = p + v.
If T is a translation, then the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a subset A under the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
T is the translate of A by T. The translate of A by Tv is often written A + v.
In a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, any translation is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
. The set of all translations forms the translation group T, which is isomorphic to the space itself, and a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
E(n ). The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of E(n ) by T is isomorphic to the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n ):
- E(n ) / T ≅ O(n ).
Matrix representation
Since a translation is an affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
but not a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
are normally used to represent the translation operator by a matrix and thus to make it linear. Thus we write the 3-dimensional vector w = (wx, wy, wz) using 4 homogeneous coordinates as w = (wx, wy, wz, 1).
To translate an object by a vector v, each homogeneous vector p (written in homogeneous coordinates) would need to be multiplied by this translation matrix:
-

As shown below, the multiplication will give the expected result:-

The inverse of a translation matrix can be obtained by reversing the direction of the vector:
Similarly, the product of translation matrices is given by adding the vectors:
Because addition of vectors is commutative, multiplication of translation matrices is therefore also commutative (unlike multiplication of arbitrary matrices).
See also
- Translation (physics)Translation (physics)In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
- Translational symmetryTranslational symmetryIn geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
- Transformation matrix
- Rotation matrix
- Scaling (geometry)Scaling (geometry)In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
External links
- Translation Transform at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Geometric Translation (Interactive Animation) at Math Is Fun
- Understanding 2D Translation and Understanding 3D Translation by Roger Germundsson, The Wolfram Demonstrations Project.
-
-