
Unit vector
Encyclopedia
In mathematics
, a unit vector in a normed vector space
is a vector
(often a spatial vector) whose length
is 1 (the unit length). A unit vector is often denoted by a lowercase letter with a "hat
", like this: .
In Euclidean space
, the dot product
of two unit vectors is simply the cosine of the angle between them. This follows from the formula for the dot product, since the lengths are both 1.
The normalized vector or versor of a non-zero vector is the unit vector codirectional with , i.e.,
where is the norm
(or length) of . The term normalized vector is sometimes used as a synonym for unit vector.
The elements of a basis
are usually chosen to be unit vectors. Every vector in the space may be written as a linear combination of unit vectors. The most commonly encountered bases are Cartesian
, polar
, and spherical
coordinates. Each uses different unit vectors according to the symmetry of the coordinate system. Since these systems are encountered in so many different contexts, it is not uncommon to encounter different naming conventions than those used here.
, the unit vectors codirectional with the x, y, and z axes are sometimes referred to as versors of the coordinate system.
These are often written using normal vector notation (e.g. i, or ) rather than the caret notation, and in most contexts it can be assumed that i, j, and k, (or and ) are versors of a Cartesian coordinate system (hence a tern of mutually orthogonal unit vectors). The notations , , , or , with or without hat/caret, are also used, particularly in contexts where i, j, k might lead to confusion with another quantity (for instance with index
symbols such as i, j, k, used to identify an element of a set or array or sequence of variables). These vectors represent an example of a standard basis
.
When a unit vector in space is expressed, with Cartesian notation, as a linear combination of i, j, k, its three scalar components can be referred to as direction cosines. The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector. This is one of the methods used to describe the orientation
(angular position) of a straight line, segment of straight line, oriented axis, or segment of oriented axis (vector).
It is important to note that and are functions of , and are not constant in direction. When differentiating or integrating in cylindrical coordinates, these unit vectors themselves must also be operated on. For a more complete description, see Jacobian matrix. The derivatives with respect to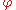 are:
are:
relations are:
The spherical unit vectors depend on both and , and hence there are 5 possible non-zero derivatives. For a more complete description, see Jacobian
. The non-zero derivatives are:
unit vectors equal to the degrees of freedom of the space. For ordinary 3-space, these vectors may be denoted . It is nearly always convenient to define the system to be orthonormal and right-handed
:
where δij is the Kronecker delta (which is one for i = j and zero else) and is the Levi-Civita symbol
(which is one for permutations ordered as ijk and minus one for permutations ordered as kji).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a unit vector in a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
is a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(often a spatial vector) whose length
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
is 1 (the unit length). A unit vector is often denoted by a lowercase letter with a "hat
Circumflex
The circumflex is a diacritic used in the written forms of many languages, and is also commonly used in various romanization and transcription schemes. It received its English name from Latin circumflexus —a translation of the Greek περισπωμένη...
", like this: .
In Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of two unit vectors is simply the cosine of the angle between them. This follows from the formula for the dot product, since the lengths are both 1.
The normalized vector or versor of a non-zero vector is the unit vector codirectional with , i.e.,
where is the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
(or length) of . The term normalized vector is sometimes used as a synonym for unit vector.
The elements of a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
are usually chosen to be unit vectors. Every vector in the space may be written as a linear combination of unit vectors. The most commonly encountered bases are Cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, polar
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
, and spherical
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
coordinates. Each uses different unit vectors according to the symmetry of the coordinate system. Since these systems are encountered in so many different contexts, it is not uncommon to encounter different naming conventions than those used here.
Cartesian coordinates
In the three dimensional Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the unit vectors codirectional with the x, y, and z axes are sometimes referred to as versors of the coordinate system.
These are often written using normal vector notation (e.g. i, or ) rather than the caret notation, and in most contexts it can be assumed that i, j, and k, (or and ) are versors of a Cartesian coordinate system (hence a tern of mutually orthogonal unit vectors). The notations , , , or , with or without hat/caret, are also used, particularly in contexts where i, j, k might lead to confusion with another quantity (for instance with index
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
symbols such as i, j, k, used to identify an element of a set or array or sequence of variables). These vectors represent an example of a standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
.
When a unit vector in space is expressed, with Cartesian notation, as a linear combination of i, j, k, its three scalar components can be referred to as direction cosines. The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector. This is one of the methods used to describe the orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
(angular position) of a straight line, segment of straight line, oriented axis, or segment of oriented axis (vector).
Cylindrical coordinates
The unit vectors appropriate to cylindrical symmetry are: (also designated or ), the distance from the axis of symmetry; , the angle measured counterclockwise from the positive x-axis; and . They are related to the Cartesian basis , , by:- =
- =
It is important to note that and are functions of , and are not constant in direction. When differentiating or integrating in cylindrical coordinates, these unit vectors themselves must also be operated on. For a more complete description, see Jacobian matrix. The derivatives with respect to
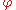 are:
are:Spherical coordinates
The unit vectors appropriate to spherical symmetry are: , the direction in which the radial distance from the origin increases; , the direction in which the angle in the x-y plane counterclockwise from the positive x-axis is increasing; and , the direction in which the angle from the positive z axis is increasing. To minimize degeneracy, the polar angle is usually taken . It is especially important to note the context of any ordered triplet written in spherical coordinates, as the roles of and are often reversed. Here, the American "physics" convention is used. This leaves the azimuthal angle defined the same as in cylindrical coordinates. The CartesianCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
relations are:
The spherical unit vectors depend on both and , and hence there are 5 possible non-zero derivatives. For a more complete description, see Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
. The non-zero derivatives are:
Curvilinear coordinates
In general, a coordinate system may be uniquely specified using a number of linearly independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
unit vectors equal to the degrees of freedom of the space. For ordinary 3-space, these vectors may be denoted . It is nearly always convenient to define the system to be orthonormal and right-handed
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
:
where δij is the Kronecker delta (which is one for i = j and zero else) and is the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
(which is one for permutations ordered as ijk and minus one for permutations ordered as kji).
See also
- Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
- Polar coordinate systemPolar coordinate systemIn mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
- Coordinate systemCoordinate systemIn geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
- Curvilinear coordinatesCurvilinear coordinatesCurvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
- JacobianJacobianIn vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
- Right versor
- Four-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...

