
Glide reflection
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
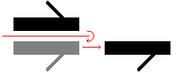
, a glide reflection is a type of isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the Euclidean plane: the combination of a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
in a line and a translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
along that line. Reversing the order of combining gives the same result. Depending on context, we may consider a reflection a special case, where the translation vector is the zero vector.
The combination of a reflection in a line and a translation in a perpendicular direction is a reflection in a parallel line. However, a glide reflection cannot be reduced like that. Thus the effect of a reflection combined with any translation is a glide reflection, with as special case just a reflection. These are the two kinds of indirect isometries in 2D.
For example, there is an isometry consisting of the reflection on the x-axis, followed by translation of one unit parallel to it. In coordinates, it takes
to (x + 1, −y).
It fixes a system of parallel lines.
The isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
generated by just a glide reflection is an infinite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
.
Combining two equal glide reflections gives a pure translation with a translation vector that is twice that of the glide reflection, so the even powers of the glide reflection form a translation group.
In the case of glide reflection symmetry, the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of an object contains a glide reflection, and hence the group generated by it. If that is all it contains, this type is frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
nr. 2.
Example pattern with this symmetry group:
+ +
+++ +++ +++
+
Frieze group nr. 6 (glide-reflections, translations and rotations) is generated by a glide reflection and a rotation about a point on the line of reflection. It is isomorphic to a semi-direct product of Z and C2.
Example pattern with this symmetry group:
+ + + +
+ + + + +
For any symmetry group containing some glide reflection symmetry, the translation vector of any glide reflection is one half of an element of the translation group. If the translation vector of a glide reflection is itself an element of the translation group, then the corresponding glide reflection symmetry reduces to a combination of reflection symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
and translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
.
Glide reflection symmetry with respect to two parallel lines with the same translation implies that there is also translational symmetry in the direction perpendicular to these lines, with a translation distance which is twice the distance between glide reflection lines. This corresponds to wallpaper group
Wallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
pg; with additional symmetry it occurs also in pmg, pgg and p4g.
If there are also true reflection lines in the same direction then they are evenly spaced between the glide reflection lines. A glide reflection line parallel to a true reflection line already implies this situation. This corresponds to wallpaper group cm. The translational symmetry is given by oblique translation vectors from one point on a true reflection line to two points on the next, supporting a rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
with the true reflection line as one of the diagonals. With additional symmetry it occurs also in cmm, p3m1, p31m, p4m and p6m.
In 3D the glide reflection is called a glide plane
Glide plane
In crystallography, a glide plane is symmetry operation describing how a reflection in a plane, followed by a translation parallel with that plane, may leave the crystal unchanged....
. It is a reflection in a plane combined with a translation parallel to the plane.
Glide symmetry can be observed in nature among certain fossils of the Ediacara biota
Ediacara biota
The Ediacara biota consisted of enigmatic tubular and frond-shaped, mostly sessile organisms which lived during the Ediacaran Period . Trace fossils of these organisms have been found worldwide, and represent the earliest known complex multicellular organisms.Simple multicellular organisms such as...
; the machaeridians; and certain palaeoscolecid
Palaeoscolecid
The palaeoscolecids are a group of ecdysozoan worms resembling armoured priapulids. They are known from the Lower Cambrian to the late Silurian; they are mainly found as disarticulated sclerites, but are also preserved in many of the Cambrian lagerstatten...
worms.
Glide reflection in cellular automata
Glide reflection is common in Conway's Game of LifeConway's Game of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
. The four most common spaceships: the glider
Glider (Conway's Life)
The glider is a pattern that travels across the board in Conway's Game of Life. It was first discovered by Richard K. Guy in 1970, while John Conway's group was attempting to track the evolution of the R-pentomino. Gliders are the smallest spaceships, and they travel diagonally at a speed of c/4...
, LWSS, MWSS and HWSS all move using glide reflection. Every two iterations these spaceships appear to have been glide reflected to their new positions. Here is the evolution of the lightweight spaceship:
| o | . | . | o | . | . | . |
| . | . | . | . | o | . | . |
| o | . | . | . | o | . | . |
| . | o | o | o | o | . | . |
| . | . | . | . | . | . | . |
| . | . | . | . | . | . | . |
| . | . | . | o | o | . | . |
| . | o | o | . | o | o | . |
| . | o | o | o | o | . | . |
| . | . | o | o | . | . | . |
| . | . | . | . | . | . | . |
| . | . | o | o | o | o | . |
| . | o | . | . | . | o | . |
| . | . | . | . | . | o | . |
| . | o | . | . | o | . | . |
| . | . | . | o | o | . | . |
| . | . | o | o | o | o | . |
| . | . | o | o | . | o | o |
| . | . | . | . | o | o | . |
| . | . | . | . | . | . | . |
This then carries on glide reflecting in a similar manner.
External links
- Glide Reflection at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

