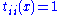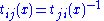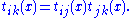Fiber bundle
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and particularly topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a fiber bundle (or, in BrE
British English
British English, or English , is the broad term used to distinguish the forms of the English language used in the United Kingdom from forms used elsewhere...
, fibre bundle) is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure. Specifically, the similarity between the fiber bundle E and a product space B × F is defined using a continuous surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
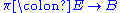
that in small regions of E behaves just like a projection from corresponding regions of B × F to B. The map π, called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space E is known as the total space of the fiber bundle, B as the base space, and F the fiber.
In the trivial case, E is just B × F, and the map π is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles, that is, bundles twisted in the large, include the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
and Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, as well as nontrivial covering spaces. Fiber bundles such as the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and more general vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s play an important role in differential geometry and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, as do principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s.
Mappings which factor over the projection map are known as bundle maps, and the set of fiber bundles forms a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
with respect to such mappings. A bundle map from the base space itself (with the identity mapping as projection) to E is called a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of E. Fiber bundles can be generalized in a number of ways, the most common of which is requiring that the transition between the local trivial patches should lie in a certain topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, known as the structure group, acting on the fiber F.
Formal definition
A fiber bundle consists of the data (E, B, π, F), where E, B, and F are topological spaces and π : E → B is a continuous surjection satisfying a local triviality condition outlined below. The space B is called the base space of the bundle, E the total space, and F the fiber. The map π is called the projection map (or bundle projection). We shall assume in what follows that the base space B is connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
.
We require that for any x in E, there is an open neighborhood U ⊂ B of π(x) (which will be called a trivializing neighborhood) such that π−1(U) is homeomorphic to the product space
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
U × F, in such a way that π carries over to the projection onto the first factor. That is, the following diagram should commute
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
where proj1 : U × F → U is the natural projection and φ : π−1(U) → U × F is a homeomorphism. The set of all {(Ui, φi)} is called a local trivialization of the bundle.
Thus for any p in B, the preimage π−1({p}) is homeomorphic to F and is called the fiber over p. Every fiber bundle π : E → B is an open map, since projections of products are open maps. Therefore B carries the quotient topology determined by the map π.
A fiber bundle (E, B, π, F) is often denoted
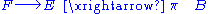
that, in analogy with a short exact sequence, indicates which space is the fiber, total space and base space, as well as the map from total to base space.
A smooth fiber bundle is a fiber bundle in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of smooth manifolds. That is, E, B, and F are required to be smooth manifolds and all the functions above are required to be smooth maps.
Trivial bundle
Let E = B × F and let π : E → B be the projection onto the first factor. Then E is a fiber bundle (of F) over B. Here E is not just locally a product but globally one. Any such fiber bundle is called a trivial bundle. Any fiber bundle over a contractible CW-complex is trivial.Möbius strip

Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
. It has the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
that runs lengthwise along the center of the strip as a base B and a line segment for the fiber F, so the Möbius strip is a bundle of the line segment over the circle. A neighborhood U of a point x ∈ B is an arc; in the picture, this is the length of one of the squares. The preimage
 in the picture is a (somewhat twisted) slice of the strip four squares wide and one long. The homeomorphism φ maps the preimage of U to a slice of a cylinder: curved, but not twisted.
in the picture is a (somewhat twisted) slice of the strip four squares wide and one long. The homeomorphism φ maps the preimage of U to a slice of a cylinder: curved, but not twisted.The corresponding trivial bundle B × F would be a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, but the Möbius strip has an overall "twist". Note that this twist is visible only globally; locally the Möbius strip and the cylinder are identical (making a single vertical cut in either gives the same space).
Klein bottle
A similar nontrivial bundle is the Klein bottleKlein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
which can be viewed as a "twisted" circle bundle over another circle. The corresponding non-twisted (trivial) bundle is the 2-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, S1 × S1.
 |
 |
Covering map
A covering spaceCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
is a fiber bundle such that the bundle projection is a local homeomorphism
Local homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
. It follows in particular, that the fiber is a discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
Vector and principal bundles
A special class of fiber bundles, called vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s, are those whose fibers are vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s (to qualify as a vector bundle the structure group of the bundle — see below — must be a linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
). Important examples of vector bundles include the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
and cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of a smooth manifold. From any vector bundle, one can construct the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of bases which is a principal bundle (see below).
Another special class of fiber bundles, called principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, are bundles on whose fibers a free and transitive action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by a group G is given, so that each fiber is a principal homogeneous space
Principal homogeneous space
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
. The bundle is often specified along with the group by referring to it as a principal G-bundle. The group G is also the structure group of the bundle. Given a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
ρ of G on a vector space V, a vector bundle with ρ(G)⊆Aut(V) as a structure group may be constructed, known as the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
.
Sphere bundles
A sphere bundle is a fiber bundle whose fiber is an n-sphereHypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
. Given a vector bundle E with a metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
(such as the tangent bundle to a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
) one can construct the associated unit sphere bundle, for which the fiber over a point x is the set of all unit vectors in Ex. When the vector bundle in question is the tangent bundle T(M), the unit sphere bundle is known as the unit tangent bundle
Unit tangent bundle
In Riemannian geometry, a branch of mathematics, the unit tangent bundle of a Riemannian manifold , denoted by UT or simply UTM, is the unit sphere bundle for the tangent bundle T...
, and is denoted UT(M).
A sphere bundle is partially characterized by its Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
, which is a degree n+1 cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
class in the total space of the bundle. In the case n=1 the sphere bundle is called a circle bundle and the Euler class is equal to the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
, which characterizes the topology of the bundle completely. For any n, given the Euler class of a bundle, one can calculate its cohomology using a long exact sequence called the Gysin sequence
Gysin sequence
In the field of mathematics known as algebraic topology, the Gysin sequence is a long exact sequence which relates the cohomology classes of the base space, the fiber and the total space of a sphere bundle. The Gysin sequence is a useful tool for calculating the cohomology rings given the Euler...
.
Mapping tori
If X is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and f:X → X is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
then the mapping torus
Mapping torus
In mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f...
Mf has a natural structure of a fiber bundle over the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with fiber X. Mapping tori of homeomorphisms of surfaces are of particular importance in 3-manifold topology
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
.
Quotient spaces
If G is a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and H is a closed subgroup, then under some circumstances, the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
G/H together with the quotient map π : G → G/H is a fiber bundle, whose fiber is the topological space H. A necessary and sufficient condition for (G,G/H,π,H) to form a fiber bundle is that the mapping π admit local cross-sections .
The most general conditions under which the quotient map will admit local cross-sections are not known, although if G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and H a closed subgroup (and thus a Lie subgroup by Cartan's theorem
Cartan's theorem
In mathematics, three results in Lie group theory are called Cartan's theorem, named after Élie Cartan:See also Cartan's theorems A and B, results of Henri Cartan, and Cartan's lemma for various other results attributed to Élie and Henri Cartan....
), then the quotient map is a fiber bundle. One example of this is the Hopf fibration, S3 → S2 which is a fiber bundle over the sphere S2 whose total space is S3. From the perspective of Lie groups, S3 can be identified with the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(2). The abelian subgroup of diagonal matrices is isomorphic to the circle group U(1), and the quotient SU(2)/U(1) is diffeomorphic to the sphere.
More generally, if G is any topological group and H a closed subgroup which also happens to be a Lie group, then G → G/H is a fiber bundle.
Sections
A section (or cross section) of a fiber bundle is a continuous map f : B → E such that π(f(x))=x for all x in B. Since bundles do not in general have globally defined sections, one of the purposes of the theory is to account for their existence. The obstructionObstruction theory
In mathematics, obstruction theory is a name given to two different mathematical theories, both of which yield cohomological invariants.-In homotopy theory:...
to the existence of a section can often be measured by a cohomology class, which leads to the theory of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
The most well-known example is the hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
, where the Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is the obstruction to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of the 2-sphere having a nowhere vanishing section.
Often one would like to define sections only locally (especially when global sections do not exist). A local section of a fiber bundle is a continuous map f : U → E where U is an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in B and π(f(x))=x for all x in U. If (U, φ) is a local trivialization chart then local sections always exist over U. Such sections are in 1-1 correspondence with continuous maps U → F. Sections form a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.
Structure groups and transition functions
Fiber bundles often come with a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of symmetries which describe the matching conditions between overlapping local trivialization charts. Specifically, let G be a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
which acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
continuously on the fiber space F on the left. We lose nothing if we require G to act effectively on F so that it may be thought of as a group of homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s of F. A G-atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
for the bundle (E, B, π, F) is a local trivialization such that for any two overlapping charts (Ui, φi) and (Uj, φj) the function
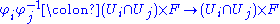
is given by
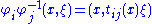
where tij : Ui ∩ Uj → G is a continuous map called a transition function. Two G-atlases are equivalent if their union is also a G-atlas. A G-bundle is a fiber bundle with an equivalence class of G-atlases. The group G is called the structure group of the bundle; the analogous term in physics is gauge group.
In the smooth category, a G-bundle is a smooth fiber bundle where G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and the corresponding action on F is smooth and the transition functions are all smooth maps.
The transition functions tij satisfy the following conditions
The third condition applies on triple overlaps Ui ∩ Uj ∩ Uk and is called the cocycle condition (see Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
). The importance of this is that the transition functions determine the fiber bundle (if one assumes the Čech cocycle condition).
A principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
is a G-bundle where the fiber F is a principal homogeneous space
Principal homogeneous space
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
for the left action of G itself (equivalently, one can specify that the action of G on the fiber F is free and transitive). In this case, it is often a matter of convenience to identify F with G and so obtain a (right) action of G on the principal bundle.
Bundle maps
It is useful to have notions of a mapping between two fiber bundles. Suppose that M and N are base spaces, and πE : E → M and πF : F → N are fiber bundles over M and N, respectively. A bundle mapBundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
(or bundle morphism) consists of a pair of continuous functions

such that
 . That is, the following diagram commutes
. That is, the following diagram commutesCommutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
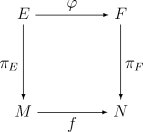
For fiber bundles with structure group G (such as a principal bundle), bundle morphisms are also required to be G-equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
on the fibers.
In case the base spaces M and N coincide, then a bundle morphism over M from the fiber bundle πE : E → M to πF : F → M is a map φ : E → F such that
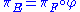 . That is, the diagram commutes
. That is, the diagram commutes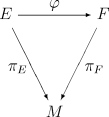
A bundle isomorphism is a bundle map which is also a homeomorphism.
Differentiable fiber bundles
In the category of differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s, fiber bundles arise naturally as submersions
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
of one manifold to another. Not every (differentiable) submersion ƒ : M → N from a differentiable manifold M to another differentiable manifold N gives rise to a differentiable fiber bundle. For one thing, the map must be surjective. However, this necessary condition is not quite sufficient, and there are a variety of sufficient conditions in common use.
If M and N are compact and connected, then any submersion f : M → N gives rise to a fiber bundle in the sense that there is a fiber space F diffeomorphic to each of the fibers such that (E,B,π,F) = (M,N,ƒ,F) is a fiber bundle. (Surjectivity of ƒ follows by the assumptions already given in this case.) More generally, the assumption of compactness can be relaxed if the submersion ƒ : M → N is assumed to be a surjective proper map
Proper map
In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
, meaning that ƒ−1(K) is compact for every compact subset K of N. Another sufficient condition, due to , is that if ƒ : M → N is a surjective submersion
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
with M and N differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s such that the preimage ƒ−1{x} is compact and connected
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
for all x ∈ N, then ƒ admits a compatible fiber bundle structure .
Generalizations
- The notion of a bundleBundle (mathematics)In mathematics, a bundle is a generalization of a fiber bundle dropping the condition of a local product structure. The requirement of a local product structure rests on the bundle having a topology. Without this requirement, more general objects can be considered bundles. For example, one can...
applies to many more categories in mathematics, at the expense of appropriately modifying the local triviality condition. - In topology, a fibrationFibrationIn topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
is a mapping π : E → B which has certain homotopy-theoretic properties in common with fiber bundles. Specifically, under mild technical assumptions a fiber bundle always has the homotopy lifting propertyHomotopy lifting propertyIn mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
or homotopy covering property (see Steenrod 1951, 11.7, for details). This is the defining property of a fibration.
See also
- Covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
- FibrationFibrationIn topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
- Gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
- Hopf bundleHopf bundleIn the mathematical field of topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle...
- Principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
- Pullback bundlePullback bundleIn mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
- Universal bundleUniversal bundleIn mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group G, is a specific bundle over a classifying space BG, such that every bundle with the given structure group G over M is a pullback by means of a continuous map-In the CW complex...
External links
- Fiber Bundle, PlanetMath
- Making John Robinson's Symbolic Sculpture `Eternity'
- Sardanashvily, G.Gennadi SardanashvilyGennadi Sardanashvily is a theoretical physicist, a principal research scientist of Moscow State University.- Biography :...
, Fibre bundles, jet manifolds and Lagrangian theory. Lectures for theoreticians,arXiv: 0908.1886