Akhmim wooden tablet
Encyclopedia
The Akhmim wooden tablets or Cairo wooden tablets (Cairo Cat. 25367 and 25368) are two ancient Egypt
ian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed by a mathematical text. The text is dated to year 38 (it was at first thought to be from year 28) of an otherwise unnamed king. The general dating to the early Egyptian Middle Kingdom combined with the high regnal year suggests that the tables may date to the reign of Senusret I
, ca. 1950 BC. The second tablet also lists several servants and further contains mathematical texts.
The tablets are currently housed in Cairo's Museum of Egyptian Antiquities. The text was reported by Daressy
in 1901 and later analyzed and published in 1906.
The first half of the tablet details five divisions of a hekat by 3, 7, 10, 11 and 13. The answers were written in Eye of Horus
quotients, and Egyptian fraction remainders, scaled to a 1/320th factor named ro. The second half of the document proved the correctness of the five division answers by multiplying the two-part quotient and remainder answer by its respective divisor (3, 7, 10, 11 and 13).
In 2002 Hana Vymazalová
obtained a fresh copy of the text from the Cairo Museum, and confirmed that all five two-part answers were correctly checked for accuracy by the scribe. Typographical errors in Daressy's copy of two problems, the division by 11 and 13 data, were corrected at this time as well. The proof that all five divisions had been exact was suspected by Daressy, but was not proven in 1906.
In modern mathematical notation we might say that the scribe showed that 3 times the hekat fraction (1/4 + 1/16 + 1/64) is equal to 63/64 and that 3 times the remainder part ((1 + 2/3) ro) is equal to 5 ro, which is equal to 1/64 th of a hekat.
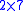is said to be 12 and the double of that 24 in all of the copies of the problem. The mistake takes place in exactly the same place in each of the versions of this problem, but the scribe manages to find the correct answer in spite of this error. The fourth copy of the 1/7 division contains an extra error in one of the lines. The mistakes made suggest that the scribe may have been carelessly copying the problems from some other source.
The fraction 1/11 computation occurs four times and the problems appear right next to one another leaving the impression that the scribe was practicing the computation procedure. The 1/13 computation appears once in its complete form and twice more with only partial computations. There are errors in the computations, but the scribe does find the correct answer. The 1/10 computation is the only fraction computed only once. There are no mistakes in the computations for this problem.
contains several examples of hekat division. The problems are somewhat different in nature but the expression of measures of grain in terms of Horus eye fractions of the hekat and remainders in terms of ro appear in several problems. Some examples include:
The Ebers Papyrus
is a famous late Middle Kingdom medical text. Its raw data was written in hekat one-parts suggested by the AWT, handling divisors greater than 64.
Ancient Egypt
Ancient Egypt was an ancient civilization of Northeastern Africa, concentrated along the lower reaches of the Nile River in what is now the modern country of Egypt. Egyptian civilization coalesced around 3150 BC with the political unification of Upper and Lower Egypt under the first pharaoh...
ian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed by a mathematical text. The text is dated to year 38 (it was at first thought to be from year 28) of an otherwise unnamed king. The general dating to the early Egyptian Middle Kingdom combined with the high regnal year suggests that the tables may date to the reign of Senusret I
Senusret I
Senusret I was the second pharaoh of the Twelfth Dynasty of Egypt. He ruled from 1971 BC to 1926 BC, and was one of the most powerful kings of this Dynasty. He was the son of Amenemhat I and his wife Nefertitanen. His wife and sister was Neferu. She was also the mother of the successor Amenemhat II...
, ca. 1950 BC. The second tablet also lists several servants and further contains mathematical texts.
The tablets are currently housed in Cairo's Museum of Egyptian Antiquities. The text was reported by Daressy
Georges Émile Jules Daressy
Georges Émile Jules Daressy was a French Egyptologist.He worked from 1887 in the Egyptian Museum in Cairo. Amongst his responsibilies was the museums its move from Bulaq to Giza in 1891, and then to the present day location in 1901. He is an important author of the general catalog of the museum...
in 1901 and later analyzed and published in 1906.
The first half of the tablet details five divisions of a hekat by 3, 7, 10, 11 and 13. The answers were written in Eye of Horus
Eye of Horus
The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet...
quotients, and Egyptian fraction remainders, scaled to a 1/320th factor named ro. The second half of the document proved the correctness of the five division answers by multiplying the two-part quotient and remainder answer by its respective divisor (3, 7, 10, 11 and 13).
In 2002 Hana Vymazalová
Hana Vymazalová
Hana Vymazalová, born 1978, is a Czech Egyptologist. She graduated in Egyptology and Logic at the Faculty of Arts, Charles University in Prague....
obtained a fresh copy of the text from the Cairo Museum, and confirmed that all five two-part answers were correctly checked for accuracy by the scribe. Typographical errors in Daressy's copy of two problems, the division by 11 and 13 data, were corrected at this time as well. The proof that all five divisions had been exact was suspected by Daressy, but was not proven in 1906.
1/3 case
The first problem divides 1 hekat by writing it as 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + (5 ro)(which equals 1) and dividing that expression by 3.- The scribe first divided the remainder of 5 ro by 3, and determined that this was equal to (1 + 2/3) ro.
- Next the scribe finds 1/3 of the rest of the equation and determines it is equal to
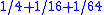. - The final step in the problem consists of checking that the answer is correct and the scribe multiplies
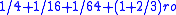by 3 and shows that the answer is 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + (5 ro), which he knows is equal to 1.
In modern mathematical notation we might say that the scribe showed that 3 times the hekat fraction (1/4 + 1/16 + 1/64) is equal to 63/64 and that 3 times the remainder part ((1 + 2/3) ro) is equal to 5 ro, which is equal to 1/64 th of a hekat.
The other fractions
The other problems on the tablets are computed using a different technique. The scribe uses the fact that 1 hekat = 320 ro and now divides 320 by 7, 10, 11 and 13 to find the required expressions. For instance in the 1/7 computation the division of 320 by 7 gives 45 + 1/2 + 1/7 + 1/14 ro. This is equivalent to 1/8 + 1/64 hekat + (1/2 + 1/7 + 1/14) ro. Checking the work required the scribe to multiply this equation by 7 and showing that the result was 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + (5 ro) again.Accuracy
The computations show several mistakes. For instance in the 1/7 computations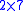 is said to be 12 and the double of that 24 in all of the copies of the problem. The mistake takes place in exactly the same place in each of the versions of this problem, but the scribe manages to find the correct answer in spite of this error. The fourth copy of the 1/7 division contains an extra error in one of the lines. The mistakes made suggest that the scribe may have been carelessly copying the problems from some other source.The fraction 1/11 computation occurs four times and the problems appear right next to one another leaving the impression that the scribe was practicing the computation procedure. The 1/13 computation appears once in its complete form and twice more with only partial computations. There are errors in the computations, but the scribe does find the correct answer. The 1/10 computation is the only fraction computed only once. There are no mistakes in the computations for this problem.
Hekat problems in other texts
The Rhind Mathematical PapyrusRhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
contains several examples of hekat division. The problems are somewhat different in nature but the expression of measures of grain in terms of Horus eye fractions of the hekat and remainders in terms of ro appear in several problems. Some examples include:
- Problems 35-38 in the Rhind Mathematical Papyrus find fractions of the hekat. The problems in this section are equivalent to what we now call linear equations. Problem 35 for instance can be restated as
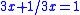, what is x? The answer is first computed to be 1/5 + 1/10 hekat. This is rewritten as a Horus eye fraction by multiplying 1 hekat = 320 ro by (1/5 + 1/10) giving 96 ro. This is determined to be (1/4 + 1/32 + 1/64) hekat + 1 ro. This fraction is multiplied by (3 + 1/3) to check that this really gives 1 hekat. - Problem 47 provides a list of fractions of 100 hekat.
- Problem 80 gives 5 short tables listing Horus eye fractions of the hekat and the equivalent regular fractions as well as expressions in terms of another unit called the hinu.
The Ebers Papyrus
Ebers papyrus
The Ebers Papyrus, also known as Papyrus Ebers, is an Egyptian medical papyrus dating to circa 1550 BC. Among the oldest and most important medical papyri of ancient Egypt, it was purchased at Luxor, in the winter of 1873–74 by Georg Ebers...
is a famous late Middle Kingdom medical text. Its raw data was written in hekat one-parts suggested by the AWT, handling divisors greater than 64.
External links
Scaled AWT Remainders- http://www.whonamedit.com/synd.cfm/443.html