Uncountable set
Encyclopedia
In mathematics
, an uncountable set is an infinite set that contains too many elements to be countable
. The uncountability of a set is closely related to its cardinal number
: a set is uncountable if its cardinal number is larger than that of the set of all natural number
s.
The first three of these characterizations can be proven equivalent in Zermelo–Fraenkel set theory
without the axiom of choice, but the equivalence of the third and fourth cannot be proved without additional choice principles.
s; Cantor's diagonal argument
shows that this set is uncountable. The diagonalization proof technique can also be used to show that several other sets are uncountable, such as the set of all infinite sequence
s of natural number
s and the set of all subset
s of the set of natural numbers. The cardinality of R is often called the cardinality of the continuum
and denoted by c, or
, or 
(beth-one
).
The Cantor set
is an uncountable subset of R. The Cantor set is a fractal
and has Hausdorff dimension
greater than zero but less than one (R has dimension one). This is an example of the following fact: any subset of R of Hausdorff dimension strictly greater than zero must be uncountable.
Another example of an uncountable set is the set of all functions from R to R. This set is even "more uncountable" than R in the sense that the cardinality of this set is
(beth-two), which is larger than 
.
A more abstract example of an uncountable set is the set of all countable ordinal number
s, denoted by Ω (omega
) or ω1. The cardinality of Ω is denoted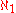
(aleph-one
). It can be shown, using the axiom of choice, that
is the smallest uncountable cardinal number. Thus either 
, the cardinality of the reals, is equal to 
or it is strictly larger. Georg Cantor
was the first to propose the question of whether
is equal to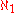 
. In 1900, David Hilbert
posed this question as the first of his 23 problems
. The statement that
is now called the continuum hypothesis
and is known to be independent of the Zermelo–Fraenkel axioms for set theory
(including the axiom of choice).
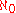(namely, the cardinalities of Dedekind-finite infinite sets). Sets of these cardinalities satisfy the first three characterizations above but not the fourth characterization. Because these sets are not larger than the natural numbers in the sense of cardinality, some may not want to call them uncountable.
If the axiom of choice holds, the following conditions on a cardinal
are equivalent:
However, these may all be different if the axiom of choice fails. So it is not obvious which one is the appropriate generalization of "uncountability" when the axiom fails. It may be best to avoid using the word in this case and specify which of these one means.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an uncountable set is an infinite set that contains too many elements to be countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
. The uncountability of a set is closely related to its cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
: a set is uncountable if its cardinal number is larger than that of the set of all natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
Characterizations
There are many equivalent characterizations of uncountability. A set X is uncountable if and only if any of the following conditions holds:- There is no injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from X to the set of natural numbers. - X is nonempty and every ω-sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of elements of X fails to include at least one element of X. That is, X is nonempty and there is no surjective functionSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
from the natural numbers to X. - The cardinality of X is neither finite nor equal to
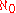(aleph-nullAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
, the cardinality of the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s). - The set X has cardinality strictly greater than
.
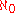The first three of these characterizations can be proven equivalent in Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
without the axiom of choice, but the equivalence of the third and fourth cannot be proved without additional choice principles.
Examples
The best known example of an uncountable set is the set R of all real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s; Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
shows that this set is uncountable. The diagonalization proof technique can also be used to show that several other sets are uncountable, such as the set of all infinite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s and the set of all subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the set of natural numbers. The cardinality of R is often called the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
and denoted by c, or
, or (beth-oneCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
).
The Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is an uncountable subset of R. The Cantor set is a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
and has Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
greater than zero but less than one (R has dimension one). This is an example of the following fact: any subset of R of Hausdorff dimension strictly greater than zero must be uncountable.
Another example of an uncountable set is the set of all functions from R to R. This set is even "more uncountable" than R in the sense that the cardinality of this set is
(beth-two), which is larger than .A more abstract example of an uncountable set is the set of all countable ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s, denoted by Ω (omega
Omega
Omega is the 24th and last letter of the Greek alphabet. In the Greek numeric system, it has a value of 800. The word literally means "great O" , as opposed to omicron, which means "little O"...
) or ω1. The cardinality of Ω is denoted
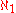(aleph-oneAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
). It can be shown, using the axiom of choice, that
is the smallest uncountable cardinal number. Thus either , the cardinality of the reals, is equal to or it is strictly larger. Georg CantorGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
was the first to propose the question of whether
is equal to 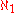. In 1900, David HilbertDavid Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
posed this question as the first of his 23 problems
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
. The statement that
is now called the continuum hypothesisContinuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
and is known to be independent of the Zermelo–Fraenkel axioms for set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
(including the axiom of choice).
Without the axiom of choice
Without the axiom of choice, there might exist cardinalities incomparable to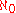 (namely, the cardinalities of Dedekind-finite infinite sets). Sets of these cardinalities satisfy the first three characterizations above but not the fourth characterization. Because these sets are not larger than the natural numbers in the sense of cardinality, some may not want to call them uncountable.If the axiom of choice holds, the following conditions on a cardinal
are equivalent:
and
, where 
and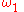 
is least initial ordinal greater than 
However, these may all be different if the axiom of choice fails. So it is not obvious which one is the appropriate generalization of "uncountability" when the axiom fails. It may be best to avoid using the word in this case and specify which of these one means.