Countable set
Encyclopedia
In mathematics
, a countable set is a set with the same cardinality (number
of elements) as some subset
of the set of natural number
s. A set that is not countable is called uncountable
. The term was originated by Georg Cantor
. The elements of a countable set can be counted one at a time—although the counting may never finish, every element of the set will eventually be associated with a natural number.
Some authors use countable set to mean a set with the same cardinality as the set of natural numbers. The difference between the two definitions is that under the former, finite sets are also considered to be countable, while under the latter definition, they are not considered to be countable. To resolve this ambiguity, the term at most countable is sometimes used for the former notion, and countably infinite for the latter. The term denumerable can also be used to mean countably infinite, or countable, in contrast with the term nondenumerable.
f from S to the natural numbers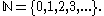
If f is also surjective
and therefore bijective
, then S is called countably infinite.
As noted above, this terminology is not universal: Some authors use countable to mean what is here called "countably infinite," and to not include finite sets.
For alternative (equivalent) formulations of the definition in terms of a bijective function or a surjective function, see the section Formal definition and properties below.
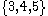 . This is only effective for small sets, however; for larger sets, this would be time-consuming and error-prone. Instead of listing every single element, sometimes an ellipsis ("...") is used, if the writer believes that the reader can easily guess what is missing; for example,
. This is only effective for small sets, however; for larger sets, this would be time-consuming and error-prone. Instead of listing every single element, sometimes an ellipsis ("...") is used, if the writer believes that the reader can easily guess what is missing; for example, 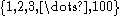 presumably denotes the set of integer
presumably denotes the set of integer
s from 1 to 100. Even in this case, however, it is still possible to list all the elements, because the set is finite; it has a specific number of elements.
Some sets are infinite; these sets have more than n elements for any integer n. For example, the set of natural numbers, denotable by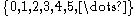 , has infinitely many elements, and we cannot use any normal number to give its size. Nonetheless, it turns out that infinite sets do have a well-defined notion of size (or more properly, of cardinality, which is the technical term for the number of elements in a set), and not all infinite sets have the same cardinality.
, has infinitely many elements, and we cannot use any normal number to give its size. Nonetheless, it turns out that infinite sets do have a well-defined notion of size (or more properly, of cardinality, which is the technical term for the number of elements in a set), and not all infinite sets have the same cardinality.
To understand what this means, we must first examine what it does not mean. For example, there are infinitely many odd integers, infinitely many even integers, and (hence) infinitely many integers overall. However, it turns out that the number of odd integers, which is the same as the number of even integers, is also the same as the number of integers overall. This is because we arrange things such that for every integer, there is a distinct odd integer: ... −2 → −3, −1 → −1, 0 → 1, 1 → 3, 2 → 5, ...; or, more generally, n → 2n + 1. What we have done here is arranged the integers and the odd integers into a one-to-one correspondence (or bijection
), which is a function
that maps between two sets such that each element of each set corresponds to a single element in the other set.
However, not all infinite sets have the same cardinality. For example, Georg Cantor
(who introduced this branch of mathematics) demonstrated that the real number
s cannot be put into one-to-one correspondence with the natural numbers (non-negative integers), and therefore that the set of real numbers has a greater cardinality than the set of natural numbers.
A set is countable if: (1) it is finite, or (2) it has the same cardinality (size) as the set of natural numbers. Equivalently, a set is countable if it has the same cardinality as some subset
of the set of natural numbers. Otherwise, it is uncountable.
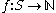
from S to the natural numbers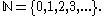
It might seem natural to divide the sets into different classes: put all the sets containing one element together; all the sets containing two elements together; ...; finally, put together all infinite sets and consider them as having the same size.
This view is not tenable, however, under the natural definition of size.
To elaborate this we need the concept of a bijection
. Although a "bijection" seems a more advanced concept than a number, the usual development of mathematics in terms of set theory defines functions before numbers, as they are based on much simpler sets. This is where the concept of a bijection comes in: define the correspondence
Since every element of { a, b, c } is paired with precisely one element of { 1, 2, 3 }, and vice versa, this defines a bijection.
We now generalize this situation and define two sets to be of the same size if (and only if) there is a bijection between them. For all finite sets this gives us the usual definition of "the same size". What does it tell us about the size of infinite sets?
Consider the sets A = { 1, 2, 3, ... }, the set of positive integer
s and B = { 2, 4, 6, ... }, the set of even positive integers. We claim that, under our definition, these sets have the same size, and that therefore B is countably infinite. Recall that to prove this we need to exhibit a bijection between them. But this is easy, using n ↔ 2n, so that
As in the earlier example, every element of A has been paired off with precisely one element of B, and vice versa. Hence they have the same size. This gives an example of a set which is of the same size as one of its proper subsets, a situation which is impossible for finite sets.
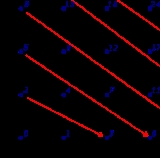
Likewise, the set of all ordered pair
s of natural numbers is countably infinite, as can be seen by following a path like the one in the picture: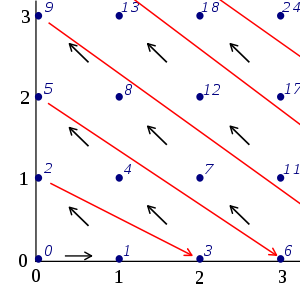 The resulting mapping is like this:
The resulting mapping is like this:
It is evident that this mapping will cover all such ordered pairs.
Interestingly: if you treat each pair as being the numerator and denominator of a vulgar fraction, then for every positive fraction, we can come up with a distinct number corresponding to it. This representation includes also the natural numbers, since every natural number is also a fraction N/1. So we can conclude that there are exactly as many positive rational numbers as there are positive integers. This is true also for all rational numbers, as can be seen below (a more complex presentation is needed to deal with negative numbers).
Theorem: The Cartesian product
of finitely many countable sets is countable.
This form of triangular mapping
recursively
generalizes to vectors
of finitely many natural numbers by repeatedly mapping the first two elements to a natural number. For example, (0,2,3) maps to (5,3) which maps to 39.
Sometimes more than one mapping is useful. This is where you map the set which you want to show countably infinite, onto another set; and then map this other set to the natural numbers. For example, the positive rational number
s can easily be mapped to (a subset of) the pairs of natural numbers because p/q maps to (p, q).
What about infinite subsets of countably infinite sets? Do these have fewer elements than N?
Theorem: Every subset of a countable set is countable. In particular, every infinite subset of a countably infinite set is countably infinite.
For example, the set of prime number
s is countable, by mapping the n-th prime number to n:
What about sets being "larger than" N? An obvious place to look would be Q, the set of all rational number
s, which intuitively may seem much bigger than N. But looks can be deceiving, for we assert:
Theorem: Q (the set of all rational numbers) is countable.
Q can be defined as the set of all fractions a/b where a and b are integers and b > 0. This can be mapped onto the subset of ordered triples of natural numbers (a, b, c) such that a ≥ 0, b > 0, a and b are coprime
, and c ∈ {0, 1} such that c = 0 if a/b ≥ 0 and c = 1 otherwise.
By a similar development, the set of algebraic number
s is countable, and so is the set of definable number
s.
Theorem: (Assuming the axiom of countable choice
) The union
of countably many countable sets is countable.
For example, given countable sets a, b, c ...
Using a variant of the triangular enumeration we saw above:
Note that this only works if the sets a, b, c,... are disjoint. If not, then the union is even smaller and is therefore also countable by a previous theorem.
Also note that the axiom of countable choice
is needed in order to index all of the sets a, b, c,...
Theorem: The set of all finite-length sequence
s of natural numbers is countable.
This set is the union of the length-1 sequences, the length-2 sequences, the length-3 sequences, each of which is a countable set (finite Cartesian product). So we are talking about a countable union of countable sets, which is countable by the previous theorem.
Theorem: The set of all finite subset
s of the natural numbers is countable.
If you have a finite subset, you can order the elements into a finite sequence. There are only countably many finite sequences, so also there are only countably many finite subsets.
The following theorem gives equivalent formulations in terms of a bijective function or a surjective function
. A proof of this result can be found in Lang's text.
Theorem: Let S be a set. The following statements are equivalent:
Several standard properties follow easily from this theorem. We present them here tersely. For a gentler presentation see the sections above. Observe that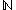 in the theorem can be replaced with any countably infinite set. In particular we have the following Corollary.
in the theorem can be replaced with any countably infinite set. In particular we have the following Corollary.
Corollary: Let S and T be sets.
Proof: For (1) observe that if T is countable there is an injective function
 Then if
Then if
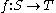 is injective
is injective
the composition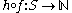 is injective, so S is countable.
is injective, so S is countable.
For (2) observe that if S is countable there is a surjective function
 Then if
Then if 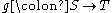 is surjective the composition
is surjective the composition  is surjective, so T is countable.
is surjective, so T is countable.
Proposition: Any subset of a countable set is countable.
Proof: The restriction of an injective function to a subset of its domain
is still injective.
Proposition: The Cartesian product
of two countable sets A and B is countable.
Proof: Note that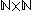 is countable as a consequence of the definition because the function
is countable as a consequence of the definition because the function 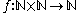 given by
given by 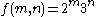 is injective. It then follows from the Basic Theorem and the Corollary that the Cartesian product of any two countable sets is countable. This follows because if A and B are countable there are surjections
is injective. It then follows from the Basic Theorem and the Corollary that the Cartesian product of any two countable sets is countable. This follows because if A and B are countable there are surjections 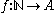 and
and 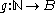 . So
. So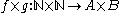
is a surjection from the countable set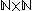 to the set
to the set
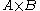 and the Corollary implies
and the Corollary implies 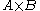 is countable. This result generalizes to the Cartesian product of any finite collection of countable sets and the proof follows by induction
is countable. This result generalizes to the Cartesian product of any finite collection of countable sets and the proof follows by induction
on the number of sets in the collection.
Proposition: The integers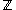 are countable and the rational numbers
are countable and the rational numbers 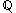 are countable.
are countable.
Proof: The integers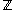 are countable because the function
are countable because the function 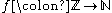 given by
given by 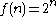 if n is non-negative and
if n is non-negative and 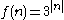 if n is negative is an injective function. The rational numbers
if n is negative is an injective function. The rational numbers 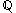 are countable because the function
are countable because the function 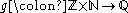 given by
given by 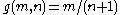 is a surjection from the countable set
is a surjection from the countable set 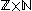 to the rationals
to the rationals 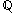 .
.
Proposition: If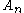 is a countable set for each
is a countable set for each 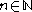 then
then  is countable.
is countable.
Proof: This is a consequence of the fact that for each n there is a surjective function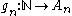 and hence the function
and hence the function
given by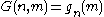 is a surjection. Since
is a surjection. Since 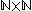 is countable the Corollary implies
is countable the Corollary implies  is countable. We are using the axiom of countable choice
is countable. We are using the axiom of countable choice
in this proof in order to pick for each a surjection
a surjection 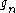 from the non-empty collection of surjections from
from the non-empty collection of surjections from 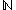 to
to  .
.
Cantor's Theorem
asserts that if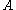 is a set and
is a set and  is its power set, i.e. the set of all subsets of
is its power set, i.e. the set of all subsets of 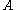 , then there is no surjective function from
, then there is no surjective function from 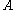 to
to  . A proof is given in the article Cantor's Theorem
. A proof is given in the article Cantor's Theorem
. As an immediate consequence of this and the Basic Theorem above we have:
Proposition: The set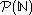 is not countable; i.e. it is uncountable.
is not countable; i.e. it is uncountable.
For an elaboration of this result see Cantor's diagonal argument
.
The set of real number
s is uncountable (see Cantor's first uncountability proof
), and so is the set of all infinite sequence
s of natural numbers. A topological proof for the uncountability of the real numbers is described at finite intersection property
.
) of ZFC set theory, then there is a minimal standard model (see Constructible universe
). The Löwenheim-Skolem theorem can be used to show that this minimal model is countable. The fact that the notion of "uncountability" makes sense even in this model, and in particular that this model M contains elements which are
was seen as paradoxical in the early days of set theory, see Skolem's paradox
.
The minimal standard model includes all the algebraic number
s and all effectively computable transcendental number
s, as well as many other kinds of numbers.
in various ways, e.g.:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a countable set is a set with the same cardinality (number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
of elements) as some subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. A set that is not countable is called uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
. The term was originated by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
. The elements of a countable set can be counted one at a time—although the counting may never finish, every element of the set will eventually be associated with a natural number.
Some authors use countable set to mean a set with the same cardinality as the set of natural numbers. The difference between the two definitions is that under the former, finite sets are also considered to be countable, while under the latter definition, they are not considered to be countable. To resolve this ambiguity, the term at most countable is sometimes used for the former notion, and countably infinite for the latter. The term denumerable can also be used to mean countably infinite, or countable, in contrast with the term nondenumerable.
Definition
A set S is called countable if there exists an injective functionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
f from S to the natural numbers
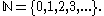
If f is also surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
and therefore bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, then S is called countably infinite.
As noted above, this terminology is not universal: Some authors use countable to mean what is here called "countably infinite," and to not include finite sets.
For alternative (equivalent) formulations of the definition in terms of a bijective function or a surjective function, see the section Formal definition and properties below.
Introduction
A set is a collection of elements, and may be described in many ways. One way is simply to list all of its elements; for example, the set consisting of the integers 3, 4, and 5 may be denoted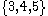 . This is only effective for small sets, however; for larger sets, this would be time-consuming and error-prone. Instead of listing every single element, sometimes an ellipsis ("...") is used, if the writer believes that the reader can easily guess what is missing; for example,
. This is only effective for small sets, however; for larger sets, this would be time-consuming and error-prone. Instead of listing every single element, sometimes an ellipsis ("...") is used, if the writer believes that the reader can easily guess what is missing; for example, 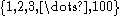 presumably denotes the set of integer
presumably denotes the set of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s from 1 to 100. Even in this case, however, it is still possible to list all the elements, because the set is finite; it has a specific number of elements.
Some sets are infinite; these sets have more than n elements for any integer n. For example, the set of natural numbers, denotable by
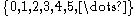 , has infinitely many elements, and we cannot use any normal number to give its size. Nonetheless, it turns out that infinite sets do have a well-defined notion of size (or more properly, of cardinality, which is the technical term for the number of elements in a set), and not all infinite sets have the same cardinality.
, has infinitely many elements, and we cannot use any normal number to give its size. Nonetheless, it turns out that infinite sets do have a well-defined notion of size (or more properly, of cardinality, which is the technical term for the number of elements in a set), and not all infinite sets have the same cardinality.To understand what this means, we must first examine what it does not mean. For example, there are infinitely many odd integers, infinitely many even integers, and (hence) infinitely many integers overall. However, it turns out that the number of odd integers, which is the same as the number of even integers, is also the same as the number of integers overall. This is because we arrange things such that for every integer, there is a distinct odd integer: ... −2 → −3, −1 → −1, 0 → 1, 1 → 3, 2 → 5, ...; or, more generally, n → 2n + 1. What we have done here is arranged the integers and the odd integers into a one-to-one correspondence (or bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
), which is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that maps between two sets such that each element of each set corresponds to a single element in the other set.
However, not all infinite sets have the same cardinality. For example, Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
(who introduced this branch of mathematics) demonstrated that the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s cannot be put into one-to-one correspondence with the natural numbers (non-negative integers), and therefore that the set of real numbers has a greater cardinality than the set of natural numbers.
A set is countable if: (1) it is finite, or (2) it has the same cardinality (size) as the set of natural numbers. Equivalently, a set is countable if it has the same cardinality as some subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the set of natural numbers. Otherwise, it is uncountable.
Formal definition and properties
By definition a set S is countable if there exists an injective functionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
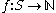
from S to the natural numbers
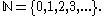
It might seem natural to divide the sets into different classes: put all the sets containing one element together; all the sets containing two elements together; ...; finally, put together all infinite sets and consider them as having the same size.
This view is not tenable, however, under the natural definition of size.
To elaborate this we need the concept of a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
. Although a "bijection" seems a more advanced concept than a number, the usual development of mathematics in terms of set theory defines functions before numbers, as they are based on much simpler sets. This is where the concept of a bijection comes in: define the correspondence
- a ↔ 1, b ↔ 2, c ↔ 3
Since every element of { a, b, c } is paired with precisely one element of { 1, 2, 3 }, and vice versa, this defines a bijection.
We now generalize this situation and define two sets to be of the same size if (and only if) there is a bijection between them. For all finite sets this gives us the usual definition of "the same size". What does it tell us about the size of infinite sets?
Consider the sets A = { 1, 2, 3, ... }, the set of positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and B = { 2, 4, 6, ... }, the set of even positive integers. We claim that, under our definition, these sets have the same size, and that therefore B is countably infinite. Recall that to prove this we need to exhibit a bijection between them. But this is easy, using n ↔ 2n, so that
- 1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....
As in the earlier example, every element of A has been paired off with precisely one element of B, and vice versa. Hence they have the same size. This gives an example of a set which is of the same size as one of its proper subsets, a situation which is impossible for finite sets.
Likewise, the set of all ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of natural numbers is countably infinite, as can be seen by following a path like the one in the picture:

- 0 ↔ (0,0), 1 ↔ (1,0), 2 ↔ (0,1), 3 ↔ (2,0), 4 ↔ (1,1), 5 ↔ (0,2), 6 ↔ (3,0) ....
It is evident that this mapping will cover all such ordered pairs.
Interestingly: if you treat each pair as being the numerator and denominator of a vulgar fraction, then for every positive fraction, we can come up with a distinct number corresponding to it. This representation includes also the natural numbers, since every natural number is also a fraction N/1. So we can conclude that there are exactly as many positive rational numbers as there are positive integers. This is true also for all rational numbers, as can be seen below (a more complex presentation is needed to deal with negative numbers).
Theorem: The Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of finitely many countable sets is countable.
This form of triangular mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
generalizes to vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of finitely many natural numbers by repeatedly mapping the first two elements to a natural number. For example, (0,2,3) maps to (5,3) which maps to 39.
Sometimes more than one mapping is useful. This is where you map the set which you want to show countably infinite, onto another set; and then map this other set to the natural numbers. For example, the positive rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s can easily be mapped to (a subset of) the pairs of natural numbers because p/q maps to (p, q).
What about infinite subsets of countably infinite sets? Do these have fewer elements than N?
Theorem: Every subset of a countable set is countable. In particular, every infinite subset of a countably infinite set is countably infinite.
For example, the set of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s is countable, by mapping the n-th prime number to n:
- 2 maps to 1
- 3 maps to 2
- 5 maps to 3
- 7 maps to 4
- 11 maps to 5
- 13 maps to 6
- 17 maps to 7
- 19 maps to 8
- 23 maps to 9
- etc.
What about sets being "larger than" N? An obvious place to look would be Q, the set of all rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, which intuitively may seem much bigger than N. But looks can be deceiving, for we assert:
Theorem: Q (the set of all rational numbers) is countable.
Q can be defined as the set of all fractions a/b where a and b are integers and b > 0. This can be mapped onto the subset of ordered triples of natural numbers (a, b, c) such that a ≥ 0, b > 0, a and b are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, and c ∈ {0, 1} such that c = 0 if a/b ≥ 0 and c = 1 otherwise.
- 0 maps to (0,1,0)
- 1 maps to (1,1,0)
- −1 maps to (1,1,1)
- 1/2 maps to (1,2,0)
- −1/2 maps to (1,2,1)
- 2 maps to (2,1,0)
- −2 maps to (2,1,1)
- 1/3 maps to (1,3,0)
- −1/3 maps to (1,3,1)
- 3 maps to (3,1,0)
- −3 maps to (3,1,1)
- 1/4 maps to (1,4,0)
- −1/4 maps to (1,4,1)
- 2/3 maps to (2,3,0)
- −2/3 maps to (2,3,1)
- 3/2 maps to (3,2,0)
- −3/2 maps to (3,2,1)
- 4 maps to (4,1,0)
- −4 maps to (4,1,1)
- ...
By a similar development, the set of algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s is countable, and so is the set of definable number
Definable number
A real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
s.
Theorem: (Assuming the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
) The union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of countably many countable sets is countable.
For example, given countable sets a, b, c ...
Using a variant of the triangular enumeration we saw above:
- a0 maps to 0
- a1 maps to 1
- b0 maps to 2
- a2 maps to 3
- b1 maps to 4
- c0 maps to 5
- a3 maps to 6
- b2 maps to 7
- c1 maps to 8
- d0 maps to 9
- a4 maps to 10
- ...
Note that this only works if the sets a, b, c,... are disjoint. If not, then the union is even smaller and is therefore also countable by a previous theorem.
Also note that the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
is needed in order to index all of the sets a, b, c,...
Theorem: The set of all finite-length sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of natural numbers is countable.
This set is the union of the length-1 sequences, the length-2 sequences, the length-3 sequences, each of which is a countable set (finite Cartesian product). So we are talking about a countable union of countable sets, which is countable by the previous theorem.
Theorem: The set of all finite subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the natural numbers is countable.
If you have a finite subset, you can order the elements into a finite sequence. There are only countably many finite sequences, so also there are only countably many finite subsets.
The following theorem gives equivalent formulations in terms of a bijective function or a surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
. A proof of this result can be found in Lang's text.
Theorem: Let S be a set. The following statements are equivalent:
- S is countable, i.e. there exists an injective function
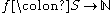 .
.
- Either S is empty or there exists a surjective function
 .
.
- Either S is finite or there exists a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
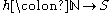 .
.
Several standard properties follow easily from this theorem. We present them here tersely. For a gentler presentation see the sections above. Observe that
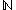 in the theorem can be replaced with any countably infinite set. In particular we have the following Corollary.
in the theorem can be replaced with any countably infinite set. In particular we have the following Corollary.Corollary: Let S and T be sets.
- If the function
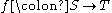 is injective and T is countable then S is countable.
is injective and T is countable then S is countable.
- If the function
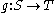 is surjective and S is countable then T is countable.
is surjective and S is countable then T is countable.
Proof: For (1) observe that if T is countable there is an injective function
 Then if
Then if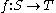 is injective
is injectivethe composition
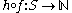 is injective, so S is countable.
is injective, so S is countable.For (2) observe that if S is countable there is a surjective function
 Then if
Then if 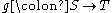 is surjective the composition
is surjective the composition  is surjective, so T is countable.
is surjective, so T is countable.Proposition: Any subset of a countable set is countable.
Proof: The restriction of an injective function to a subset of its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is still injective.
Proposition: The Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two countable sets A and B is countable.
Proof: Note that
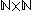 is countable as a consequence of the definition because the function
is countable as a consequence of the definition because the function 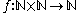 given by
given by 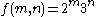 is injective. It then follows from the Basic Theorem and the Corollary that the Cartesian product of any two countable sets is countable. This follows because if A and B are countable there are surjections
is injective. It then follows from the Basic Theorem and the Corollary that the Cartesian product of any two countable sets is countable. This follows because if A and B are countable there are surjections 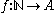 and
and 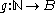 . So
. So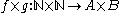
is a surjection from the countable set
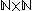 to the set
to the set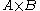 and the Corollary implies
and the Corollary implies 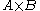 is countable. This result generalizes to the Cartesian product of any finite collection of countable sets and the proof follows by induction
is countable. This result generalizes to the Cartesian product of any finite collection of countable sets and the proof follows by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on the number of sets in the collection.
Proposition: The integers
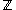 are countable and the rational numbers
are countable and the rational numbers 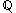 are countable.
are countable.Proof: The integers
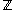 are countable because the function
are countable because the function 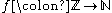 given by
given by 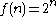 if n is non-negative and
if n is non-negative and 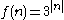 if n is negative is an injective function. The rational numbers
if n is negative is an injective function. The rational numbers 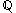 are countable because the function
are countable because the function 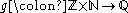 given by
given by 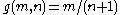 is a surjection from the countable set
is a surjection from the countable set  to the rationals
to the rationals 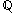 .
.Proposition: If
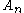 is a countable set for each
is a countable set for each 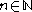 then
then  is countable.
is countable.Proof: This is a consequence of the fact that for each n there is a surjective function
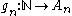 and hence the function
and hence the function
given by
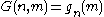 is a surjection. Since
is a surjection. Since 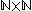 is countable the Corollary implies
is countable the Corollary implies  is countable. We are using the axiom of countable choice
is countable. We are using the axiom of countable choiceAxiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
in this proof in order to pick for each
 a surjection
a surjection 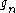 from the non-empty collection of surjections from
from the non-empty collection of surjections from 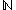 to
to  .
.Cantor's Theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
asserts that if
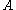 is a set and
is a set and  is its power set, i.e. the set of all subsets of
is its power set, i.e. the set of all subsets of 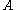 , then there is no surjective function from
, then there is no surjective function from 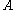 to
to  . A proof is given in the article Cantor's Theorem
. A proof is given in the article Cantor's TheoremCantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
. As an immediate consequence of this and the Basic Theorem above we have:
Proposition: The set
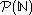 is not countable; i.e. it is uncountable.
is not countable; i.e. it is uncountable.For an elaboration of this result see Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
.
The set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is uncountable (see Cantor's first uncountability proof
Cantor's first uncountability proof
Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
), and so is the set of all infinite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of natural numbers. A topological proof for the uncountability of the real numbers is described at finite intersection property
Finite intersection property
In general topology, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty....
.
Minimal model of set theory is countable
If there is a set which is a standard model (see inner modelInner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
) of ZFC set theory, then there is a minimal standard model (see Constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
). The Löwenheim-Skolem theorem can be used to show that this minimal model is countable. The fact that the notion of "uncountability" makes sense even in this model, and in particular that this model M contains elements which are
- subsets of M, hence countable,
- but uncountable from the point of view of M,
was seen as paradoxical in the early days of set theory, see Skolem's paradox
Skolem's paradox
In mathematical logic and philosophy, Skolem's paradox is a seeming contradiction that arises from the downward Löwenheim–Skolem theorem. Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as...
.
The minimal standard model includes all the algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s and all effectively computable transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s, as well as many other kinds of numbers.
Total orders
Countable sets can be totally orderedTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
in various ways, e.g.:
- Well orders (see also ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
):- The usual order of natural numbers
- The integers in the order 0, 1, 2, 3, .., −1, −2, −3, ..
- Other:
- The usual order of integers
- The usual order of rational numbers
See also
- Aleph numberAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
- CountingCountingCounting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
- Hilbert's paradox of the Grand HotelHilbert's paradox of the Grand HotelHilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...

