Problem of Apollonius - AbsoluteAstronomy.com

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

, Apollonius' problem is to construct circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

s that are tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

to three given circles in a plane (Figure 1). Apollonius of Perga

Apollonius of Perga

Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...

(ca. 262 190 BC) posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria

Pappus of Alexandria

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...

has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2) and each solution circle encloses or excludes the three given circles in a different way.

In the 16th century, Adriaan van Roomen

Adriaan van Roomen

Adriaan van Roomen , also known as Adrianus Romanus, was a Flemish mathematician.-Life:Van Roomen was born in Leuven, the son of Adriaan Van Roomen and Maria Van Den Daele. He became a professor, and then travelled extensively in Europe.After studying at the Jesuit College in Cologne, Roomen...

solved the problem using intersecting hyperbola

Hyperbola

In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

s, but this solution does not use only straightedge and compass constructions. François Viète

François Viète

François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...

found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

(a point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

) or expanded to infinite radius (a line

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN

LORAN

LORAN is a terrestrial radio navigation system using low frequency radio transmitters in multiple deployment to determine the location and speed of the receiver....

.

Later mathematicians introduced algebraic methods

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

, which transform a geometric problem into algebraic equations. These methods were simplified by exploiting symmetries

Symmetry in mathematics

Symmetry occurs not only in geometry, but also in other branches of mathematics. It is actually the same as invariance: the property that something does not change under a set of transformations....

inherent in the problem of Apollonius: for instance solution circles generically occur in pairs, with one solution enclosing the given circles that the other excludes (Figure 2). Joseph Diaz Gergonne

Joseph Diaz Gergonne

Joseph Diaz Gergonne was a French mathematician and logician.-Life:In 1791, Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion because the French government feared a foreign invasion intended to undo the French Revolution and restore Louis XVI to full power...

used this symmetry to provide an elegant straightedge and compass solution, while other mathematicians used geometrical transformations such as reflection in a circle to simplify the configuration of the given circles. These developments provide a geometrical setting for algebraic methods (using Lie sphere geometry

Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century...

) and a classification of solutions according to 33 essentially different configurations of the given circles.

Apollonius' problem has stimulated much further work. Generalizations to three dimensions—constructing a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

tangent to four given spheres—and beyond have been studied. The configuration of three mutually tangent circles has received particular attention. René Descartes

René Descartes

René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...

gave a formula relating the radii of the solution circles and the given circles, now known as Descartes' theorem

Descartes' theorem

In geometry, Descartes' theorem, named after René Descartes, establishes a relationship between four kissing, or mutually tangent, circles. The theorem can be used to construct a fourth circle tangent to three given, mutually tangent circles.-History:...

. Solving Apollonius' problem iteratively in this case leads to the Apollonian gasket

Apollonian gasket

In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...

, which is one of the earliest fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

s to be described in print, and is important in number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

via Ford circles and the Hardy–Littlewood circle method.

Statement of the problem

The general statement of Apollonius' problem is to construct one or more circles that are tangent to three given objects in a plane, where an object may be a line, a point or a circle of any size. These objects may be arranged in any way and may cross one another; however, they are usually taken to be distinct, meaning that they do not coincide. Solutions to Apollonius' problem are sometimes called Apollonius circles, although the term is also used for other types of circles

Circles of Apollonius

The term circle of Apollonius is used to describe several types of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a...

associated with Apollonius.

The property of tangency is defined as follows. First, a point, line or circle is assumed to be tangent to itself; hence, if a given circle is already tangent to the other two given objects, it is counted as a solution to Apollonius' problem. Two distinct geometrical objects are said to intersect if they have a point in common. By definition, a point is tangent to a circle or a line if it intersects them, that is, if it lies on them; thus, two distinct points cannot be tangent. If the angle between lines or circles at an intersection point is zero, they are said to be tangent; the intersection point is called a tangent point or a point of tangency. (The word "tangent" derives from the Latin

Latin

Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...

present participle

Participle

In linguistics, a participle is a word that shares some characteristics of both verbs and adjectives. It can be used in compound verb tenses or voices , or as a modifier...

, tangens, meaning "touching".) In practice, two distinct circles are tangent if they intersect at only one point; if they intersect at zero or two points, they are not tangent. The same holds true for a line and a circle. Two distinct lines cannot be tangent in the plane, although two parallel

Parallel (geometry)

Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...

lines can be considered as tangent at a point at infinity in inversive geometry (see below).

The solution circle may be either internally or externally tangent to each of the given circles. An external tangency is one where the two circles bend away from each other at their point of contact; they lie on opposite sides of the tangent line

Tangent lines to circles

In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...

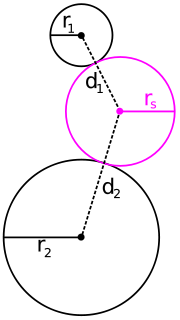
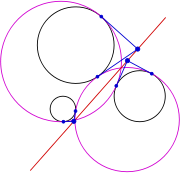
at that point, and they exclude one another. The distance between their centers equals the sum of their radii. By contrast, an internal tangency is one in which the two circles curve in the same way at their point of contact; the two circles lie on the same side of the tangent line, and one circle encloses the other. In this case, the distance between their centers equals the difference of their radii. As an illustration, in Figure 1, the pink solution circle is internally tangent to the medium-sized given black circle on the right, whereas it is externally tangent to the smallest and largest given circles on the left.

Apollonius' problem can also be formulated as the problem of locating one or more points such that the differences of its distances to three given points equal three known values. Consider a solution circle of radius r_s and three given circles of radii r₁, r₂ and r₃. If the solution circle is externally tangent to all three given circles, the distances between the center of the solution circle and the centers of the given circles equal , and , respectively. Therefore, differences in these distances are constants, such as ; they depend only on the known radii of the given circles and not on the radius r_s of the solution circle, which cancels out. This second formulation of Apollonius' problem can be generalized to internally tangent solution circles (for which the center-center distance equals the difference of radii), by changing the corresponding differences of distances to sums of distances, so that the solution-circle radius r_s again cancels out. The re-formulation in terms of center-center distances is useful in the solutions below of Adriaan van Roomen

Adriaan van Roomen

and Isaac Newton

Isaac Newton

, and also in hyperbolic positioning or trilateration, which is the task of locating a position from differences in distances to three known points. For example, navigation systems such as LORAN

LORAN

LORAN is a terrestrial radio navigation system using low frequency radio transmitters in multiple deployment to determine the location and speed of the receiver....

identify a receiver's position from the differences in arrival times of signals from three fixed positions, which correspond to the differences in distances to those transmitters.

History

A rich repertoire of geometrical and algebraic methods have been developed to solve Apollonius' problem, which has been called "the most famous of all" geometry problems. The original approach of Apollonius of Perga

Apollonius of Perga

has been lost, but reconstructions have been offered by François Viète

François Viète

and others, based on the clues in the description by Pappus

Pappus of Alexandria

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...

. The first new solution method was published in 1596 by Adriaan van Roomen

Adriaan van Roomen

, who identified the centers of the solution circles as the intersection points of two hyperbola

Hyperbola

s. Van Roomen's method was refined in 1687 by Isaac Newton

Isaac Newton

in his Principia, and by John Casey

John Casey (mathematician)

John Casey was a respected Irish geometer. He is most famous for Casey's theorem on a circle that is tangent to four other circles, an extension of the problem of Apollonius. However, he contributed several novel proofs and perspectives on Euclidean geometry...

in 1881.

Although successful in solving Apollonius' problem, van Roomen's method has a drawback. A prized property in classical Euclidean geometry

Euclidean geometry

is the ability to solve problems using only a compass and a straightedge. Many constructions are impossible using only these tools, such as dividing an angle in three equal parts

Angle trisection

Angle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....

. However, many such "impossible" problems can be solved by intersecting curves such as hyperbolas, ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

s and parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

s (conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

s). For example, doubling the cube

Doubling the cube

Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...

(the problem of constructing a cube of twice the volume of a given cube) cannot be done using only a straightedge and compass, but Menaechmus

Menaechmus

Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube...

showed that the problem can be solved by using the intersections of two parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

s. Therefore, van Roomen's solution—which uses the intersection of two hyperbolas—did not determine if the problem satisfied the straightedge-and-compass property.

Van Roomen's friend François Viète

François Viète

, who had urged van Roomen to work on Apollonius' problem in the first place, developed a method that used only compass and straightedge. Prior to Viète's solution, Regiomontanus

Regiomontanus

Johannes Müller von Königsberg , today best known by his Latin toponym Regiomontanus, was a German mathematician, astronomer, astrologer, translator and instrument maker....

doubted whether Apollonius' problem could be solved by straightedge and compass. Viète first solved some simple special cases of Apollonius' problem, such as finding a circle that passes through three given points which has only one solution if the points are distinct; he then built up to solving more complicated special cases, in some cases by shrinking or swelling the given circles. According to the 4th-century report of Pappus of Alexandria

Pappus of Alexandria

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...

, Apollonius' own book on this problem—entitled —followed a similar progressive approach. Hence, Viète's solution is considered to be a plausible reconstruction of Apollonius' solution, although other reconstructions have been published independently by three different authors.

Several other geometrical solutions to Apollonius' problem were developed in the 19th century. The most notable solutions are those of Jean-Victor Poncelet

Jean-Victor Poncelet

Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...

(1811) and of Joseph Diaz Gergonne

Joseph Diaz Gergonne

(1814). Whereas Poncelet's proof relies on homothetic centers of circles and the power of a point

Power of a point

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...

theorem, Gergonne's method exploits the conjugate relation between lines and their poles in a circle. Methods using circle inversion were pioneered by Julius Petersen

Julius Petersen

Julius Peter Christian Petersen was a Danish mathematician.-Biography:Petersen's interests in mathematics were manifold .His famous paper Die Theorie der regulären graphs was a fundamental...

in 1879; one example is the annular solution method of HSM Coxeter

Harold Scott MacDonald Coxeter

Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....

. Another approach uses Lie sphere geometry

Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century...

, which was developed by Sophus Lie

Sophus Lie

Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...

.

Algebraic solutions to Apollonius' problem were pioneered in the 17th century by René Descartes

René Descartes

and Princess Elisabeth of Bohemia

Elisabeth of Bohemia, Princess Palatine

Elisabeth of the Palatinate , also known as Elisabeth of Bohemia, was the eldest daughter of Frederick V, who was briefly elected King of Bohemia, and Elizabeth Stuart. She ruled the Herford Abbey as Princess-Abbess Elizabeth III...

, although their solutions were rather complex. Practical algebraic methods were developed in the late 18th and 19th centuries by several mathematicians, including Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

, Nicolas Fuss

Nicolas Fuss

Nicolas Fuss , also known as Nikolai Fuss, was a Swiss mathematician.Fuss was born in Basel, Switzerland. He moved to Saint Petersburg to serve as a mathematical assistant to Leonhard Euler from 1773–1783, and remained there until his death...

, Carl Friedrich Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

, Lazare Carnot

Lazare Carnot

Lazare Nicolas Marguerite, Comte Carnot , the Organizer of Victory in the French Revolutionary Wars, was a French politician, engineer, and mathematician.-Education and early life:...

, and Augustin Louis Cauchy

Augustin Louis Cauchy

Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...

Intersecting hyperbolas

The solution of Adriaan van Roomen

Adriaan van Roomen

(1596) is based on the intersection of two hyperbola

Hyperbola

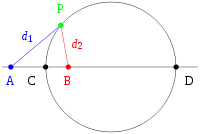
s. Let the given circles be denoted as C₁, C₂ and C₃. Van Roomen solved the general problem by solving a simpler problem, that of finding the circles that are tangent to two given circles, such as C₁ and C₂. He noted that the center of a circle tangent to both given circles must lie on a hyperbola

Hyperbola

whose foci are the centers of the given circles. To understand this, let the radii of the solution circle and the two given circles be denoted as r_s, r₁ and r₂, respectively (Figure 3). The distance d₁ between the centers of the solution circle and C₁ is either or , depending on whether these circles are chosen to be externally or internally tangent, respectively. Similarly, the distance d₂ between the centers of the solution circle and C₂ is either or , again depending on their chosen tangency. Thus, the difference between these distances is always a constant that is independent of r_s. This property, of having a fixed difference between the distances to the foci

Focus (geometry)

In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...

, characterizes hyperbolas, so the possible centers of the solution circle lie on a hyperbola. A second hyperbola can be drawn for the pair of given circles C₂ and C₃, where the internal or external tangency of the solution and C₂ should be chosen consistently with that of the first hyperbola. An intersection of these two hyperbolas (if any) gives the center of a solution circle that has the chosen internal and external tangencies to the three given circles. The full set of solutions to Apollonius' problem can be found by considering all possible combinations of internal and external tangency of the solution circle to the three given circles.

Isaac Newton

Isaac Newton

(1687) refined van Roomen's solution, so that the solution-circle centers were located at the intersections of a line with a circle. Newton formulates Apollonius' problem as a problem in trilateration

Trilateration

In geometry, trilateration is the process of determinating absolute or relative locations of points by measurement of distances, using the geometry of circles, spheres or triangles. In addition to its interest as a geometric problem, trilateration does have practical applications in surveying and...

: to locate a point Z from three given points A, B and C, such that the differences in distances from Z to the three given points have known values. These four points correspond to the center of the solution circle (Z) and the centers of the three given circles (A, B and C).

Instead of solving for the two hyperbolas, Newton constructs their directrix lines

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

instead. For any hyperbola, the ratio of distances from a point Z to a focus A and to the directrix is a fixed constant called the eccentricity

Eccentricity (mathematics)

In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...

. The two directrices intersect at a point T, and from their two known distance ratios, Newton constructs a line passing through T on which Z must lie. However, the ratio of distances TZ/TA is also known; hence, Z also lies on a known circle, since Apollonius had shown that a circle

Circle

can be defined as the set of points that have a given ratio of distances to two fixed points. (As an aside, this definition is the basis of bipolar coordinates

Bipolar coordinates

Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...

.) Thus, the solutions to Apollonius' problem are the intersections of a line with a circle.

Viète's reconstruction

As described below, Apollonius' problem has ten special cases, depending on the nature of the three given objects, which may be a circle (C), line (L) or point (P). By custom, these ten cases are distinguished by three letter codes such as CCP. Viète solved all ten of these cases using only compass and straightedge constructions, and used the solutions of simpler cases to solve the more complex cases.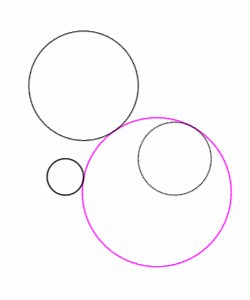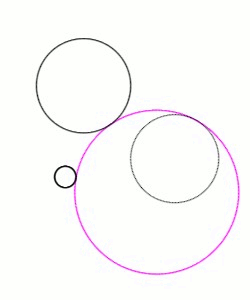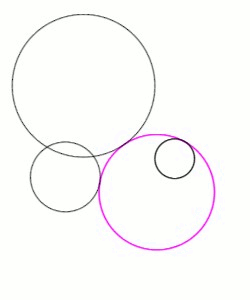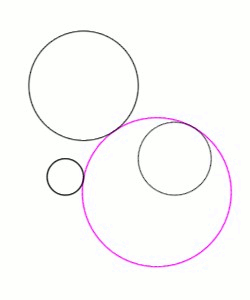

Viète began by solving the PPP case (three points) following the method of Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

in his Elements

Euclid's Elements

Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...

. From this, he derived a lemma

Lemma (mathematics)

In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...

corresponding to the power of a point

Power of a point

theorem, which he used to solve the LPP case (a line and two points). Following Euclid a second time, Viète solved the LLL case (three lines) using the angle bisectors

Angle bisector theorem

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.Consider a triangle...

. He then derived a lemma for constructing the line perpendicular to an angle bisector that passes through a point, which he used to solve the LLP problem (two lines and a point). This accounts for the first four cases of Apollonius' problem, those that do not involve circles.

To solve the remaining problems, Viète exploited the fact that the given circles and the solution circle may be re-sized in tandem while preserving their tangencies (Figure 4). If the solution-circle radius is changed by an amount Δr, the radius of its internally tangent given circles must be likewise changed by Δr, whereas the radius of its externally tangent given circles must be changed by −Δr. Thus, as the solution circle swells, the internally tangent given circles must swell in tandem, whereas the externally tangent given circles must shrink, to maintain their tangencies.

Viète used this approach to shrink one of the given circles to a point, thus reducing the problem to a simpler, already solved case. He first solved the CLL case (a circle and two lines) by shrinking the circle into a point, rendering it a LLP case. He then solved the CLP case (a circle, a line and a point) using three lemmas. Again shrinking one circle to a point, Viète transformed the CCL case into a CLP case. He then solved the CPP case (a circle and two points) and the CCP case (two circles and a point), the latter case by two lemmas. Finally, Viète solved the general CCC case (three circles) by shrinking one circle to a point, rendering it a CCP case.

Algebraic solutions

Apollonius' problem can be framed as a system of three equations for the center and radius of the solution circle. Since the three given circles and any solution circle must lie in the same plane, their positions can be specified in terms of the (x, y) coordinates

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

of their centers. For example, the center positions of the three given circles may be written as (x₁, y₁), (x₂, y₂) and (x₃, y₃), whereas that of a solution circle can be written as (x_s, y_s). Similarly, the radii of the given circles and a solution circle can be written as r₁, r₂, r₃ and r_s, respectively. The requirement that a solution circle must exactly touch each of the three given circles can be expressed as three coupled quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

s for x_s, y_s and r_s:

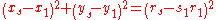
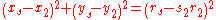
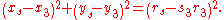
The three numbers s₁, s₂ and s₃ on the right-hand side

Sides of an equation

In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. Each is solely a name for a term as part of an expression; and they are in practice interchangeable, since equality is symmetric...

, called signs, may equal ±1, and specify whether the desired solution circle should touch the corresponding given circle internally (s = 1) or externally (s = −1). For example, in Figures 1 and 4, the pink solution is internally tangent to the medium-sized given circle on the right and externally tangent to the smallest and largest given circles on the left; if the given circles are ordered by radius, the signs for this solution are . Since the three signs may be chosen independently, there are eight possible sets of equations , each set corresponding to one of the eight types of solution circles.

The general system of three equations may be solved by the method of resultants. When multiplied out, all three equations have on the left-hand side, and r_s² on the right-hand side. Subtracting one equation from another eliminates these quadratic terms; the remaining linear terms may be re-arranged to yield formulae for the coordinates x_s and y_s

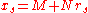
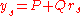
where M, N, P and Q are known functions of the given circles and the choice of signs. Substitution of these formulae into one of the initial three equations gives a quadratic equation for r_s, which can be solved by the quadratic formula. Substitution of the numerical value of r_s into the linear formulae yields the corresponding values of x_s and y_s.

The signs s₁, s₂ and s₃ on the right-hand sides of the equations may be chosen in eight possible ways, and each choice of signs gives up to two solutions, since the equation for r_s is quadratic

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

. This might suggest (incorrectly) that there are up to sixteen solutions of Apollonius' problem. However, due to a symmetry of the equations, if (r_s, x_s, y_s) is a solution, with signs s_i, then so is (−r_s, x_s, y_s), with opposite signs −s_i, which represents the same solution circle. Therefore, Apollonius' problem has at most eight independent solutions (Figure 2). One way to avoid this double-counting is to consider only solution circles with non-negative radius.

The two roots of any quadratic equation may be of three possible types: two different real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, two identical real numbers (i.e., a degenerate double root), or a pair of complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

roots. The first case corresponds to the usual situation; each pair of roots corresponds to a pair of solutions that are related by circle inversion, as described below (Figure 6). In the second case, both roots are identical, corresponding to a solution circle that transforms into itself under inversion. In this case, one of the given circles is itself a solution to the Apollonius problem, and the number of distinct solutions is reduced by one. The third case of complex conjugate radii does not correspond to a geometrically possible solution for Apollonius' problem, since a solution circle cannot have an imaginary radius; therefore, the number of solutions is reduced by two. Interestingly, Apollonius' problem cannot have seven solutions, although it may have any other number of solutions from zero to eight.

Lie sphere geometry

The same algebraic equations can be derived in the context of Lie sphere geometry

Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century...

. That geometry represents circles, lines and points in a unified way, as a five-dimensional vector X = (v, c_x, c_y, w, sr), where c = (c_x, c_y) is the center of the circle, and r is its (non-negative) radius. If r is not zero, the sign s may be positive or negative; for visualization, s represents the orientation

Curve orientation

In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...

of the circle, with counterclockwise circles having a positive s and clockwise circles having a negative s. The parameter w is zero for a straight line, and one otherwise.

In this five-dimensional world, there is a bilinear product similar to the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

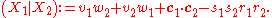
The Lie quadric is defined as those vectors whose product with themselves (their square norm

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

) is zero, (X|X) = 0. Let X₁ and X₂ be two vectors belonging to this quadric; the norm of their difference equals

The product distributes

Distributivity

In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...

over addition and subtraction (more precisely, it is bilinear):

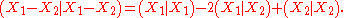
Since (X₁|X₁) = (X₂|X₂) = 0 (both belong to the Lie quadric) and since w₁ = w₂ = 1 for circles, the product of any two such vectors on the quadric equals

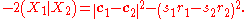
where the vertical bars sandwiching represent the length of that difference vector, i.e., the Euclidean norm. This formula shows that if two quadric vectors X₁ and X₂ are orthogonal (perpendicular) to one another—that is, if (X₁|X₂)=0—then their corresponding circles are tangent. For if the two signs s₁ and s₂ are the same (i.e. the circles have the same "orientation"), the circles are internally tangent; the distance between their centers equals the difference in the radii

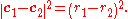
Conversely, if the two signs s₁ and s₂ are different (i.e. the circles have opposite "orientations"), the circles are externally tangent; the distance between their centers equals the sum of the radii

Therefore, Apollonius' problem can be re-stated in Lie geometry as a problem of finding perpendicular vectors on the Lie quadric; specifically, the goal is to identify solution vectors X_sol that belong to the Lie quadric and are also orthogonal (perpendicular) to the vectors X₁, X₂ and X₃ corresponding to the given circles.

The advantage of this re-statement is that one can exploit theorems from linear algebra

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

on the maximum number of linearly independent, simultaneously perpendicular vectors. This gives another way to calculate the maximum number of solutions and extend the theorem to higher dimensional spaces.

Inversive methods

A natural setting for problem of Apollonius is inversive geometry. The basic strategy of inversive methods is to transform a given Apollonius problem into another Apollonius problem that is simpler to solve; the solutions to the original problem are found from the solutions of the transformed problem by undoing the transformation. Candidate transformations must change one Apollonius problem into another; therefore, they must transform the given points, circles and lines to other points, circles and lines, and no other shapes. Circle inversion has this property and allows the center and radius of the inversion circle to be chosen judiciously. Other candidates include the Euclidean plane isometries

Euclidean plane isometry

In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length...

; however, they do not simplify the problem, since they merely shift, rotate, and mirror

Reflection (mathematics)

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

the original problem.

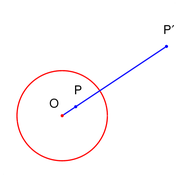
Inversion in a circle with center O and radius R consists of the following operation (Figure 5): every point P is mapped into a new point P' such that O, P, and P' are collinear, and the product of the distances of P and P' to the center O equal the radius R squared

Thus, if P lies outside the circle, then P' lies within, and vice versa. When P is the same as O, the inversion is said to send P to infinity. (In complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, "infinity" is defined in terms of the Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

.) Inversion has the useful property that lines and circles are always transformed into lines and circles, and points are always transformed into points. Circles are generally transformed into other circles under inversion; however, if a circle passes through the center of the inversion circle, it is transformed into a straight line, and vice versa. Importantly, if a circle crosses the circle of inversion at right angles (intersects perpendicularly), it is left unchanged by the inversion; it is transformed into itself.

Circle inversions correspond to a subset of Möbius transformations on the Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

. The planar Apollonius problem can be transferred to the sphere by an inverse stereographic projection

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

; hence, solutions of the planar Apollonius problem also pertain to its counterpart on the sphere. Other inversive solutions to the planar problem are possible besides the common ones described below.

Pairs of solutions by inversion

Solutions to Apollonius' problem generally occur in pairs; for each solution circle, there is a conjugate solution circle (Figure 6). One solution circle excludes the given circles that are enclosed by its conjugate solution, and vice versa. For example, in Figure 6, one solution circle (pink, upper left) encloses two given circles (black), but excludes a third; conversely, its conjugate solution (also pink, lower right) encloses that third given circle, but excludes the other two. The two conjugate solution circles are related by inversion, by the following argument.

In general, any three distinct circles have a unique circle—the radical circle—that intersects all of them perpendicularly; the center of that circle is the radical center of the three circles. For illustration, the orange circle in Figure 6 crosses the black given circles at right angles. Inversion in the radical circle leaves the given circles unchanged, but transforms the two conjugate pink solution circles into one another. Under the same inversion, the corresponding points of tangency of the two solution circles are transformed into one another; for illustration, in Figure 6, the two blue points lying on each green line are transformed into one another. Hence, the lines connecting these conjugate tangent points are invariant under the inversion; therefore, they must pass through the center of inversion, which is the radical center (green lines intersecting at the orange dot in Figure 6).

Inversion to an annulus

If two of the three given circles do not intersect, a center of inversion can be chosen so that those two given circles become concentric

Concentric

Concentric objects share the same center, axis or origin with one inside the other. Circles, tubes, cylindrical shafts, disks, and spheres may be concentric to one another...

. Under this inversion, the solution circles must fall within the annulus

Annulus (mathematics)

In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...

between the two concentric circles. Therefore, they belong to two one-parameter families. In the first family (Figure 7), the solutions do not enclose the inner concentric circle, but rather revolve like ball bearings in the annulus. In the second family (Figure 8), the solution circles enclose the inner concentric circle. There are generally four solutions for each family, yielding eight possible solutions, consistent with the algebraic solution.

When two of the given circles are concentric, Apollonius' problem can be solved easily using a method of Gauss

Carl Friedrich Gauss

. The radii of the three given circles are known, as is the distance d_non from the common concentric center to the non-concentric circle (Figure 7). The solution circle can be determined from its radius r_s, the angle θ, and the distances d_s and d_T from its center to the common concentric center and the center of the non-concentric circle, respectively. The radius and distance d_s are known (Figure 7), and the distance d_T = r_s ± r_non, depending on whether the solution circle is internally or externally tangent to the non-concentric circle. Therefore, by the law of cosines

Law of cosines

In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...

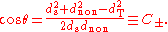
Here, a new constant C has been defined for brevity, with the subscript indicating whether the solution is externally or internally tangent. A simple trigonometric rearrangement yields the four solutions

This formula represents four solutions, corresponding to the two choices of the sign of θ, and the two choices for C. The remaining four solutions can be obtained by the same method, using the substitutions for r_s and d_s indicated in Figure 8. Thus, all eight solutions of the general Apollonius problem can be found by this method.

Any initial two disjoint given circles can be rendered concentric as follows. The radical axis

Radical axis

The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...

of the two given circles is constructed; choosing two arbitrary points P and Q on this radical axis, two circles can be constructed that are centered on P and Q and that intersect the two given circles orthogonally. These two constructed circles intersect each other in two points. Inversion in one such intersection point F renders the constructed circles into straight lines emanating from F and the two given circles into concentric circles, with the third given circle becoming another circle (in general). This follows because the system of circles is equivalent to a set of Apollonian circles

Apollonian circles

Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...

, forming a bipolar coordinate system.

Resizing and inversion

The usefulness of inversion can be increased significantly by resizing. As noted in Viète's reconstruction, the three given circles and the solution circle can be resized in tandem while preserving their tangencies. Thus, the initial Apollonius problem is transformed into another problem that may be easier to solve. For example, the four circles can be resized so that one given circle is shrunk to a point; alternatively, two given circles can often be resized so that they are tangent to one another. Thirdly, given circles that intersect can be resized so that they become non-intersecting, after which the method for inverting to an annulus can be applied. In all such cases, the solution of the original Apollonius problem is obtained from the solution of the transformed problem by undoing the resizing and inversion.

Shrinking one given circle to a point

In the first approach, the given circles are shrunk or swelled (appropriately to their tangency) until one given circle is shrunk to a point P. In that case, Apollonius' problem degenerates to the CCP limiting case, which is the problem of finding a solution circle tangent to the two remaining given circles that passes through the point P. Inversion in a circle centered on P transforms the two given circles into new circles, and the solution circle into a line. Therefore, the transformed solution is a line that is tangent to the two transformed given circles. There are four such solution lines, which may be constructed from the external and internal homothetic center

Homothetic center

In geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation/contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense...

s of the two circles. Re-inversion in P and undoing the resizing transforms such a solution line into the desired solution circle of the original Apollonius problem. All eight general solutions can be obtained by shrinking and swelling the circles according to the differing internal and external tangencies of each solution; however, different given circles may be shrunk to a point for different solutions.

Resizing two given circles to tangency

In the second approach, the radii of the given circles are modified appropriately by an amount Δr so that two of them are tangential (touching). Their point of tangency is chosen as the center of inversion in a circle that intersects each of the two touching circles in two places. Upon inversion, the touching circles become two parallel lines: Their only point of intersection is sent to infinity under inversion, so they cannot meet. The same inversion transforms the third circle into another circle. The solution of the inverted problem must either be (1) a straight line parallel to the two given parallel lines and tangent to the transformed third given circle; or (2) a circle of constant radius that is tangent to the two given parallel lines and the transformed given circle. Re-inversion and adjusting the radii of all circles by Δr produces a solution circle tangent to the original three circles.

Gergonne's solution

Gergonne's approach is to consider the solution circles in pairs. Let a pair of solution circles be denoted as C_A and C_B (the pink circles in Figure 6), and let their tangent points with the three given circles be denoted as A₁, A₂, A₃, and B₁, B₂, B₃, respectively. Gergonne's solution aims to locate these six points, and thus solve for the two solution circles.

Gergonne's insight was that if a line L₁ could be constructed such that A₁ and B₁ were guaranteed to fall on it, those two points could be identified as the intersection points of L₁ with the given circle C₁ (Figure 6). The remaining four tangent points would be located similarly, by finding lines L₂ and L₃ that contained A₂ and B₂, and A₃ and B₃, respectively. To construct a line such as L₁, two points must be identified that lie on it; but these points need not be the tangent points. Gergonne was able to identify two other points for each of the three lines. One of the two points has already been identified: the radical center G lies on all three lines (Figure 6).

To locate a second point on the lines L₁, L₂ and L₃, Gergonne noted a reciprocal relationship between those lines and the radical axis

Radical axis

R of the solution circles, C_A and C_B. To understand this reciprocal relationship, consider the two tangent lines to the circle C₁ drawn at its tangent points A₁ and B₁ with the solution circles; the intersection of these tangent lines is the pole point of L₁ in C₁. Since the distances from that pole point to the tangent points A₁ and B₁ are equal, this pole point must also lie on the radical axis R of the solution circles, by definition (Figure 9). The relationship between pole points and their polar lines is reciprocal; if the pole of L₁ in C₁ lies on R, the pole of R in C₁ must conversely lie on L₁. Thus, if we can construct R, we can find its pole P₁ in C₁, giving the needed second point on L₁ (Figure 10).

Gergonne found the radical axis R of the unknown solution circles as follows. Any pair of circles has two centers of similarity

Homothetic center

; these two points are the two possible intersections of two tangent lines to the two circles. Therefore, the three given circles have six centers of similarity, two for each distinct pair of given circles. Remarkably, these six points lie on four lines, three points on each line; moreover, each line corresponds to the radical axis

Radical axis

of a potential pair of solution circles. To show this, Gergonne considered lines through corresponding points of tangency on two of the given circles, e.g., the line defined by A₁/A₂ and the line defined by B₁/B₂. Let X₃ be a center of similitude for the two circles C₁ and C₂; then, A₁/A₂ and B₁/B₂ are pairs of antihomologous points, and their lines intersect at X₃. It follows, therefore, that the products of distances are equal

which implies that X₃ lies on the radical axis of the two solution circles. The same argument can be applied to the other pairs of circles, so that three centers of similitude for the given three circles must lie on the radical axes of pairs of solution circles.

In summary, the desired line L₁ is defined by two points: the radical center G of the three given circles and the pole in C₁ of one of the four lines connecting the homothetic centers. Finding the same pole in C₂ and C₃ gives L₂ and L₃, respectively; thus, all six points can be located, from which one pair of solution circles can be found. Repeating this procedure for the remaining three homothetic-center lines yields six more solutions, giving eight solutions in all. However, if a line L_k does not intersect its circle C_k for some k, there is no pair of solutions for that homothetic-center line.

Ten combinations of points, circles, and lines

Apollonius problem is to construct one or more circles tangent to three given objects in a plane, which may be circles, points, or lines. This gives rise to ten types of Apollonius' problem, one corresponding to each combination of circles, lines and points, which may be labeled with three letters, either C, L, or P, to denote whether the given elements are a circle, line or point, respectively (Table 1). As an example, the type of Apollonius problem with a given circle, line, and point is denoted as CLP.

Some of these special cases are much easier to solve than the general case of three given circles. The two simplest cases are the problems of drawing a circle through three given points (PPP) or tangent to three lines (LLL), which were solved first by Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

in his Elements

Euclid's Elements

. For example, the PPP problem can be solved as follows. The center of the solution circle is equally distant from all three points, and therefore must lie on the perpendicular bisector line of any two. Hence, the center is the point of intersection of any two perpendicular bisectors. Similarly, in the LLL case, the center must lie on a line bisecting the angle at the three intersection points between the three given lines; hence, the center lies at the intersection point of two such angle bisectors. Since there are two such bisectors at every intersection point of the three given lines, there are four solutions to the general LLL problem.

Points and lines may be viewed as special cases of circles; a point can be considered as a circle of infinitely small radius, and a line may be thought of an infinitely large circle whose center is also at infinity. From this perspective, the general Apollonius problem is that of constructing circles tangent to three given circles. The nine other cases involving points and lines may be viewed as limiting cases of the general problem. These limiting cases often have fewer solutions than the general problem; for example, the replacement of a given circle by a given point halves the number of solutions, since a point can be construed as an infinitesimal circle that is either internally or externally tangent.

Table 1: Ten Types of Apollonius' Problem
Index	Code	Given Elements	Number of solutions (in general)
1	PPP	three points	1
2	LPP	one line and two points	2
3	LLP	two lines and a point	2
4	CPP	one circle and two points	2
5	LLL	three lines	4
6	CLP	one circle, one line, and a point	4
7	CCP	two circles and a point	4
8	CLL	one circle and two lines	8
9	CCL	two circles and a line	8
10	CCC	three circles (the classic problem)	8

Number of solutions

The problem of counting the number of solutions to different types of Apollonius' problem belongs to the field of enumerative geometry

Enumerative geometry

In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.-History:...

. The general number of solutions for each of the ten types of Apollonius' problem is given in Table 1 above. However, special arrangements of the given elements may change the number of solutions. For illustration, Apollonius' problem has no solution if one circle separates the two (Figure 11); to touch both the solid given circles, the solution circle would have to cross the dashed given circle; but that it cannot do, if it is to touch the dashed circle tangentially. Conversely, if three given circles are all tangent at the same point, then any circle tangent at the same point is a solution; such Apollonius problems have an infinite number of solutions. If any of the given circles are identical, there is likewise an infinity of solutions. If only two given circles are identical, there are only two distinct given circles; the centers of the solution circles form a hyperbola

Hyperbola

, as used in one solution to Apollonius' problem.

An exhaustive enumeration of the number of solutions for all possible configurations of three given circles, points or lines was first undertaken by Muirhead in 1896, although earlier work had been done by Stoll and Study. However, Muirhead's work was incomplete; it was extended in 1974 and a definitive enumeration, with 33 distinct cases, was published in 1983. Although solutions to Apollonius' problem generally occur in pairs related by inversion, an odd number of solutions is possible in some cases, e.g., the single solution for PPP, or when one or three of the given circles are themselves solutions. (An example of the latter is given in the section on Descartes' theorem

Descartes' theorem

.) However, there are no Apollonius problems with seven solutions. Alternative solutions based on the geometry of circles and spheres

Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century...

have been developed and used in higher dimensions.

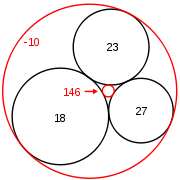
Mutually tangent given circles: Soddy's circles and Descartes' theorem

If the three given circles are mutually tangent, Apollonius' problem has five solutions. Three solutions are the given circles themselves, since each is tangent to itself and to the other two given circles. The remaining two solutions (shown in red in Figure 12) correspond to the inscribed

Incircle and excircles of a triangle

In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...

and circumscribed circle

Circumscribed circle

In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....

s, and are called Soddy's circles. This special case of Apollonius' problem is also known as the four coins problem. The three given circles of this Apollonius problem form a Steiner chain

Steiner chain

In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles , where n is finite and each circle in the chain is tangent to the previous and next circles in the chain...

tangent to the two Soddy's circles.

Either Soddy circle, when taken together with the three given circles, produces a set of four circles that are mutually tangent at six points. The radii of these four circles are related by an equation known as Descartes' theorem

Descartes' theorem

. In a 1643 letter to Princess Elizabeth of Bohemia

Elizabeth of Bohemia

Elizabeth of Bohemia was the eldest daughter of King James VI and I, King of Scotland, England, Ireland, and Anne of Denmark. As the wife of Frederick V, Elector Palatine, she was Electress Palatine and briefly Queen of Bohemia...

, René Descartes

René Descartes

showed that

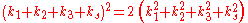
where k_s = 1/r_s and r_s are the curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

and radius of the solution circle, respectively, and similarly for the curvatures k₁, k₂ and k₃ and radii r₁, r₂ and r₃ of the three given circles. For every set of four mutually tangent circles, there is a second set of four mutually tangent circles that are tangent at the same six points.

Descartes' theorem was rediscovered independently in 1826 by Jakob Steiner

Jakob Steiner

Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...

, in 1842 by Philip Beecroft, and again in 1936 by Frederick Soddy

Frederick Soddy

Frederick Soddy was an English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. He also proved the existence of isotopes of certain radioactive elements...

. Soddy published his findings in the scientific journal Nature

Nature (journal)

Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...

as a poem, The Kiss Precise, of which the first two stanzas are reproduced below. The first stanza describes Soddy's circles, whereas the second stanza gives Descartes' theorem. In Soddy's poem, two circles are said to "kiss" if they are tangent, whereas the term "bend" refers to the curvature k of the circle.

For pairs of lips to kiss maybe

Involves no trigonometry.

Tis not so when four circles kiss

Each one the other three.

To bring this off the four must be

As three in one or one in three.

If one in three, beyond a doubt

Each gets three kisses from without.

If three in one, then is that one

Thrice kissed internally.

Four circles to the kissing come.

The smaller are the benter.

The bend is just the inverse of

The distance from the center.

Though their intrigue left Euclid dumb

There's now no need for rule of thumb.

Since zero bend's a dead straight line

And concave bends have minus sign,

The sum of the squares of all four bends

Is half the square of their sum.

Sundry extensions of Descartes' theorem have been derived by Daniel Pedoe

Daniel Pedoe

Dan Pedoe was an English-born mathematician and geometer with a career spanning more than sixty years. In the course of his life he wrote approximately fifty research and expository papers in geometry. He is also the author of various core books on mathematics and geometry some of which have...

Generalizations

Apollonius' problem can be extended to construct all the circles that intersect three given circles at a precise angle θ, or at three specified crossing angles θ₁, θ₂ and θ₃; the ordinary Apollonius' problem corresponds to a special case in which the crossing angle is zero for all three given circles. Another generalization is the dual

Duality (mathematics)

In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...

of the first extension, namely, to construct circles with three specified tangential distances from the three given circles.

Apollonius' problem can be extended from the plane to the sphere

Sphere

and other quadratic surfaces. For the sphere, the problem is to construct all the circles (the boundaries of spherical cap

Spherical cap

In geometry, a spherical cap is a portion of a sphere cut off by a plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere....

s) that are tangent to three given circles on the sphere. This spherical problem can be rendered into a corresponding planar problem using stereographic projection

Stereographic projection

. Once the solutions to the planar problem have been constructed, the corresponding solutions to the spherical problem can be determined by inverting the stereographic projection. Even more generally, one can consider the problem of four tangent curves that result from the intersections of an arbitrary quadratic surface and four planes, a problem first considered by Charles Dupin

Charles Dupin

Pierre Charles François Dupin was a French Catholic mathematician.He studied geometry with Monge at the École Polytechnique and then became a naval engineer. In 1819 he was appointed professor at the Conservatoire des Arts et Métiers; he kept this post until 1854...

.

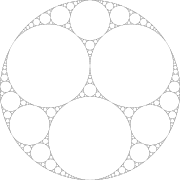
By solving Apollonius' problem repeatedly to find the inscribed circle, the interstices between mutually tangential circles can be filled arbitrarily finely, forming an Apollonian gasket

Apollonian gasket

, also known as a Leibniz packing or an Apollonian packing. This gasket is a fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

, being self-similar and having a dimension

Hausdorff dimension

thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...

d that is not known exactly but is roughly 1.3, which is higher than that of a regular (or rectifiable) curve (d = 1) but less than that of a plane (d = 2). The Apollonian gasket was first described by Gottfried Leibniz

Gottfried Leibniz

Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....

in the 17th century, and is a curved precursor of the 20th-century Sierpiński triangle

Sierpinski triangle

The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...

. The Apollonian gasket also has deep connections to other fields of mathematics; for example, it is the limit set of Kleinian group

Kleinian group

In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...

s.

The configuration of a circle tangent to four circles in the plane has special properties, which have been elucidated by Larmor (1891) and Lachlan (1893). Such a configuration is also the basis for Casey's theorem

Casey's theorem

In mathematics, Casey's theorem, also known as the generalized Ptolemy's theorem, is a theorem in Euclidean geometry named after the Irish mathematician John Casey.- Formulation of the theorem:...

, itself a generalization of Ptolemy's theorem

Ptolemy's theorem

In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...

.

The extension of Apollonius' problem to three dimensions, namely, the problem of finding a fifth sphere that is tangent to four given spheres, can be solved by analogous methods. For example, the given and solution spheres can be resized so that one given sphere is shrunk to point while maintaining tangency. Inversion in this point reduces Apollonius' problem to finding a plane that is tangent to three given spheres. There are in general eight such planes, which become the solutions to the original problem by reversing the inversion and the resizing. This problem was first considered by Pierre de Fermat

Pierre de Fermat

Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...

, and many alternative solution methods have been developed over the centuries.

Apollonius' problem can even be extended to d dimensions, to construct the hypersphere

Hypersphere

In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...

s tangent to a given set of hyperspheres. Following the publication of Frederick Soddy

Frederick Soddy

's re-derivation of the Descartes theorem in 1936, several people solved (independently) the mutually tangent case corresponding to Soddy's circles in d dimensions.

Applications

The principal application of Apollonius' problem, as formulated by Isaac Newton, is hyperbolic trilateration, which seeks to determine a position from the differences in distances to at least three points. For example, a ship may seek to determine its position from the differences in arrival times of signals from three synchronized transmitters. Solutions to Apollonius' problem were used in World War I

World War I

World War I , which was predominantly called the World War or the Great War from its occurrence until 1939, and the First World War or World War I thereafter, was a major war centred in Europe that began on 28 July 1914 and lasted until 11 November 1918...

to determine the location of an artillery piece from the time a gunshot was heard at three different positions, and hyperbolic trilateration is the principle used by the Decca Navigator System

Decca Navigator System

The Decca Navigator System was a low frequency hyperbolic navigation system that was first deployed during World War II when the Allied forces needed a system which could be used to achieve accurate landings...

and LORAN

LORAN

LORAN is a terrestrial radio navigation system using low frequency radio transmitters in multiple deployment to determine the location and speed of the receiver....

. Similarly, the location of an aircraft may be determined from the difference in arrival times of its transponder

Transponder (aviation)

A transponder is an electronic device that produces a response when it receives a radio-frequency interrogation...

signal at four receiving stations. This multilateration

Multilateration

Multilateration is a navigation technique based on the measurement of the difference in distance to two or more stations at known locations that broadcast signals at known times. Unlike measurements of absolute distance or angle, measuring the difference in distance results in an infinite number of...

problem is equivalent to the three dimensional generalization of Apollonius' problem and applies to global positioning systems such as GPS. It is also used to determine the position of calling animals (such as birds and whales), although Apollonius' problem does not pertain if the speed of sound

Speed of sound

The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....

varies with direction (i.e., the transmission medium

Transmission medium

A transmission medium is a material substance that can propagate energy waves...

not isotropic).

Apollonius' problem has other applications. In Book 1, Proposition 21 in his Principia, Isaac Newton

Isaac Newton

used his solution of Apollonius' problem to construct an orbit in celestial mechanics

Celestial mechanics

Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...

from the center of attraction and observations of tangent lines to the orbit corresponding to instantaneous velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

. The special case of the problem of Apollonius when all three circles are tangent is used in the Hardy–Littlewood circle method of analytic number theory

Analytic number theory

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...

to construct Hans Rademacher

Hans Rademacher

Hans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...

's contour for complex integration, given by the boundaries of an infinite set of Ford circle

Ford circle

In mathematics, a Ford circle is a circle with centre at and radius 1/, where p/q is an irreducible fraction, i.e. p and q are coprime integers...

s each of which touches several others. Finally, Apollonius' problem has been applied to some types of packing problem

Packing problem

Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...

s, which arise in disparate fields such as the error-correcting codes used on DVD

DVD

A DVD is an optical disc storage media format, invented and developed by Philips, Sony, Toshiba, and Panasonic in 1995. DVDs offer higher storage capacity than Compact Discs while having the same dimensions....

s and the design of pharmaceuticals that bind in a particular enzyme

Enzyme

Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...

of a pathogenic bacterium

Bacteria

Bacteria are a large domain of prokaryotic microorganisms. Typically a few micrometres in length, bacteria have a wide range of shapes, ranging from spheres to rods and spirals...

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Statement of the problem

History

Intersecting hyperbolas

Viète's reconstruction

Algebraic solutions

Lie sphere geometry

Inversive methods

Pairs of solutions by inversion

Inversion to an annulus

Resizing and inversion

Shrinking one given circle to a point

Resizing two given circles to tangency

Gergonne's solution

Ten combinations of points, circles, and lines

Number of solutions

Mutually tangent given circles: Soddy's circles and Descartes' theorem

Generalizations

Applications

Further reading

External links