
Riemann sphere
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riemann sphere (or extended complex plane), named after the 19th century mathematician Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, is the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
obtained from the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
by adding a point at infinity. The sphere is the geometric representation of the extended complex numbers
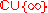 , which consist of the complex number
, which consist of the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s together with a symbol
 to represent infinity
to represent infinityInfinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
.
The extended complex numbers are useful in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
because they allow for division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
in some circumstances, in a way that makes expressions such as
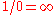
well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
. For example, any rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
on the complex plane can be extended to a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
can be thought of as a continuous function whose codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
is the Riemann sphere.
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Riemann sphere is the prototypical example of a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, and is one of the simplest complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s. In projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, the sphere can be thought of as the complex projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
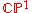 , the projective space
, the projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of all complex line
Complex line
In mathematics, a complex line is a one-dimensional affine subspace of a vector space over the complex numbers. A common point of confusion is that while a complex line has dimension one over C , it has dimension two over the real numbers R, and is topologically equivalent to a real plane, not a...
s in
 . As with any compact
. As with any compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemann surface, the sphere may also be viewed as a projective algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, making it a fundamental example in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. It also finds utility in other disciplines that depend on analysis and geometry, such as quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and other branches of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
Extended complex numbers
The extended complex numbers consist of the complex numbers together with
together with  . The extended complex numbers may be written as
. The extended complex numbers may be written as 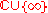 , and are often denoted by adding some decoration to the letter
, and are often denoted by adding some decoration to the letter  , such as
, such as
Geometrically, the set of extended complex numbers is referred to as the Riemann sphere (or extended complex plane).
Arithmetic operations
AdditionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
of complex numbers may be extended by defining

for any complex number
 , and multiplication
, and multiplicationMultiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
may be defined by

for all nonzero complex numbers
 , with
, with  . Note that
. Note that  and
and  are left undefined. Unlike the complex numbers, the extended complex numbers do not form a field
are left undefined. Unlike the complex numbers, the extended complex numbers do not form a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, since
 does not have a multiplicative inverse
does not have a multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
. Nonetheless, it is customary to define division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
on
 by
by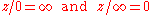
for all nonzero complex numbers
 , with
, with  and
and  .
.Rational functions
Any rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
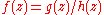 can be extended to a continuous function
can be extended to a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the Riemann sphere. Specifically, if
 is a complex number such that the denominator
is a complex number such that the denominator 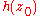 is zero but the numerator
is zero but the numerator 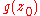 is nonzero, then
is nonzero, then 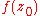 can be defined as
can be defined as  . (If both the numerator and denominator are zero, then they share a common factor, and the fraction should first be reduced to lowest terms.) Moreover,
. (If both the numerator and denominator are zero, then they share a common factor, and the fraction should first be reduced to lowest terms.) Moreover, 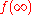 can be defined as the limit
can be defined as the limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of
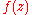 as
as  , which may be finite or infinite.
, which may be finite or infinite.For example, given the function
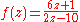
we may define
 since the denominator is zero at
since the denominator is zero at  , and
, and  since
since 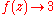 as
as  . Using these definitions,
. Using these definitions,  becomes a continuous function from the Riemann sphere to itself.
becomes a continuous function from the Riemann sphere to itself.When viewed as a complex manifold, these rational functions are in fact holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s from the Riemann sphere to itself.
As a complex manifold
As a one-dimensional complex manifold, the Riemann sphere can be described by two charts, both with domain equal to the complex number plane . Let
. Let  and
and 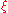 be complex coordinates on
be complex coordinates on  . Identify the nonzero complex numbers
. Identify the nonzero complex numbers  with the nonzero complex numbers
with the nonzero complex numbers  using the transition maps
using the transition maps
Since the transition maps are holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, they define a complex manifold, called the Riemann sphere.
Intuitively, the transition maps indicate how to glue two planes together to form the Riemann sphere. The planes are glued in an "inside-out" manner, so that they overlap almost everywhere, with each plane contributing just one point (its origin) missing from the other plane. In other words, (almost) every point in the Riemann sphere has both a
 value and a
value and a 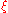 value, and the two values are related by
value, and the two values are related by 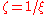 . The point where
. The point where  should then have
should then have  -value "
-value " "; in this sense, the origin of the
"; in this sense, the origin of the  -chart plays the role of "
-chart plays the role of " " in the
" in the  -chart. Symmetrically, the origin of the
-chart. Symmetrically, the origin of the  -chart plays the role of
-chart plays the role of  in the
in the  -chart.
-chart.Topologically
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the resulting space is the one-point compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of a plane into the sphere. However, the Riemann sphere is not merely a topological sphere. It is a sphere with a well-defined complex structure, so that around every point on the sphere there is a neighborhood that can be biholomorphically identified with
 .
.On the other hand, the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
, a central result in the classification of Riemann surfaces, states that the only simply-connected one-dimensional complex manifolds are the complex plane, the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, and the Riemann sphere. Of these, the Riemann sphere is the only one that is a closed surface
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
(a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
surface without boundary). Hence the two-dimensional sphere admits a unique complex structure turning it into a one-dimensional complex manifold.
As the complex projective line
The Riemann sphere can also be defined as the complex projective line. This is the subset of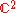 consisting of all pairs
consisting of all pairs 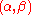 of complex numbers, not both zero, modulo the equivalence relation
of complex numbers, not both zero, modulo the equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
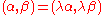
for all nonzero complex numbers
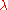 . The complex plane
. The complex plane  , with coordinate
, with coordinate  , can be mapped into the complex projective line by
, can be mapped into the complex projective line by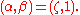
Another copy of
 with coordinate
with coordinate 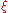 can be mapped in by
can be mapped in by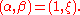
These two complex charts cover the projective line. For nonzero
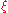 the identifications
the identifications
demonstrate that the transition maps are
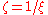 and
and 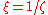 , as above.
, as above.This treatment of the Riemann sphere connects most readily to projective geometry. For example, any line (or smooth conic) in the complex projective plane is biholomorphic to the complex projective line. It is also convenient for studying the sphere's automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s, later in this article.
As a sphere
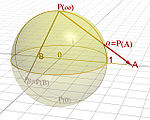
 in the three-dimensional real space
in the three-dimensional real space  . To this end, consider the stereographic projection
. To this end, consider the stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
from the unit sphere minus the point
 onto the plane
onto the plane  , which we identify with the complex plane by
, which we identify with the complex plane by  . In Cartesian coordinates
. In Cartesian coordinates 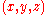 and spherical coordinates
and spherical coordinates  on the sphere (with
on the sphere (with  the zenith and
the zenith and  the azimuth), the projection is
the azimuth), the projection is
Similarly, stereographic projection from
 onto the
onto the  plane, identified with another copy of the complex plane by
plane, identified with another copy of the complex plane by  , is written
, is written
In order to cover the unit sphere, one needs the two stereographic projections: the first will cover the whole sphere except the point (0,0,1) and the second except the point (0,0,-1). Hence, one needs two complex planes, one for each projection, which can be intuitively seen as glued back-to-back at z=0. Note that the two complex planes are identified differently with the plane
 . An orientation
. An orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-reversal is necessary to maintain consistent orientation on the sphere, and in particular complex conjugation causes the transition maps to be holomorphic.
The transition maps between
 -coordinates and
-coordinates and 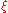 -coordinates are obtained by composing one projection with the inverse of the other. They turn out to be
-coordinates are obtained by composing one projection with the inverse of the other. They turn out to be 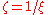 and
and 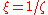 , as described above. Thus the unit sphere is diffeomorphic
, as described above. Thus the unit sphere is diffeomorphicDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to the Riemann sphere.
Under this diffeomorphism, the unit circle in the
 -chart, the unit circle in the
-chart, the unit circle in the 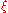 -chart, and the equator of the unit sphere are all identified. The unit disk
-chart, and the equator of the unit sphere are all identified. The unit disk  is identified with the southern hemisphere
is identified with the southern hemisphere  , while the unit disk
, while the unit disk  is identified with the northern hemisphere
is identified with the northern hemisphere  .
.Metric
A Riemann surface does not come equipped with any particular Riemannian metric. However, the complex structure of the Riemann surface does uniquely determine a metric up to conformal equivalenceConformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
. (Two metrics are said to be conformally equivalent if they differ by multiplication by a positive smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
.) Conversely, any metric on an oriented surface uniquely determines a complex structure, which depends on the metric only up to conformal equivalence. Complex structures on an oriented surface are therefore in one-to-one correspondence with conformal classes of metrics on that surface.
Within a given conformal class, one can use conformal symmetry to find a representative metric with convenient properties. In particular, there is always a complete metric with constant curvature
Constant curvature
In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...
in any given conformal class.
In the case of the Riemann sphere, the Gauss-Bonnet theorem implies that a constant-curvature metric must have positive curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
K. It follows that the metric must be isometric
Isometry (Riemannian geometry)
In the study of Riemannian geometry in mathematics, a local isometry from one Riemannian manifold to another is a map which pulls back the metric tensor on the second manifold to the metric tensor on the first...
to the sphere of radius
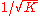 in
in 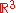 via stereographic projection. In the
via stereographic projection. In the  -chart on the Riemann sphere, the metric with
-chart on the Riemann sphere, the metric with  is given by
is given by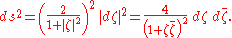
In real coordinates
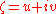 , the formula is
, the formula is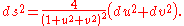
Up to a constant factor, this metric agrees with the standard Fubini–Study metric on complex projective space (of which the Riemann sphere is an example).
Conversely, let S denote the sphere (as an abstract smooth
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
or topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
). By the uniformization theorem there exists a unique complex structure on S. It follows that any metric on S is conformally equivalent to the round metric. All such metrics determine the same conformal geometry. The round metric is therefore not intrinsic to the Riemann sphere, since "roundness" is not an invariant of conformal geometry. The Riemann sphere is only a conformal manifold, not a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. However, if one needs to do Riemannian geometry on the Riemann sphere, the round metric is a natural choice.
Automorphisms

The study of any mathematical object is aided by an understanding of its group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of automorphisms, meaning the maps from the object to itself that preserve the essential structure of the object. In the case of the Riemann sphere, an automorphism is an invertible biholomorphic map from the Riemann sphere to itself. It turns out that the only such maps are the Möbius transformations. These are functions of the form
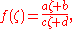
where
 ,
,  ,
,  , and
, and 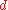 are complex numbers such that
are complex numbers such that  . Examples of Möbius transformations include dilation
. Examples of Möbius transformations include dilationDilation
Dilation refers to an enlargement or expansion in bulk or extent, the opposite of contraction. It derives from the Latin dilatare, "to spread wide".In physiology:* Pupillary dilation, dilation of the pupil of the eye...
s, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s, translations, and complex inversion. In fact, any Möbius transformation can be written as a composition of these.
The Möbius transformations are profitably viewed as transformations on the complex projective line. In projective coordinates, the transformation
 can be written
can be written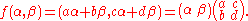
Thus the Möbius transformations can be described as
 complex matrices with nonzero determinant
complex matrices with nonzero determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
; two matrices yield the same Möbius transformation if and only if they differ by a nonzero factor. Thus the Möbius transformations exactly correspond to the projective linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s
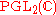 .
.If one endows the Riemann sphere with the Fubini–Study metric, then not all Möbius transformations are isometries; for example, the dilations and translations are not. The isometries form a proper subgroup of
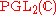 , namely
, namely 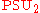 . This subgroup is isomorphic to the rotation group
. This subgroup is isomorphic to the rotation groupRotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
 , which is the group of symmetries of the unit sphere in
, which is the group of symmetries of the unit sphere in  (which, when restricted to the sphere, become the isometries of the sphere).
(which, when restricted to the sphere, become the isometries of the sphere).Applications
In complex analysis, a meromorphic function on the complex plane (or on any Riemann surface, for that matter) is a ratio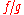 of two holomorphic functions
of two holomorphic functions  and
and 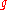 . As a map to the complex numbers, it is undefined wherever
. As a map to the complex numbers, it is undefined wherever  is zero. However, it induces a holomorphic map
is zero. However, it induces a holomorphic map 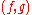 to the complex projective line that is well-defined even where
to the complex projective line that is well-defined even where  . This construction is helpful in the study of holomorphic and meromorphic functions. For example, on a compact Riemann surface there are no non-constant holomorphic maps to the complex numbers, but holomorphic maps to the complex projective line are abundant.
. This construction is helpful in the study of holomorphic and meromorphic functions. For example, on a compact Riemann surface there are no non-constant holomorphic maps to the complex numbers, but holomorphic maps to the complex projective line are abundant.The Riemann sphere has many uses in physics. In quantum mechanics, points on the complex projective line are natural values for photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
polarization
Photon polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
states, spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
states of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
ive particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
s of spin 1/2, and 2-state particles in general. The Riemann sphere has been suggested as a relativistic
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
model for the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
. In string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the worldsheet
Worldsheet
In string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind around 1967 as a direct generalization of the world line concept for a point particle in special and general relativity.The type of string,...
s of strings are Riemann surfaces, and the Riemann sphere, being the simplest Riemann surface, plays a significant role. It is also important in twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
.
See also
- Conformal geometryConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
- Cross-ratioCross-ratioIn geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
- Hopf bundleHopf bundleIn the mathematical field of topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle...
- Dessin d'enfantDessin d'enfantIn mathematics, a dessin d'enfant is a type of graph drawing used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers.Intuitively, a dessin d'enfant is simply a graph, with its vertices colored alternating black and...
- Directed infinityDirected infinityA directed infinity is a type of infinity in the complex plane that has a defined angle θ but an infinite absolute value r. For example, the limit of 1/x where x is a positive number approaching zero is a directed infinity with angle 0; however, 1/0 is not a directed infinity, but a complex infinity...
External links
- Moebius Transformations Revealed, by Douglas N. ArnoldDouglas N. ArnoldDouglas Norman Arnold is a mathematician whose research focuses on the numerical analysis of partial differential equations with applications in mechanics and other fields in physics. , he is McKnight Presidential Professor of Mathematics at the University of Minnesota.Arnold studied mathematics as...
and Jonathan Rogness (a video by two University of Minnesota professors explaining and illustrating Möbius transformations using stereographic projection from a sphere)

