
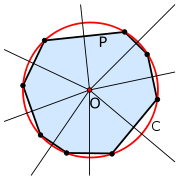
Circumscribed circle
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the circumscribed circle or circumcircle of a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
which passes through all the vertices of the polygon. The center of this circle is called the circumcenter.
A polygon which has a circumscribed circle is called a cyclic polygon. All regular
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
s, all triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and all rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s are cyclic.
A related notion is the one of a minimum bounding circle
Smallest circle problem
The smallest circle problem or minimum covering circle problem is a mathematical problem of computing the smallest circle that contains all of a given set of points in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere problem, is to compute the...
, which is the smallest circle that completely contains the polygon within it. Not every polygon has a circumscribed circle, as the vertices of a polygon do not need to all lie on a circle, but every polygon has a unique minimum bounding circle, which may be constructed by a linear time algorithm. Even if a polygon has a circumscribed circle, it may not coincide with its minimum bounding circle; for example, for an obtuse triangle, the minimum bounding circle has the longest side as diameter and does not pass through the opposite vertex.
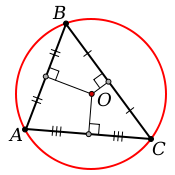
Circumscribed circles of triangles
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is

Since this equation has three parameters (a, b, r) only three pairs of points are required to determine the equation of a circle. Since a triangle is defined by its three vertexes, and exactly three points are required to determine a circle, every triangle can be circumscribed.
The circumcenter of a triangle can be found as the intersection of any two of the three perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
bisector
Bisection
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...
s. (A perpendicular bisector is a line that forms a right angle with one of the triangle's sides and intersects that side at its midpoint
Midpoint
The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
.) This is because the circumcenter is equidistant from any pair of the triangle's vertices, and all points on the perpendicular bisectors are equidistant from two of the vertices of the triangle.
Alternate method to determine the circumcenter: draw any two lines departing the vertices at an angle with the common side, equal to 90 degrees minus the angle of the opposite vertex.
In coastal navigation
Pilotage
Pilotage is the use of fixed visual references on the ground or sea by means of sight or radar to guide oneself to a destination, sometimes with the help of a map or nautical chart. People use pilotage for activities such as guiding vessels and aircraft, hiking and Scuba diving...
, a triangle's circumcircle is sometimes used as a way of obtaining a position line
Position line
A position line is a line that can be identified both on a nautical chart or aeronautical chart and by observation out on the surface of the earth...
using a sextant
Sextant
A sextant is an instrument used to measure the angle between any two visible objects. Its primary use is to determine the angle between a celestial object and the horizon which is known as the altitude. Making this measurement is known as sighting the object, shooting the object, or taking a sight...
when no compass
Compass
A compass is a navigational instrument that shows directions in a frame of reference that is stationary relative to the surface of the earth. The frame of reference defines the four cardinal directions – north, south, east, and west. Intermediate directions are also defined...
is available. The horizontal angle between two landmarks defines the circumcircle upon which the observer lies.
The circumcenter's position depends on the type of triangle:
- If and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a triangle is acute (all angles smaller than a right angle), the circumcenter lies inside the triangle - If and only if it is obtuse (has one angle bigger than a right angle), the circumcenter lies outside
- If and only if it is a right triangle, the circumcenter lies at the center of the hypotenuseHypotenuseIn geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
. This is one form of Thales' theoremThales' theoremIn geometry, Thales' theorem states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem...
.
The diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the circumcircle can be computed as the length of any side of the triangle, divided by the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of the opposite angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
. (As a consequence of the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
, it does not matter which side is taken: the result will be the same.) The triangle's nine-point circle
Nine-point circle
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
has half the diameter of the circumcircle. The diameter of the circumcircle of the triangle ΔABC is
-

where a, b, c are the lengths of the sides of the triangle and s = (a + b + c)/2 is the semiperimeter. The expression above is the area of the triangle, by Heron's formula. Trigometric expressions for the diameter of the circumcircle include
above is the area of the triangle, by Heron's formula. Trigometric expressions for the diameter of the circumcircle include

In any given triangle, the circumcenter is always collinear with the centroidCentroidIn geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
and orthocenter. The line that passes through all of them is known as the Euler line.
The isogonal conjugateIsogonal conjugateIn geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C. These three reflected lines concur at the isogonal conjugate of P...
of the circumcenter is the orthocenter.
The useful minimum bounding circleSmallest circle problemThe smallest circle problem or minimum covering circle problem is a mathematical problem of computing the smallest circle that contains all of a given set of points in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere problem, is to compute the...
of three points is defined either by the circumcircle (where three points are on the minimum bounding circle) or by the two points of the longest side of the triangle (where the two points define a diameter of the circle). It is common to confuse the minimum bounding circle with the circumcircle.
The circumcircle of three collinear points is the line on which the three points lie, often referred to as a circle of infinite radius. Nearly collinear points often lead to numerical instability in computation of the circumcircle.
Circumcircles of triangles have an intimate relationship with the Delaunay triangulationDelaunay triangulationIn mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
of a set of points.
Circumcircle equations
In the Euclidean plane, it is possible to give explicitly an equation of the circumcircle in terms of the Cartesian coordinates of the vertices of the inscribed triangle. Thus suppose that



are the coordinates of points A, B, and C. The circumcircle is then the locus of points v = (vx,vy) in the Cartesian plane satisfying the equations




guaranteeing that the points A, B, C, and v are all the same distance r from the common center u of the circle. Using the polarization identityPolarization identityIn mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
, these equations reduce to the condition that the matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

have a nonzero kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
. Thus the circumcircle may alternatively be described as the locus of zeros of the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of this matrix:

Expanding by cofactor expansion, let


we then have a|v|2 − 2Sv − b = 0 and, assuming the three points were not in a line (otherwise the circumcircle is that line that can also be seen as a generalized circle with S at infinity), |v − S/a|2 = b/a + |S|2/a2, giving the circumcenter S/a and the circumradius √ (b/a + |S|2/a2). A similar approach allows one to deduce the equation of the circumsphere of a tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
.
An equation for the circumcircle in trilinear coordinatesTrilinear coordinatesIn geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
x : y : z is a/x + b/y + c/z = 0. An equation for the circumcircle in barycentric coordinatesBarycentric coordinates (mathematics)In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
x : y : z is a2/x + b2/y + c2/z = 0.
The isogonal conjugateIsogonal conjugateIn geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C. These three reflected lines concur at the isogonal conjugate of P...
of the circumcircle is the line at infinity, given in trilinear coordinatesTrilinear coordinatesIn geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
by ax + by + cz = 0 and in barycentric coordinates by x + y + z = 0.
Additionally, the circumcircle of a triangle embedded in d dimensions can be found using a generalized method. Let A, B, and C be d-dimensional points, which form the vertices of a triangle. We start by transposing the system to place C at the origin:

Case of three dimensions:
The circumradius, r, is then
where θ is the interior angle between a and b. The circumcenter, p0, is given by
These formulas can be used directly in the three dimensions only because the cross product is not defined as binary operation otherwise, but these formulas can be easy extended to the d dimensions case using following identities valid for arbitrary vectors in three dimensions:



Cartesian coordinates
The Cartesian coordinates of the circumcenter are


with
Without loss of generality this can be expressed in a simplified form after translation of the vertex A to the origin of the Cartesian coordinate systems, i.e., when . In this case, the coordinates of the vertices B' = B − A and C' = C − A represent the vectors from vertex A' to these vertices. Observe that this trivial translation is possible for all triangles and the circumcenter coordinates of the triangle A'B'C' follow as
. In this case, the coordinates of the vertices B' = B − A and C' = C − A represent the vectors from vertex A' to these vertices. Observe that this trivial translation is possible for all triangles and the circumcenter coordinates of the triangle A'B'C' follow as
with
Barycentric coordinates as a function of the side lengths
The circumcenter has trilinear coordinatesTrilinear coordinatesIn geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
(cos α, cos β, cos γ) where α, β, γ are the angles of the triangle. The circumcenter has barycentric coordinatesBarycentric coordinates (mathematics)In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
where a, b, c are edge lengths (BC, CA, AB respectively) of the triangle.
Barycentric coordinates from cross- and dot-products
In Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, there is a unique circle passing through any given three non-collinear points P1, P2, and P3. Using Cartesian coordinates to represent these points as spatial vectors, it is possible to use the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
to calculate the radius and center of the circle. Let

Then the radius of the circle is given by

The center of the circle is given by the linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

where



Parametric equation of a triangle's circumcircle
A unit vector perpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the plane containing the circle is given by

Hence, given the radius, r, center, Pc, a point on the circle, P0 and a unit normal of the plane containing the circle, , one parametric equation of the circle starting from the point P0 and proceeding in a positively oriented (i.e., right-handedRight-hand ruleIn mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
, one parametric equation of the circle starting from the point P0 and proceeding in a positively oriented (i.e., right-handedRight-hand ruleIn mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
) sense about is the following:
is the following:

The angles which the circle forms with a triangle's sides
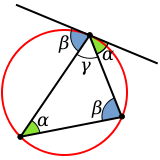
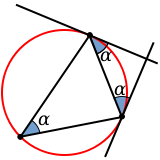
The angles which the circumscribed circle forms with the sides of the triangle coincide with angles at which sides meet each other. The side opposite angle α meets the circle twice: once at each end; in each case at angle α (similarly for the other two angles). The alternate segment theorem states that the angle between the tangent and chord equals the angle in the alternate segment.
Triangle centers on the circumcircle of triangle ABC
In this section, the vertex angles are labeled A, B, C and all coordinates are trilinear coordinatesTrilinear coordinatesIn geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
:
- Steiner point = bc/ (b2 − c2) : ca/ (c2 − a2) : ab/(a2 − b2) = the nonvertex point of intersection of the circumcircle with the Steiner ellipse. (The Steiner ellipse, with center = centroid(ABC), is the ellipse of least area that passes through A, B, and C. An equation for this ellipse is 1/(ax) + 1/(by) + 1/(cz) = 0.)
- Tarry pointTarry pointIn geometry, the Tarry point for a triangle is a point of concurrency of the lines through the vertices of the triangle perpendicular to the corresponding sides of the triangle's first Brocard triangle. The Tarry point lies on the other endpoint of the diameter of the circumcircle drawn through...
= sec (A + ω) : sec (B + ω) : sec (C + ω) = antipode of the Steiner point
- Focus of the Kiepert parabola = csc (B − C) : csc (C − A) : csc (A − B).
Other properties of the circumcircle of a triangle
The circumcircle radius is no smaller than twice the incircle radius (Euler's triangle inequality).
The distance between the circumcenter and the incenter is where r is the incircle radius and R is the circumcircle radius.
where r is the incircle radius and R is the circumcircle radius.
The product of the incircle radius and the circumcircle radius of a triangle with sides a, b, and c is
Cyclic quadrilaterals
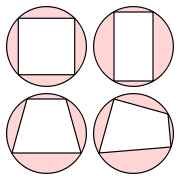
Quadrilaterals that can be circumscribed have particular properties including the fact that opposite angles are supplementary anglesSupplementary anglesSupplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....
(adding up to 180° or π radians).
Cyclic n-gons
For a cyclic polygon with an odd number of sides, all angles are equal if and only if the polygon is regular. A cyclic polygon with an even number of sides has all angles equal if and only if the alternate sides are equal (that is, sides 1, 3, 5, ... are equal, and sides 2, 4, 6, ... are equal).
See also
- Inscribed circle
- Jung's theoremJung's theoremIn geometry, Jung's theorem is an inequality between the diameter of a set of points in any Euclidean space and the radius of the minimum enclosing ball of that set...
, an inequality relating the diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of a point set to the radius of its minimum bounding circle - Lester's theoremLester's theoremIn Euclidean plane geometry, Lester's theorem, named after June Lester, states that in any scalene triangle, the two Fermat points, the nine-point center, and the circumcenter are concyclic.- References :...
- Circumscribed sphereCircumscribed sphereIn geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing...
- Triangle centerTriangle centerIn geometry a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of...
- Japanese theorem for cyclic quadrilaterals
- Japanese theorem for cyclic polygons
External links
- Derivation of formula for radius of circumcircle of triangle at Mathalino.com
Interactive
- Triangle circumcircle and circumcenter With interactive animation
- An interactive Java applet for the circumcenter
-






