This article discusses a family of circles sharing a radical axis

Radical axis

The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...

, and the corresponding family of orthogonal circles. For other circles associated with Apollonius of Perga

Apollonius of Perga

Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...

, please see the disambiguation page, circles of Apollonius

Circles of Apollonius

The term circle of Apollonius is used to describe several types of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a...

.

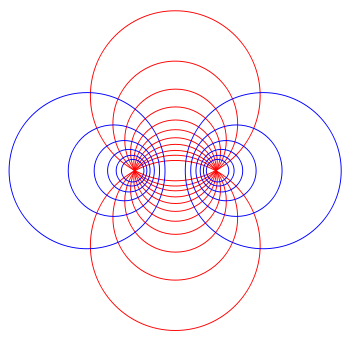
Apollonian circles are two families of circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

s such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates

Bipolar coordinates

Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...

. They were discovered by Apollonius of Perga

Apollonius of Perga

Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...

, a renowned Greek

Ancient Greece

Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...

 geometer.

Definition

The Apollonian circles are defined in two different ways by a line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

 denoted CD.

Each circle in the first family (the blue circles in the figure) is associated with a positive real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 r, and is defined as the locus of points X such that the ratio of distances from X to C and to D equals r,
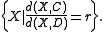
For values of r close to zero, the corresponding circle is close to C, while for values of r close to ∞, the corresponding circle is close to D; for the intermediate value r = 1, the circle degenerates to a line, the perpendicular bisector of CD. The equation defining these circles as a locus can be generalized to define the Fermat–Apollonius circles of larger sets of weighted points.

Each circle in the second family (the red circles in the figure) is associated with an angle θ, and is defined as the locus of points X such that the inscribed angle

Inscribed angle

In geometry, an inscribed angle is formed when two secant lines of a circle intersect on the circle....

 CXD equals θ,

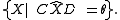
Scanning θ from 0 to π generates the set of all circles passing through the two points C and D.

Pencils of circles

Both of the families of Apollonian circles are called pencils of circles. More generally, there is a natural correspondence between circles in the plane and points in three-dimensional projective space

Projective space

In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....

; a line in this space corresponds to a one-dimensional continuous family of circles called a pencil.

Specifically, the equation of a circle of radius r centered at a point (p,q),
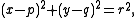
may be rewritten as
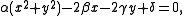
where α = 1, β = p, γ = q, and δ = p² + q² − r². However,
in this form, multiplying the 4-tuple (α,β,γ,δ) by a scalar

Scalar (mathematics)

In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....

 produces a different four-tuple that represents the same circle; thus, these 4-tuples may be considered to be homogeneous coordinates

Homogeneous coordinates

In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

 for the space of circles. Straight lines may also be represented with an equation of this type in which α = 0 and should be thought of as being a degenerate form of a circle. When α ≠ 0, we may solve for p = β/α, q = γ/α, and r =√((−δ − β² − γ²)/α²); note, however, that the latter formula may give r = 0 (in which case the circle degenerates to a point) or r equal to an imaginary number

Imaginary number

An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...

 (in which case the 4-tuple (α,β,γ,δ) is said to represent an imaginary circle).

The set of affine combinations of two circles (α₁,β₁,γ₁,δ₁), (α₂,β₂,γ₂,δ₂), that is, the set of circles represented by the four-tuple
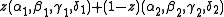
for some value of the parameter z,
forms a pencil; the two circles are called generators of the pencil. There are three types of pencil:

• An elliptic pencil (red family of circles in the figure) is defined by two generators that pass through each other in exactly two points (C and D). At these points, the defining formula has zero value, and therefore will also equal zero for any affine combination. Thus, every circle of an elliptic pencil passes through the same two points. An elliptic pencil does not include any imaginary circles.
• A hyperbolic pencil (blue family of circles in the figure) is defined by two generators that do not intersect each other at any point. It includes real circles, imaginary circles, and two degenerate point circles (here C and D) called the Poncelet points of the pencil. Each point in the plane belongs to exactly one circle of the pencil. forms a pencil of this type.
• Finally, a parabolic pencil (as a limiting case) is defined where two generating circles are tangent to each other at a single point . It consists of a family of real circles, all tangent to each other at a single common point. The degenerate circle with radius zero at that point also belongs to the pencil.

A family of concentric circles centered at a single focus C forms a special case of a hyperbolic pencil, in which the other focus is the point at infinity of the complex projective line. The corresponding elliptic pencil consists of the family of straight lines through C; these should be interpreted as circles that all pass through the point at infinity.

Radical axis and central line

Except for the two special cases of a pencil of concentric circles and a pencil of coincident lines,
any two circles within a pencil have the same radical axis

Radical axis

The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...

, and all circles in the pencil have collinear centers. Any three or more circles from the same family are called coaxal circles or coaxial circles.

The elliptic pencil of circles passing through the two points C and D (the set of red circles, in the figure) has the line CD as its radical axis. The centers of the circles in this pencil lie on the perpendicular bisector of CD.
The hyperbolic pencil defined by points C and D (the blue circles) has its radical axis on the perpendicular bisector of line CD, and all its circle centers on line CD.

The radical axis of any pencil of circles, interpreted as an infinite-radius circle, belongs to the pencil.
Any three circles belong to a common pencil whenever all three pairs share the same radical axis and their centers are collinear.

Inversive geometry, orthogonal intersection, and coordinate systems

Circle inversion transforms the plane in a way that maps circles into circles, and pencils of circles into pencils of circles. The type of the pencil is preserved: the inversion of an elliptic pencil is another elliptic pencil, the inversion of a hyperbolic pencil is another hyperbolic pencil, and the inversion of a parabolic pencil is another parabolic pencil.

It is relatively easy to show using inversion that, in the Apollonian circles, every blue circle intersects every red circle orthogonally, i.e., at a right angle

Right angle

In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

. Inversion of the blue Apollonian circles with respect to a circle centered on point C results in a pencil of concentric circles centered at the image of point D. The same inversion transforms the red circles into a set of straight lines that all contain the image of D. Thus, this inversion transforms the bipolar coordinate system

Bipolar coordinates

Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...

 defined by the Apollonian circles into a polar coordinate system.
Obviously, the transformed pencils meet at right angles. Since inversion is a conformal transformation

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

, it preserves the angles between the curves it transforms, so the original Apollonian circles also meet at right angles.

Alternatively, the orthogonal property of the two pencils follows from the defining property of the radical axis, that from any point X on the radical axis of a pencil P the lengths of the tangents from X to each circle in P are all equal. It follows from this that the circle centered at X with length equal to these tangents crosses all circles of P perpendicularly. The same construction can be applied for each X on the radical axis of P, forming another pencil of circles perpendicular to P.

More generally, for every pencil of circles there exists a unique pencil consisting of the circles that are perpendicular to the first pencil. If one pencil is elliptic, its perpendicular pencil is hyperbolic, and vice versa; in this case the two pencils form a set of Apollonian circles. The pencil of circles perpendicular to a parabolic pencil is also parabolic; it consists of the circles that have the same common tangent point but with a perpendicular tangent line at that point.